IF p q r s are in harmonic progression and p>s then
1ps<1qr
q+r=p+s
1q+19=1r+1s
none
The correct Answer is:D
To solve the problem, we need to analyze the condition given that p,q,r,s are in harmonic progression (HP) and p>s.
1. Understanding Harmonic Progression:
- If p,q,r,s are in HP, then their reciprocals 1p,1q,1r,1s are in arithmetic progression (AP).
2. Setting Up the AP Condition:
- For four terms in AP, the condition can be expressed as:
2⋅(middle term)=(first term)+(last term)
- In our case, we can express this as:
1/q−1/p=1/s−1/r
3. Rearranging the Equation:
- We can rearrange the terms:
1q+1r=1s+1p
4. Interpreting the Condition:
- This equation indicates a relationship between the reciprocals of p,q,r, and s. Since p>s, we can infer that the relationship must hold true under this condition.
5. Conclusion:
- The derived condition 1q+1r=1s+1p is the final result we were looking for.
Final Result:
Thus, the condition that holds true if p,q,r,s are in harmonic progression and p>s is:
1q+1r=1s+1p
- If p,q,r,s are in HP, then their reciprocals 1p,1q,1r,1s are in arithmetic progression (AP).
- For four terms in AP, the condition can be expressed as:
2⋅(middle term)=(first term)+(last term)
- In our case, we can express this as:
1/q−1/p=1/s−1/r
- We can rearrange the terms:
1q+1r=1s+1p
- This equation indicates a relationship between the reciprocals of p,q,r, and s. Since p>s, we can infer that the relationship must hold true under this condition.
- The derived condition 1q+1r=1s+1p is the final result we were looking for.
Thus, the condition that holds true if p,q,r,s are in harmonic progression and p>s is:
1q+1r=1s+1p
Topper's Solved these Questions
- SEQUENCE AND SERIES Book:KIRAN PUBLICATIONChapter:SEQUENCE AND SERIES Exercise:TYPE V
Explore 19 Videos
- RATIO AND PROPORTION Book:KIRAN PUBLICATIONChapter:RATIO AND PROPORTION Exercise:TEST YOURSELF
Explore 19 Videos
- SIMPLE INTERSETBook:KIRAN PUBLICATIONChapter:SIMPLE INTERSETExercise:TEST YOURSELF
Explore 25 Videos
Similar Questions
Knowledge Check
If P=(1xp,p),Q=(1xq,q),R=(1xr,r) where xk≠0,k=p,q,r≠N , denotes the kth term of a Harmonic progression , then
AArea (ΔPQR)=p2q2r22√(p−q)2+(q−r)2+(r−p)2BΔPQR is a right angled triangleCthe points P,Q and R are collinearDnone of theseGiven that 0 < p < q < r < s and p, q, r, s are integers, which of the following is the smallest?
Ap+qr+sBp+sq+rCq+sp+rDr+sp+qLet a:~(p∧~r)∨(~q∨s)andb:(p∨s)lar(q∧r). If the truth values of p and q are true and that of r and s are false, then the truth values of a and b are respectively . . .
AF,FBT,TCT,FDF,T
In Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
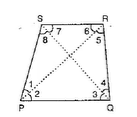
View SolutionIn Figure, PQR is a triangle and S is any point in its interior, show that SQ+SR<PQ+PR Given : S is any point in the interior of PQR To Prove : SQ+SR<PQ+PR Construction: Produce QS to meet PR in T
View SolutionIf the sequence {Sn} is a geometric progression and S2S11=SpS8, then what is the value of p?
View SolutionP is processed in industries to get some useful products such as Q, R and S. S is obtained during the processing of P to get Q, R is a mixture of about 200 substances. Identify P, Q, R and S.
View SolutionIf p,q,r and s are positive real numbers such that p+q+r+s=2, then M=(p+q)(r+s) satisfies the relation, when (A) 0<M≤1 (B) 1≤M≤2 .(C) 2≤M≤3 (D) 3≤M≤4
View Solution