A cylindrical jar without a lid has to be constructed using a given surface area of a metal sheet It the capacity of the jar is to maximum, then the diameter of the jar must be k times the height of the jar The value of k is:
1
2
3
4
The correct Answer is:B
To solve the problem of maximizing the capacity of a cylindrical jar without a lid, we will follow these steps:
Step 1: Understand the Surface Area and Volume Formulas
For a cylindrical jar without a lid, the surface area S and volume V can be expressed as:
- Surface Area: S=2πrh+πr2 (where r is the radius and h is the height)
- Volume: V=πr2h
Step 2: Relate Diameter and Height
According to the problem, the diameter D of the jar is k times the height h. Since the diameter is twice the radius, we have:
D=2r=k⋅h
From this, we can express the radius in terms of height:
r=kh2
Step 3: Substitute for Height in the Surface Area Formula
We can substitute r in the surface area formula. First, we need to express h in terms of r:
From the surface area formula:
S=2πrh+πr2
Rearranging gives us:
h=S−πr22πr
Step 4: Substitute h in the Volume Formula
Now, we substitute h back into the volume formula:
V=πr2(S−πr22πr)
This simplifies to:
V=r(S−πr2)2
Step 5: Differentiate the Volume with Respect to r
To find the maximum volume, we differentiate V with respect to r:
dVdr=ddr(Sr2−πr32)
This gives us:
dVdr=S2−3πr22
Step 6: Set the Derivative Equal to Zero
To find the critical points, set the derivative equal to zero:
S2−3πr22=0
This leads to:
S=3πr2
Step 7: Substitute Back to Find h
Now, substitute S back into the equation for h:
Using S=3πr2:
h=3πr22πr−r2
This simplifies to:
h=3r2−r2=r
Step 8: Relate Diameter to Height
Since h=r, we can now express the diameter:
D=2r=2h
Thus, we can conclude:
k=2
Final Answer
The value of k is 2.
---
For a cylindrical jar without a lid, the surface area S and volume V can be expressed as:
- Surface Area: S=2πrh+πr2 (where r is the radius and h is the height)
- Volume: V=πr2h
According to the problem, the diameter D of the jar is k times the height h. Since the diameter is twice the radius, we have:
D=2r=k⋅h
From this, we can express the radius in terms of height:
r=kh2
We can substitute r in the surface area formula. First, we need to express h in terms of r:
From the surface area formula:
S=2πrh+πr2
Rearranging gives us:
h=S−πr22πr
Now, we substitute h back into the volume formula:
V=πr2(S−πr22πr)
This simplifies to:
V=r(S−πr2)2
To find the maximum volume, we differentiate V with respect to r:
dVdr=ddr(Sr2−πr32)
This gives us:
dVdr=S2−3πr22
To find the critical points, set the derivative equal to zero:
S2−3πr22=0
This leads to:
S=3πr2
Now, substitute S back into the equation for h:
Using S=3πr2:
h=3πr22πr−r2
This simplifies to:
h=3r2−r2=r
Since h=r, we can now express the diameter:
D=2r=2h
Thus, we can conclude:
k=2
The value of k is 2.
Topper's Solved these Questions
- BOOK - PUNEET DOGRACHAPTER - APPLICATION OF DERIVATIVESEXERCISE - PREV YEAR QUESTIONS85videos
APPLICATION OF DERIVATIVES
- BOOK - PUNEET DOGRACHAPTER - 3-D GEOMETRYEXERCISE - PREV YEAR QUESTIONS108videos
3-D GEOMETRY
- BOOK - PUNEET DOGRACHAPTER - AREA BOUNDED BY CURVESEXERCISE - PREV YEAR QUESTIONS39videos
AREA BOUNDED BY CURVES
Similar Questions
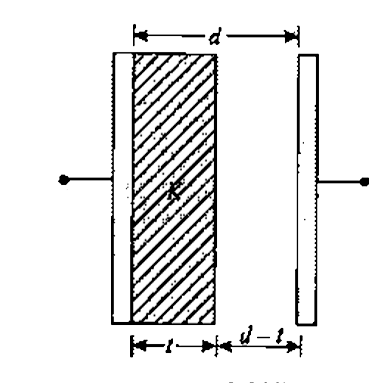
A parallel plate capacitor consists of two metal plates of area A and separation d. A slab of thickness t and electric constant K is inserted between the plates with its faces parallel to the plates and having the same surface area as that of the plates. Find the capacitance of the system.
IF K=2, for what value of t/d will the capacitance of the system be 3/2 times that of the air capacitor? Calculate the energy in the two cases and account for the energy change.
 View Solution
View SolutionAn open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket, where we do not take into account the handle of the bucket. Also, find the volume of water the bucket can hold.
View Solution
Knowledge Check
- Question 1 - Select One
A cylindrical jar without a lid has to be constructed using a given surface area of a metal sheet if the capacity of the jar times the height of the jar The value of k is
A1B2C3D4 - Question 2 - Select One
A conical vessel is to be prepared out of a circular sheet of metal of unit radius in order that the vessel has maximum value, the sectorial area that must be removed from the sheet is A1 and the area of the given sheet is A2, then A2A1 is equal to
A3+√6B7+√5C2+√5D3+√2 - Question 3 - Select One
X-ray are produced in coolidge tube. It consists of a thick glass bulb evacuated about 10−0 cm of Hg so that no discharge can pass in it. A cathode serves as source of electron is made up of tungsten filament heated by a low voltage current. A cylindrical metal shield S surrounds the filament and is kept at negative potential with respect to the filament is focuses the electron emitted from the filament on the target T. the target is mounted on the surface of a copper block fixed to the end of a copper rod . The rod is fitted with fins with for air cooling or cooled by circulating water A potential difference of about 20.000 V is applied across the tube to acceleration the electrons. The acceleration electrons strike to the target and produces continous and characteristic x-rays.
In the coolidge tube experiment platinum is used as target material for the emission of k-series x-rays. The K,L and M energy level of this element are 7.8×104eV,1.2×104eVand3×103eV respectively C=3×108m/s,1eV=1.6×10−19andh=6.23×10−34 j-s. The wavelength of kα lines will beA0.188 ÅB0.376 ÅC0.999 ÅD0.25 Å
A parallel plate capacitor is to be constructed which can store q=10μC charge at V=1000 volt. The minimum plate area of the capacitor is required to be A1 when space between the plates has air. If a dielectric of constant K=3 is used between the plates, the minimum plate area required to make such a capacitor is A2. The breakdown field for the dielectric is 8 times that of air. Find A1A2
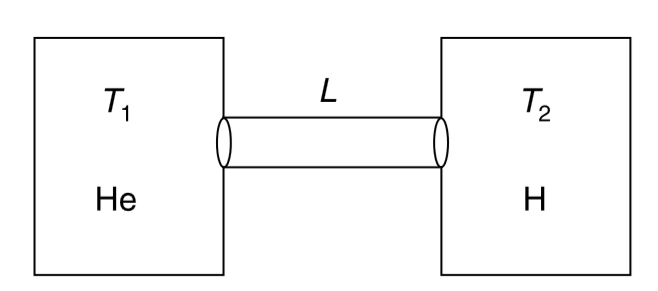
View SolutionTwo identical adiabatic containers of negligible heat capacity are connected by conducting rod of length L and cross sectional area A. Thermal conductivity of the rod is k and its curved cylindrical surface is well insulated from the surrounding. Heat capacity of the rod is also negligible. One container is filled with n moles of helium at temperature T1 and the other one is filled with equal number of moles of hydrogen at temperature T2(<T1). Calculate the time after which the temperature difference between two gases will becomes half the initial difference.
 View Solution
View SolutionIn a toys manufacturing company, wooden parts are assembled and painted to prepare a toy. One specific toy is in the shape of a cone mounted on a cylinder.
For the wood processing activity center, the wood is taken out of storage to be sawed, after which it undergoes rough polishing, then is cut, drilled and has holes punched in it. It is then fine polished using sandpaper.

For the retail packaging and delivery activity center, the polished wood sub-parts are assembled together, then decorated using paint.
The total height of the toy is 26 cm and the height of its conical part is 6 cm. The diameters of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm.
If its cylindrical part is to be painted yellow, the surface area need to be painted isView SolutionIn a toys manufacturing company, wooden parts are assembled and painted to prepare a toy. One specific toy is in the shape of a cone mounted on a cylinder.
For the wood processing activity center, the wood is taken out of storage to be sawed, after which it undergoes rough polishing, then is cut, drilled and has holes punched in it. It is then fine polished using sandpaper.

For the retail packaging and delivery activity center, the polished wood sub-parts are assembled together, then decorated using paint.
The total height of the toy is 26 cm and the height of its conical part is 6 cm. The diameters of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm.
If its conical part is to be painted green, the surface area need to be painted isView SolutionThe diameter of a cylindrical jar is increased by 25% . By what percent must the height of the jar be decreased so that there is no change is its volume ?
View Solution
