Two wires of equal dimensions and young's modulus Y1 and Y2 are connected end to end. What is the equivalent young's modulus for the combination?
Y1+Y22
√Y1+Y2
2Y1Y2Y1+Y2
√Y21y222
The correct Answer is:C
To find the equivalent Young's modulus Y for two wires of equal dimensions and Young's moduli Y1 and Y2 connected end to end, we can follow these steps:
1. Understand the Setup:
- We have two wires, both with length L and cross-sectional area A.
- The Young's moduli of the wires are Y1 and Y2.
- When connected end to end, the total length of the combination becomes L+L=2L.
2. Define Young's Modulus:
- Young's modulus Y is defined as the ratio of stress to strain:
Y=StressStrain=F/AΔL/L
- Here, F is the force applied, A is the cross-sectional area, ΔL is the change in length, and L is the original length.
3. Calculate Change in Length for Each Wire:
- For the first wire with Young's modulus Y1:
ΔL1=FLAY1
- For the second wire with Young's modulus Y2:
ΔL2=FLAY2
4. Total Change in Length:
- Since the wires are connected in series, the total change in length ΔL is the sum of the changes in length of both wires:
ΔL=ΔL1+ΔL2=FLAY1+FLAY2
5. Combine the Expressions:
- Factor out common terms:
ΔL=FLA(1Y1+1Y2)
6. Express the Equivalent Young's Modulus:
- The equivalent Young's modulus Y for the combined wire of length 2L is given by:
Y=F/AΔL/(2L)
- Substituting the expression for ΔL:
Y=F/AFLA(1Y1+1Y2)/(2L)
- Simplifying this gives:
Y=2LL⋅11Y1+1Y2=2Y1Y2Y1+Y2
Final Result:
The equivalent Young's modulus Y for the combination of the two wires is:
Y=2Y1Y2Y1+Y2
- We have two wires, both with length L and cross-sectional area A.
- The Young's moduli of the wires are Y1 and Y2.
- When connected end to end, the total length of the combination becomes L+L=2L.
- Young's modulus Y is defined as the ratio of stress to strain:
Y=StressStrain=F/AΔL/L
- Here, F is the force applied, A is the cross-sectional area, ΔL is the change in length, and L is the original length.
- For the first wire with Young's modulus Y1:
ΔL1=FLAY1
- For the second wire with Young's modulus Y2:
ΔL2=FLAY2
- Since the wires are connected in series, the total change in length ΔL is the sum of the changes in length of both wires:
ΔL=ΔL1+ΔL2=FLAY1+FLAY2
- Factor out common terms:
ΔL=FLA(1Y1+1Y2)
- The equivalent Young's modulus Y for the combined wire of length 2L is given by:
Y=F/AΔL/(2L)
- Substituting the expression for ΔL:
Y=F/AFLA(1Y1+1Y2)/(2L)
- Simplifying this gives:
Y=2LL⋅11Y1+1Y2=2Y1Y2Y1+Y2
The equivalent Young's modulus Y for the combination of the two wires is:
Y=2Y1Y2Y1+Y2
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
A horizontal rod suspended from two wires of same length and cross - section. Their Young's modulus are Y1 and Y2 respectively. The equivalent Young's modulus will be

View SolutionTwo wires of equal length and cross sectional area suspended as shown in
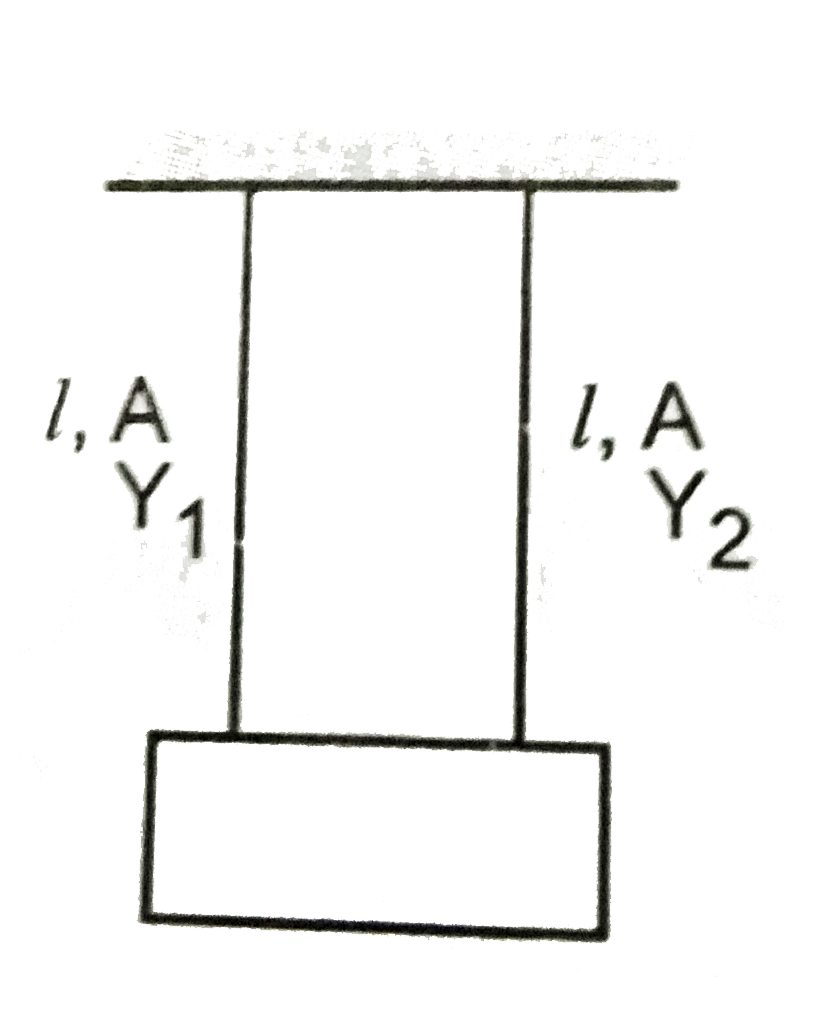
Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
View Solution
Knowledge Check
Young's modulus of a wire depends on
Adiameter of the wireBmass hanging from the wireClength of the wireDÂ material of the wireIf stress is numbercially equal to young's modulus, the elongation will be
A1/4 the original lengthB1/2 the orginla lengthCequal to the orginal lengthDtwice the original lengthWhat are dimensions of Young's modulus of elasticity?
A[ML−1T−2]B[MLT−2]C[MLT−1]Dnone of these
A wire of length L and area of cross section A is made of a material of Young's modulus Y. If it is stretched by an amount x, the work done is given by
View SolutionTo determine Young's modulus of the material of a wire,
View SolutionIf the length of a wire is doubled, then its Young's modulus
View SolutionTwo wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y1 andY2 respectively. The equivalent Young's modulil will bebr>
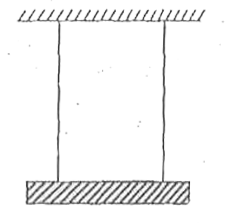
View SolutionTwo wires of equal length and cross-section area suspended as shown in figure. Their Young's modulus are Y1 and Y2 respectively. The equavalent Young's modulus will be

View Solution
