Find the magnitude of induced filed " En " at a point r (>R) where a uniform but time varying magnetic field (dBdt=b) exists in a region of radius R .
To find the magnitude of the induced electric field En at a point r (where r>R) due to a uniform but time-varying magnetic field, we can follow these steps:
1. Understand the Problem:
We have a uniform magnetic field that is changing with time, represented as dBdt=b. This magnetic field exists in a circular region of radius R. We need to find the induced electric field at a point outside this region, specifically at a distance r where r>R.
2. Use Faraday's Law of Electromagnetic Induction:
According to Faraday's law, the induced electromotive force (emf) E around a closed loop is equal to the negative rate of change of magnetic flux through that loop:
E=−dΦBdt
where ΦB is the magnetic flux.
3. Calculate the Magnetic Flux:
The magnetic flux ΦB through the circular area of radius R is given by:
ΦB=B⋅A=B⋅πR2
where A is the area of the circle, A=πR2.
4. Differentiate the Magnetic Flux:
Since B is changing with time, we differentiate the magnetic flux:
dΦBdt=ddt(B⋅πR2)=πR2dBdt
Substituting dBdt=b, we have:
dΦBdt=πR2b
5. Relate Induced emf to Induced Electric Field:
The induced emf E around a circular path of radius r is also given by:
E=En⋅2πr
where En is the magnitude of the induced electric field.
6. Set the Two Expressions for emf Equal:
From Faraday's law, we have:
En⋅2πr=πR2b
7. Solve for the Induced Electric Field En:
Rearranging the equation gives:
En=πR2b2πr=R2b2r
Final Result:
Thus, the magnitude of the induced electric field En at a point r (where r>R) is:
En=R2b2r
We have a uniform magnetic field that is changing with time, represented as dBdt=b. This magnetic field exists in a circular region of radius R. We need to find the induced electric field at a point outside this region, specifically at a distance r where r>R.
According to Faraday's law, the induced electromotive force (emf) E around a closed loop is equal to the negative rate of change of magnetic flux through that loop:
E=−dΦBdt
where ΦB is the magnetic flux.
The magnetic flux ΦB through the circular area of radius R is given by:
ΦB=B⋅A=B⋅πR2
where A is the area of the circle, A=πR2.
Since B is changing with time, we differentiate the magnetic flux:
dΦBdt=ddt(B⋅πR2)=πR2dBdt
Substituting dBdt=b, we have:
dΦBdt=πR2b
The induced emf E around a circular path of radius r is also given by:
E=En⋅2πr
where En is the magnitude of the induced electric field.
From Faraday's law, we have:
En⋅2πr=πR2b
Rearranging the equation gives:
En=πR2b2πr=R2b2r
Thus, the magnitude of the induced electric field En at a point r (where r>R) is:
En=R2b2r
Similar Questions
(A): In equation F=q(E+v×B) when v = 0, any force on the charge must arise from the electric field term E alone
(R): To explain, the existence of induced emf or induced current in static conductor kept in time - varying magnetic field, we must assume that a time - varying magnetic field generates an electric field
View SolutionA circular wire loop of radius R is placed in the X-Y plane with its centre at the origin. The loop carries a current I in the clockwise direction when viewed from a point on the positive Z-axis. A uniform magnetic field →B=B0(ˆi+√3ˆj2) exists in the region x>R√32. The magnitued of the magnetic force on the loop due to the magnetic field is B0IRn. The value of n is______________.
View SolutionA reacangular loop if size (2m×1m) is placed in x-y plane. A uniform but time varying magnetic field of strength T where t is the time elsapsed in second exists in sosace. The magnitude of induced emf (in V) at time t is
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA: Faraday's law is an experimental law. R: Time varying magnetic field cannot generale induced emf.
View SolutionTime varying magnetic filed is present in a circular region of radius R. Match the proper entries from column-2 to column-1 using the codes given below the columns,
Column IColumn II(P) An unsteady magnetic field(1) Electric field is perpendicular to the length of rod (Q)Induced electric field at a point within magnetic field (r gtR)(2)r2dBdt(R)Induced electric field at a point out side the magnetic field (r lt R)(3)R22rdBdt(S)If a rod is placed along the diameter of the magnetic field(4) induced electric field
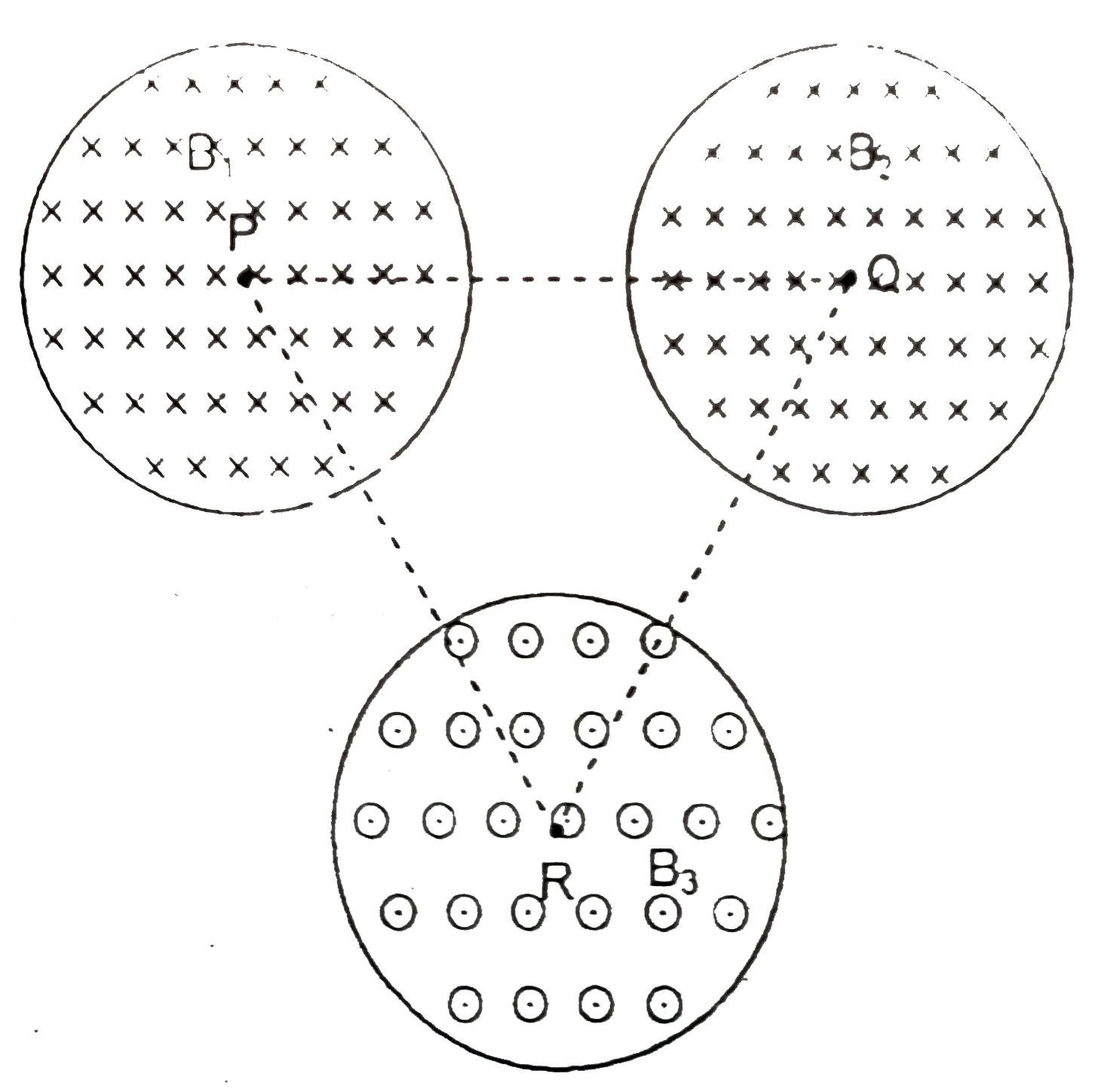
View SolutionIn the figure B1, B2 and B3 represent uniform time varying magnetic fields in three different infinitely long cylindrical regions with axis passing through P, Q and R and perpendicular to the plane of the paper. PQR is an equilateral triangle of side 4√3r, where r is radius of each cylindrical region (r=1m). The magnetic inductions vary with time t as B1=A+at, B2=A−bt and B3=A+ct. Here a=2Tesla/s, b=2Tesla/s and c=1Tesla/s and A is a constant with dimensions of magnetic field and 't' is time. Find the induced electric field strength at the centroid of the triangle PQR.
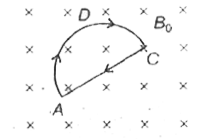
View SolutionFigure show a conducting loop ADCA carrying current I and placed in a region of uniform magnetic field B0. The part ADC forms a semicircle of radius R. The magnitude of force on the semicircle part of the loop is equal to
View SolutionMagnetic induction at a point due to a small element of current carrying conductor is
View SolutionA wire loop confined in a plane is rotated in its open plane with some angular velocity. A uniform magnetic field exists in the region. Find the emf induced in the loop.
View Solution
