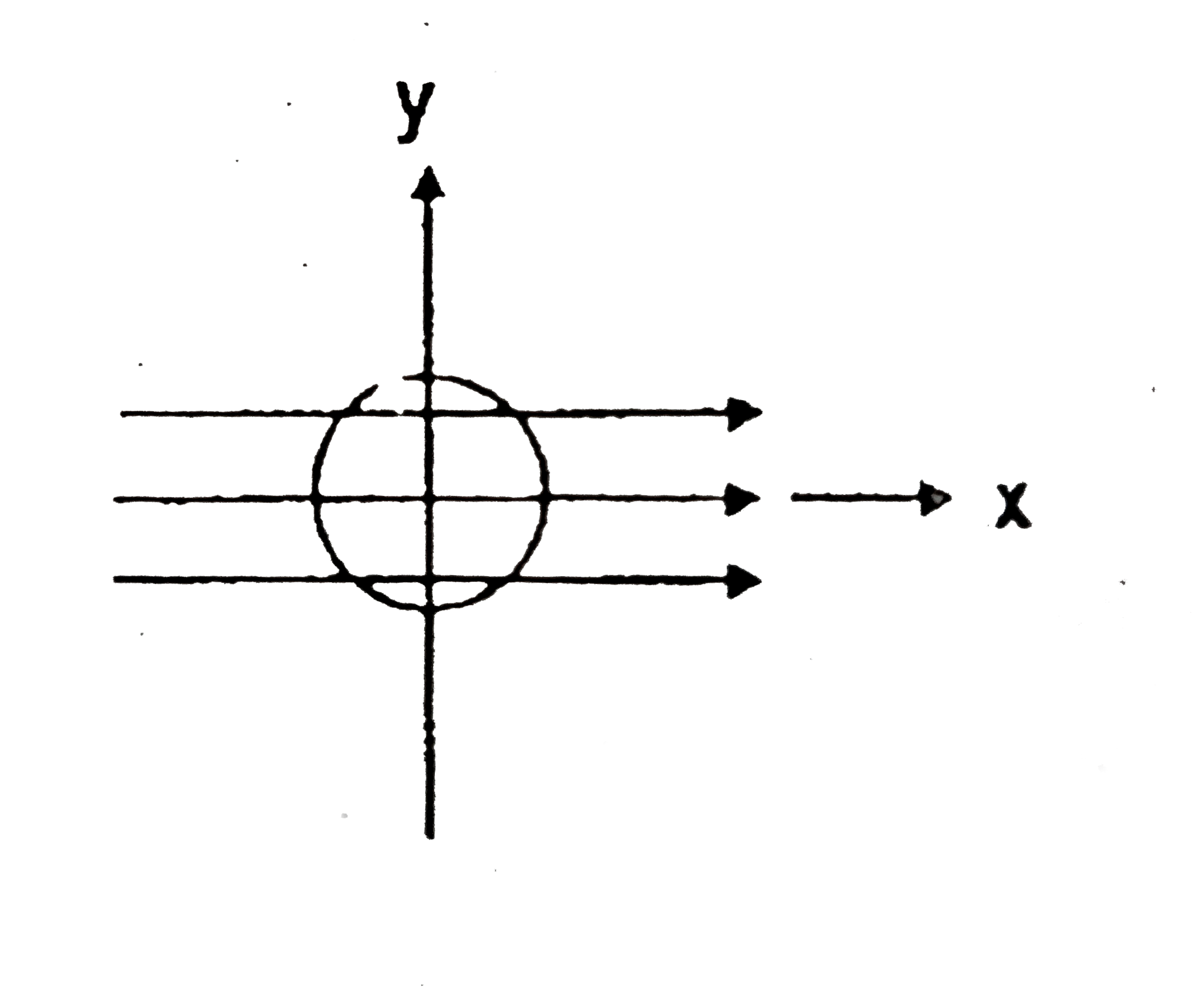
A conducting loop of resistance R and radius r has its center at the origin of the co-ordinate system in a magnetic field of induction B. When it is rotated about Y-axis through 90∘, net charge flown in the coil is directly proportional to
B
R
r2
r
The correct Answer is:A, C
emf is induced when the flux ϕ varies, the variation flux dϕ during time dt is given as
E = dϕdt
⇒∫ϕ2ϕ1dϕ=Δϕ=∫ Edt … (1)
⇒ The total charge flown in the loop = q = ∫ i dt
q = ∫ER dt ... (2)
using (1) and (2)
q = ΔϕR
Where Δϕ = change in flux given as Δϕ=ϕ2−ϕ1= B. (πr2) because intially to flux is linked with the coil and it has maximum flux linkage ϕ2 = B πr2when turned through 90∘ , the flux is reduced to zero .
⇒q=πBr2R
⇒ i.e. q ∝ B
q ∝r2
q ∝ (1/ R)
Hence (A) & (c ) are correct .
Similar Questions
A loop is kept so that its center lies at the origin of the coordinate system. A magnetic field has the induction B pointing along Z axis as shown in the figure

View SolutionA conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA sphere of radius R has a uniform distribution of electric charge in its volume. At a distance x from its centre, for x<R, the electric field is directly proportional to
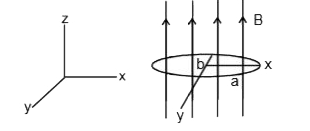
View SolutionAn elliptical loop having resistance R, of semi major axis a, and semi minor axis b is placed in a magnetic field as shown in the figure. If the loop is rotated about the x-axis with angular frequency ω, the average power loss in the loop due to Joule heating is :
View SolutionSpace is divided by the line AD into two regions. Region I is field free and the Region II has a unifrom magnetic field B direction into the plane of the paper. ACD is a simicircular conducting loop of radius r with center at O, hte plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity ω about an axis passing through O and the perpendicular to the plane of the paper. The effective resistance of the loop is R.
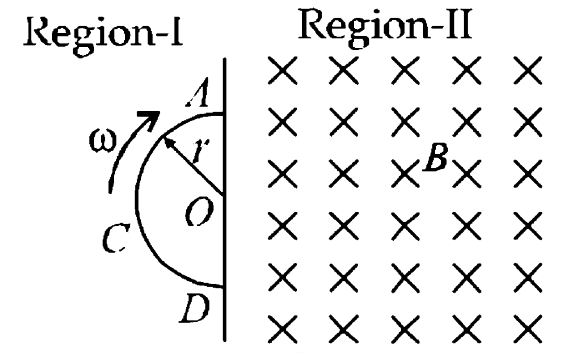
(i) obtain an expression for hte magnitude of the induced cureent in the loop.
(ii) Show the direction of the current when the loop is entering into the Rigion II.
Plot a graph between the induced e.m.f and the time of roation for two periods or rotation.
View SolutionSpace is divided by the line AD into two regions. Region I is field free and the Region II has a unifrom magnetic field B direction into the plane of the paper. ACD is a simicircular conducting loop of radius r with center at O, hte plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity ω about an axis passing through O and the perpendicular to the plane of the paper. The effective resistance of the loop is R.

(i) obtain an expression for hte magnitude of the induced cureent in the loop.
(ii) Show the direction of the current when the loop is entering into the Rigion II.
Plot a graph between the induced e.m.f and the time of roation for two periods or rotation.
View SolutionA coil of 40Ω resistance has 100 turns and radius 6mm us connected to ammeter of resistance of 160ohms. Coil is placed perpendicular to the magnetic field. When coil is taken out of the field, 32μC charge flows through it. The intensity of magnetic field will be
View SolutionA dc motor works on the principle that a current carrying coil, when placed in a magnetic field experiences a torque. The arrangement consists of a coil suspended in a region of magnetic field. When a current is passed through the coil, it experiences torque and starts rotating. A simple arrangement is shown below.
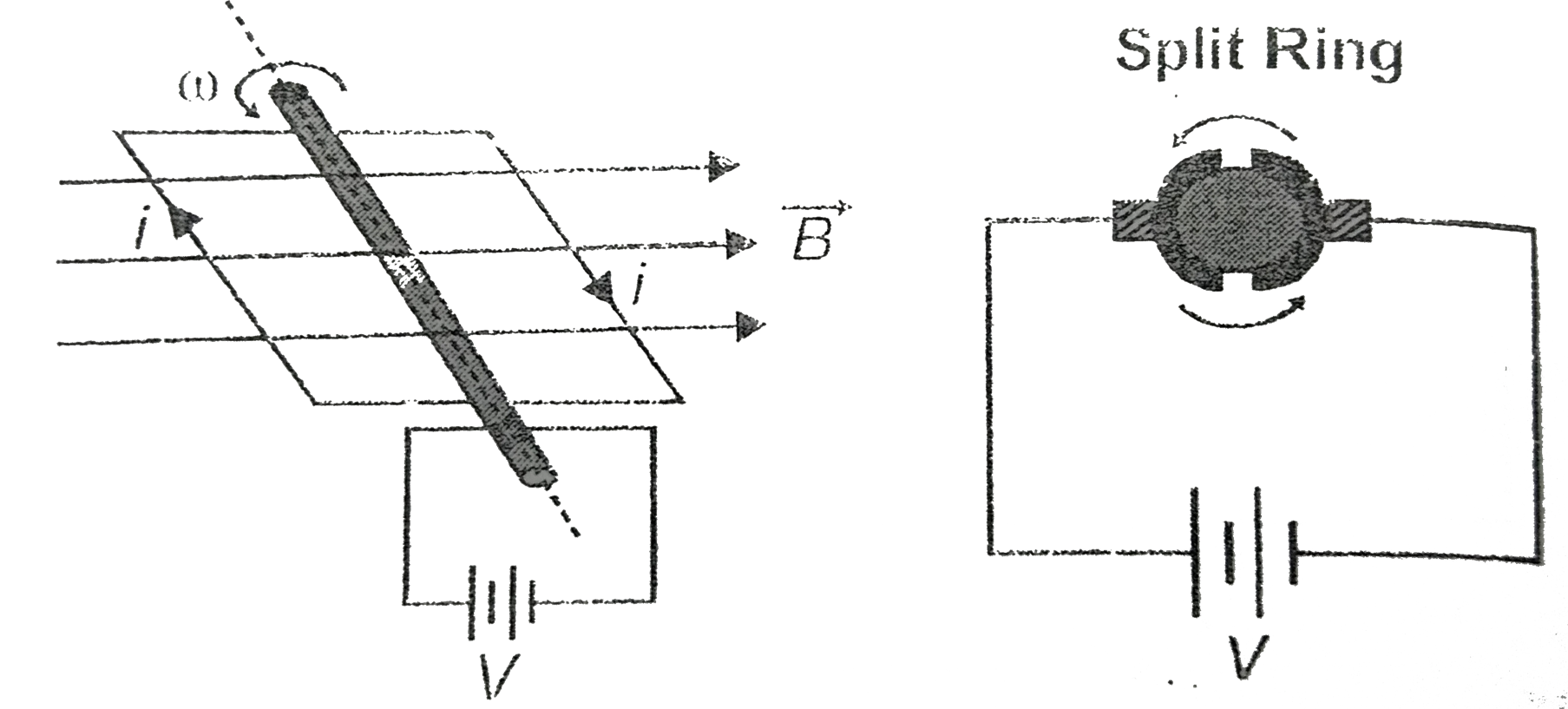
The coil rotates under the action of torque. The current is supplied to the coil by an arrangement of two sliding contacts and a split ring. As the coil rotates, the magnetic flux linked with the coil changes. This leads to production of an induced emf ε in the coil. By Lenz's law, the induced emf opposes the applied voltage and therefore, it is called back emf. If R is the resistance in the coil, the current i flowing through the coil at any instant is i=V−εR. The back emf is developed due to induction and it is directly proportional to speed of rotation and it is directly proportional to speed of rotation of the motor. There is a continuous power loss i2R in the motor, in form of heat.
When a dc motor is running unloaded (full speed) the current through it is 1 A. What will be the current flowing through the motor, when it is loaded to run at half its maximum speed, it applied voltage is 10 V and armature resistance is 5Ω
View Solution

