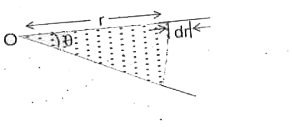
A metallic rod of mass m length R is pivoted at O. It is free to rotate about a horizontal axis passing through O . An inward magnetic field is applied as shown in the figure. Find the ratio of maximum electric field inside the metallic rod to the applied magnetic field induction .

The induced emf between O and P
ε=−dϕdt=−d(BA)dt=−BdAdt
ε=−Bddt[r22θ]=−Br2ω2(∵ω=dθdt)
The potential gradient dεdr=(−Br2ω2)ddr(r2)=−Bωr
⇒ The corresponding electric field E = Bωr
⇒Emax=Bω R where ω = maximum angular speed of the rod that is possible when it becomes vertical . Conservation of meachanical energy between horizontal and vertical yield ,
ΔPEgr+ΔKEr=0
−mgR2+12I0ω2=0
⇒ω=√3gRR
⇒EmaxB=√3gR
Similar Questions
Find the magnetic field at point O shown in the figure

View SolutionWhy a thick metal plate oscillating about a horizontal axis stops when a strong magnetic field is applied on the plane?
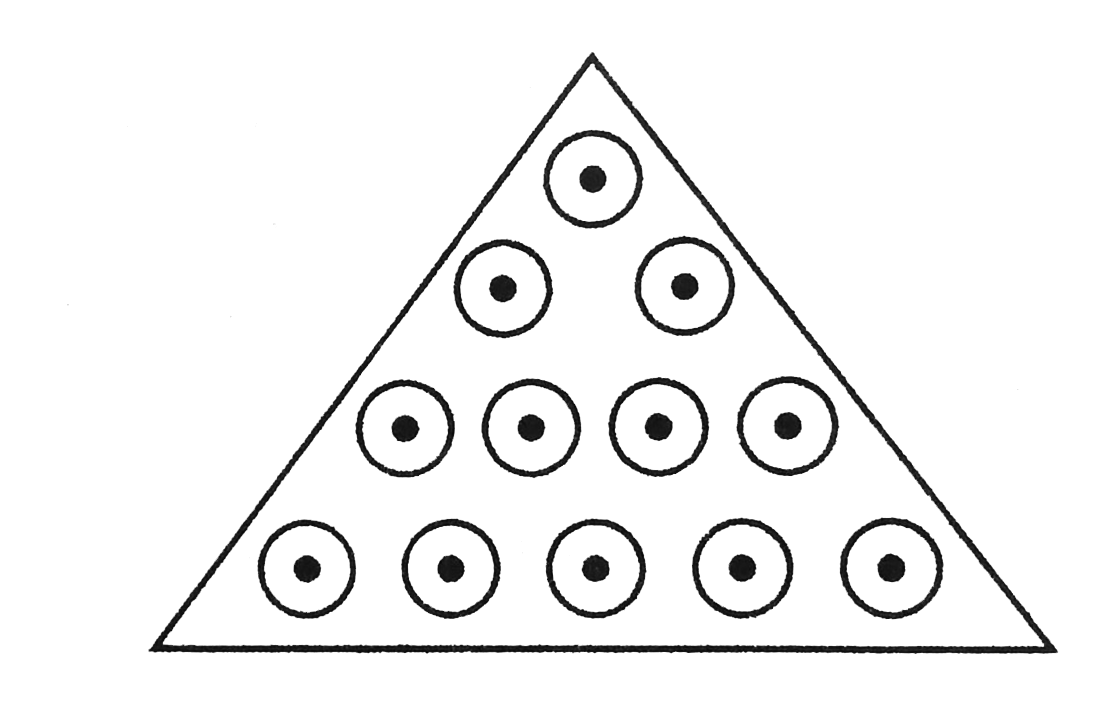
View SolutionA triangular loop is placed in a dot ⊙ magnetic field as shown in figure. Find the direction of induced current in the loop if magnetic field is increasing.
View SolutionFind the magnetic field at the centre O of the loop shown in the figure
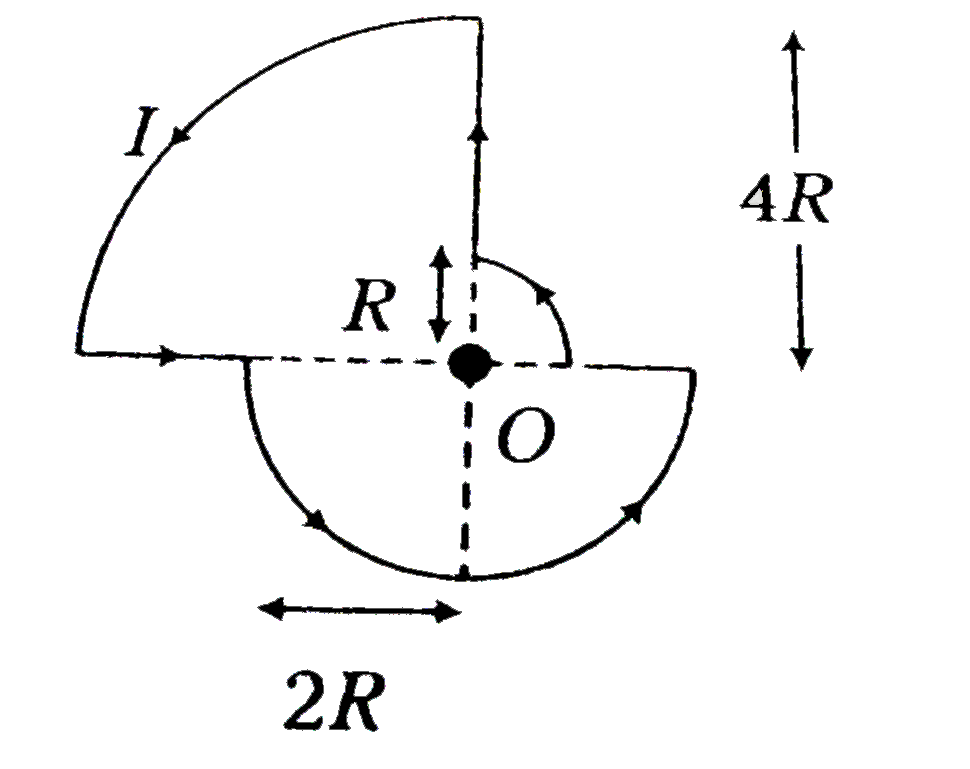
View SolutionFind the magnetic field at the centre O of the loop shown in the figure
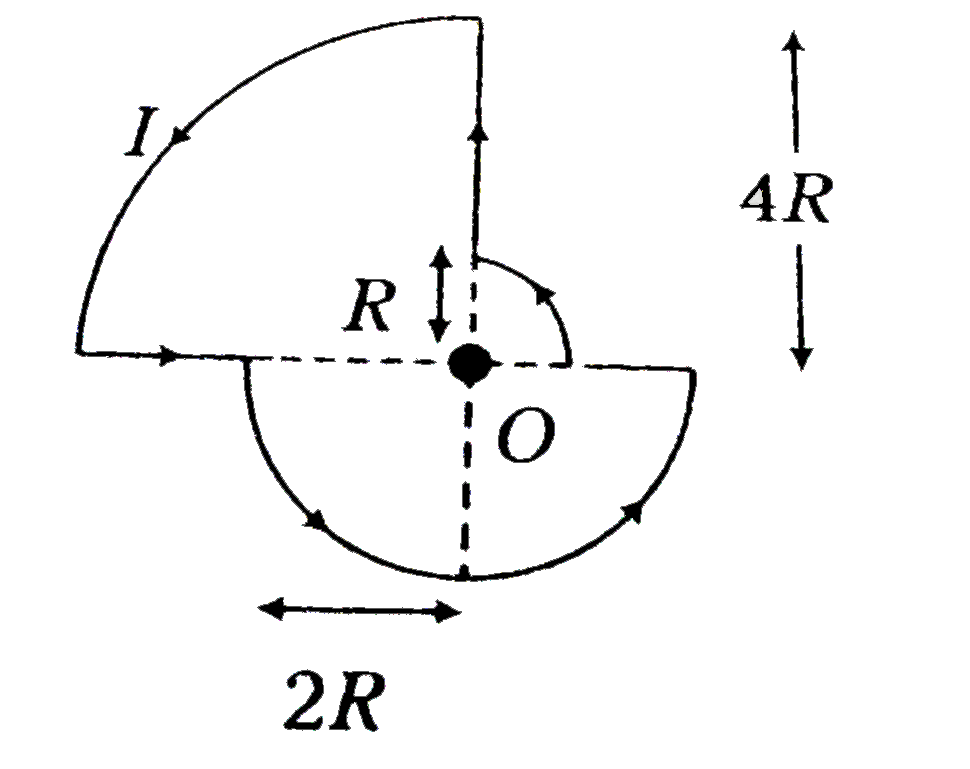
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionA uniform rod of length L is free to rotate about an axis passing through O. Inititally the rod is horizontal. The rod is relased from this position. Match column I with column II
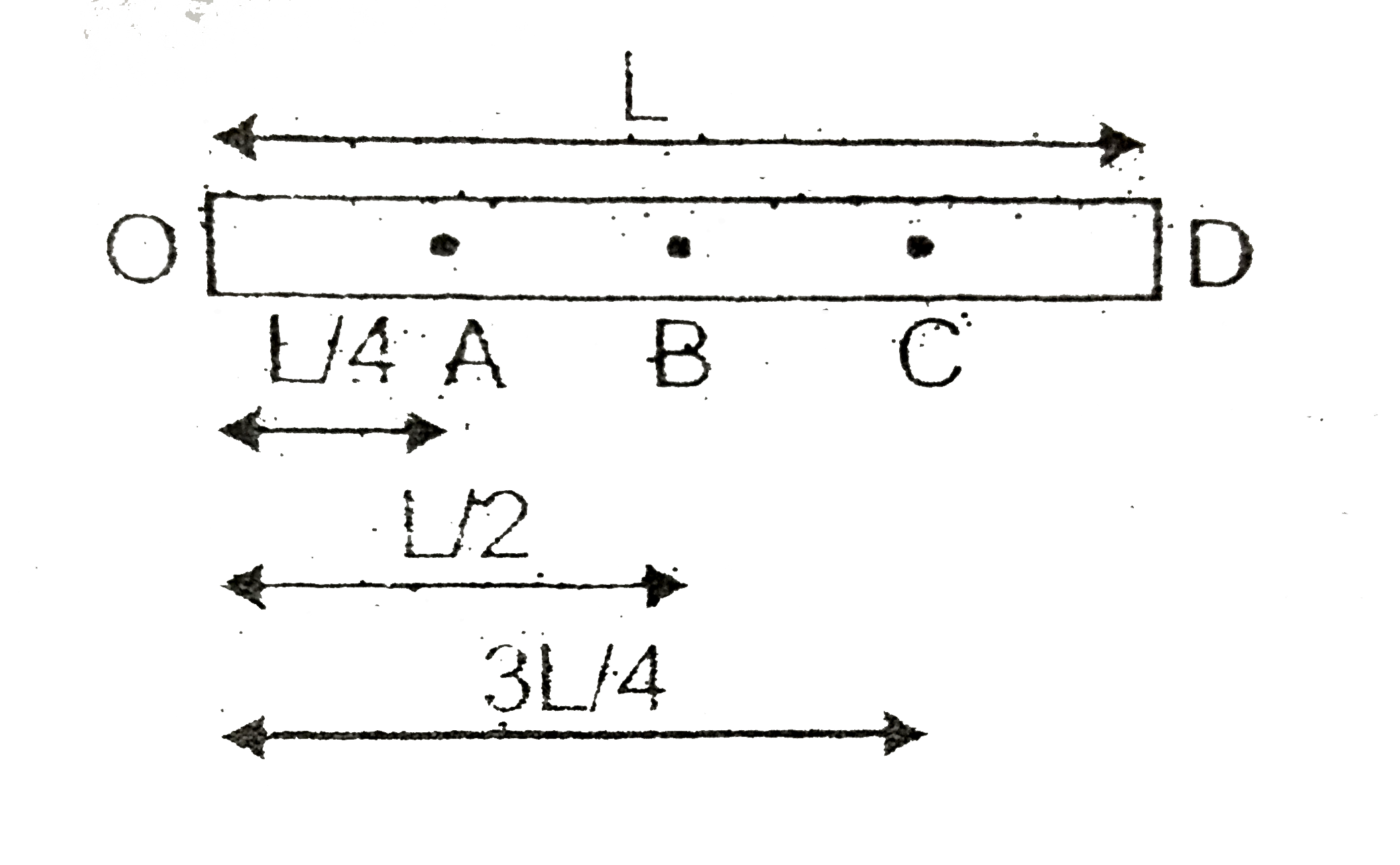
View Solution
A uniform rod of length 4l and mass m is free to rotate about a horizontal axis passing through a point distant l from its one end. When the rod is horizontal its angular velocity is ω as shown in figure. calculate
(a). reaction of axis at this instant,
(b). Acceleration of centre of mass of the rod at this instant.
(c). reaction of axis and acceleration of centre mass of the rod when rod becomes vertical for the first time.
(d). minimum value of ω, so that centre of rod can complete circular motion.
View SolutionA metallic rod of length l is rotated at a constant angular speed ω, normal to a uniform magnetic field B. Derive an expression for the current induced in the rod, if the resistance of the rod is R.
View SolutionA uniform rod AB of length l and mass m is free to rotate about an Axis passing through A and perpendicular to length of the rod. The rod is released from rest as shown in figure. Given that the moment of inertia of the rod about A is ml23 The initial angular acceleration of the rod will be
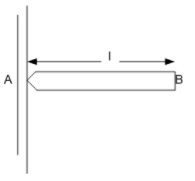
View Solution
