A massive platform of mass M is moving with speed v=6ms−1 At t = 0, at body of mass m(m<<M) is gently placed on the platform. If c-efficient of friction between the body and platform is μ=0.3andg=10m/s2, then
the body covers a distance of 3 m on the platform in the direction of motion of the platform.
the body covers a distance of 3 m on the platform opposite to the direction of motion of the platform before coming to rest.
the body covers a distance of 6 m on the platform in the direction of motion of the platform.
the body covers a distance of 6 m on the platform opposite to the direction of motion of the platform before coming to rest.
The correct Answer is:D
To solve the problem step by step, we need to analyze the situation involving the platform and the body placed on it.
Step 1: Understand the Initial Conditions
- The platform is moving with a speed v=6m/s.
- A body of mass m (where m≪M) is placed on the platform at t=0.
- The coefficient of friction between the body and the platform is μ=0.3.
- The acceleration due to gravity is g=10m/s2.
Step 2: Determine the Initial Velocity of the Body
When the body is placed on the moving platform, it initially has no velocity relative to the platform. However, since the platform is moving, the body will have an initial velocity of:
vbody=−v=−6m/s
This negative sign indicates that the body is moving in the opposite direction to the platform's motion.
Step 3: Calculate the Frictional Force
The frictional force acting on the body can be calculated using:
Ffriction=μ⋅m⋅g
Substituting the values:
Ffriction=0.3⋅m⋅10=3mN
Step 4: Determine the Acceleration of the Body
Using Newton's second law, the acceleration a of the body due to friction is:
F=m⋅a⟹3m=m⋅a⟹a=3m/s2
This acceleration is directed opposite to the motion of the platform.
Step 5: Use Kinematic Equation to Find Distance
We can use the kinematic equation:
v2=u2+2as
Where:
- v=0 (final velocity when the body comes to rest),
- u=−6m/s (initial velocity),
- a=−3m/s2 (acceleration, negative because it opposes the motion),
- s is the distance covered by the body.
Substituting the values into the equation:
0=(−6)2+2(−3)s
0=36−6s
6s=36⟹s=6m
Conclusion
The body covers a distance of 6m on the platform in the direction opposite to the motion of the platform before coming to rest.
Final Answer
The distance covered by the body before coming to rest is 6m in the direction opposite to the motion of the platform.
---
- The platform is moving with a speed v=6m/s.
- A body of mass m (where m≪M) is placed on the platform at t=0.
- The coefficient of friction between the body and the platform is μ=0.3.
- The acceleration due to gravity is g=10m/s2.
When the body is placed on the moving platform, it initially has no velocity relative to the platform. However, since the platform is moving, the body will have an initial velocity of:
vbody=−v=−6m/s
This negative sign indicates that the body is moving in the opposite direction to the platform's motion.
The frictional force acting on the body can be calculated using:
Ffriction=μ⋅m⋅g
Substituting the values:
Ffriction=0.3⋅m⋅10=3mN
Using Newton's second law, the acceleration a of the body due to friction is:
F=m⋅a⟹3m=m⋅a⟹a=3m/s2
This acceleration is directed opposite to the motion of the platform.
We can use the kinematic equation:
v2=u2+2as
Where:
- v=0 (final velocity when the body comes to rest),
- u=−6m/s (initial velocity),
- a=−3m/s2 (acceleration, negative because it opposes the motion),
- s is the distance covered by the body.
0=(−6)2+2(−3)s
0=36−6s
6s=36⟹s=6m
The body covers a distance of 6m on the platform in the direction opposite to the motion of the platform before coming to rest.
The distance covered by the body before coming to rest is 6m in the direction opposite to the motion of the platform.
Similar Questions
A body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
View SolutionA body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
View Solution
In the given figure, a long platform of mass m is placed on frictionless surface. Two blocks of masses 4 m and m (where m=10 kg) are placed on the platform. For both blocks, the coefficient of static friction with platform equal to 0.16 and the coefficient of kinetic friction equal to 0.10 the blocks are connected by a light ideal string through a light pulley (mounted at a movable massless stand). Which is acted upon by an unknown horizontal force F. if the acceleration of the platform is 2m/s2. Find the value of unknown force F and acceleration of blocks 4 m and m on a1 and a2 respectively.
View SolutionA rod AB of length 2m is hinging at point A and its other end B is atteched to a platform on which a point of mass m is kept. Rod rotates about point A maintaing angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path.If the coeffiicent of staic friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the plateform (g=10ms−2)
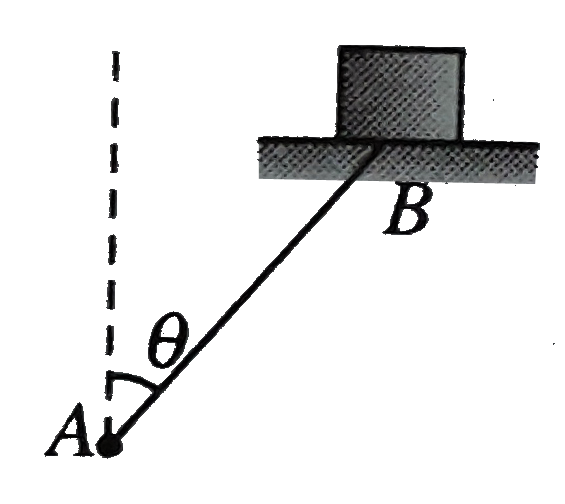
View SolutionA rod AB of length 2m is hinging at point A and its other end B is atteched to a platform on which a point of mass m is kept. Rod rotates about point A maintaing angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path.If the coeffiicent of staic friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the plateform (g=10ms−2)

View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)

View SolutionA boy is sitting on the horizontal platform of a joy wheel at a distance of 5 m from the center. The wheel begins to rotate and when angular speed exceeds 1 rad/s, the boy just slips. The coefficient of friction between the boy and the wheel is (g=10m/s2)
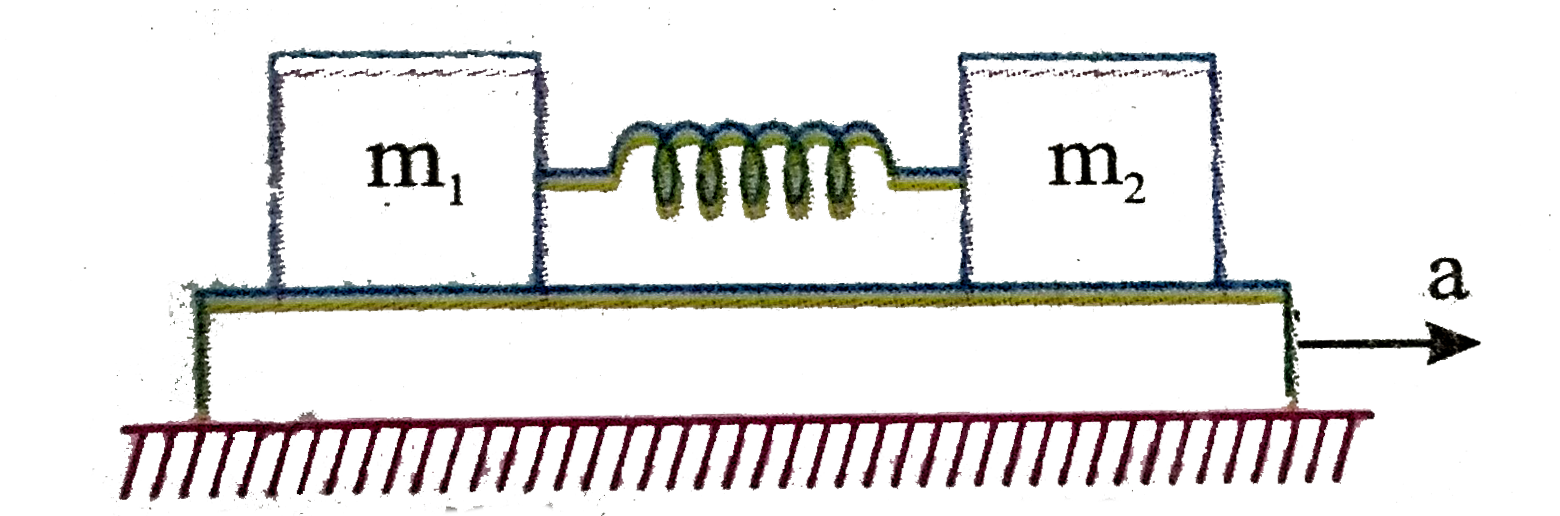
View SolutionTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
View SolutionTwo particles of mass M=3kg each are kept on a horizontal circular platform on two mutually perpendicular radii at equal distance R=1m from the centre of the table. The particles are connected with a string,which is just taught when the platform is not rotating.Coefficient of friction between the platform and block is μ=0.4.Then the maximum angular speed (ω in radsec) of platform about its centre so that the blocks remain stationary relative to platform is (take g=10.ms2 )
View SolutionA block of mass m is gently placed over a massive plank moving horizontal over a smooth surface with velocity 10ms−1. The coefficient of friction between the block and the plank is 0.2. The distance travelled by the block till it slides on the plank is [g=10ms−2]
View Solution
