Centre of mass is at point X (1,1,1) when system consists of particles of masses 2, 3, 4 and 5 kg. If the centre of mass shifts to point Y (2, 2, 2) on removal of the mass of 5 kg. What was its position ?
To find the position of the 5 kg mass when the center of mass shifts from point X (1, 1, 1) to point Y (2, 2, 2) upon its removal, we can follow these steps:
Step 1: Understand the Center of Mass Formula
The center of mass (CM) of a system of particles is given by the formula:
CM=m1→r1+m2→r2+m3→r3+…m1+m2+m3+…
where mi is the mass of each particle and →ri is the position vector of each particle.
Step 2: Set Up the Initial Conditions
Initially, we have three masses (2 kg, 3 kg, and 4 kg) and the center of mass is at point X (1, 1, 1). Let’s denote the positions of the 2 kg, 3 kg, and 4 kg masses as →r1,→r2,→r3 respectively.
Step 3: Calculate the Total Mass
The total mass of the system before the removal of the 5 kg mass is:
Minitial=2+3+4+5=14 kg
Step 4: Calculate the Center of Mass Before Removal
Using the center of mass formula:
(1,1,1)=2→r1+3→r2+4→r3+5→r514
where →r5 is the position of the 5 kg mass.
Step 5: Set Up the New Conditions After Removal
After removing the 5 kg mass, the center of mass shifts to point Y (2, 2, 2). The new total mass is:
Mnew=2+3+4=9 kg
The new center of mass can be expressed as:
(2,2,2)=2→r1+3→r2+4→r39
Step 6: Solve for the Position of the 5 kg Mass
From the equations, we can set up the following system:
1. 2→r1+3→r2+4→r3+5→r5=14(1,1,1)
2. 2→r1+3→r2+4→r3=9(2,2,2)
Subtracting these equations gives:
5→r5=14(1,1,1)−9(2,2,2)
Calculating the right-hand side:
5→r5=(14−18,14−18,14−18)=(−4,−4,−4)
Thus,
→r5=(−45,−45,−45)=(−0.8,−0.8,−0.8)
Final Answer
The position of the 5 kg mass is at (−0.8,−0.8,−0.8).
---
The center of mass (CM) of a system of particles is given by the formula:
CM=m1→r1+m2→r2+m3→r3+…m1+m2+m3+…
where mi is the mass of each particle and →ri is the position vector of each particle.
Initially, we have three masses (2 kg, 3 kg, and 4 kg) and the center of mass is at point X (1, 1, 1). Let’s denote the positions of the 2 kg, 3 kg, and 4 kg masses as →r1,→r2,→r3 respectively.
The total mass of the system before the removal of the 5 kg mass is:
Minitial=2+3+4+5=14 kg
Using the center of mass formula:
(1,1,1)=2→r1+3→r2+4→r3+5→r514
where →r5 is the position of the 5 kg mass.
After removing the 5 kg mass, the center of mass shifts to point Y (2, 2, 2). The new total mass is:
Mnew=2+3+4=9 kg
The new center of mass can be expressed as:
(2,2,2)=2→r1+3→r2+4→r39
From the equations, we can set up the following system:
1. 2→r1+3→r2+4→r3+5→r5=14(1,1,1)
2. 2→r1+3→r2+4→r3=9(2,2,2)
5→r5=14(1,1,1)−9(2,2,2)
Calculating the right-hand side:
5→r5=(14−18,14−18,14−18)=(−4,−4,−4)
Thus,
→r5=(−45,−45,−45)=(−0.8,−0.8,−0.8)
The position of the 5 kg mass is at (−0.8,−0.8,−0.8).
Similar Questions
Knowledge Check
Centre of mass of three particles of masses 1kg,2kgand3kg lies at the point (1,2,3) and centre of mass of another system of particles 3kgand2kg lies at the point (−1,3,−2). Where should we put a particle of mass 5kg so that the centre of mass of entire system lies at the centre of mass of first system ?
A(0, 0, 0)B(1, 3, 2)C(-1, 2, 3)D(3, 1, 8)
Three masses 3, 4 and 5 kg are placed at the centre of an equiliteral triangle of 1 m sides. Locate its centre of mass.
View SolutionMass centers of a system of three particles of masses 1,2,3kg is at the point (1m,2m,3m) and mass center of another group of two partices of masses 2kg and 3kg is at point (−1m,3m,−2m). Where a 5kg particle should be placed, so that mass center of the system of all these six particles shifts to mass center of the first system?
View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :
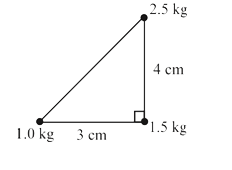
View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :

View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionCalculate the position of centre of mass of a system consisting of two particles of masses m_1 and m_2 separated by a distance L apar, from m_1?
View Solution