A standing wave given by the equation y=2Asin(πxL)sinωt is formed between the points x=- L and x = L The separation between two such particles, which have their maximum velocity half the maximum velocity of the antinodes and which are closest to the particle present f x=0, is L/k thon find the value of k.
To solve the problem, we will follow these steps:
Step 1: Understand the standing wave equation
The standing wave is given by the equation:
y=2Asin(πxL)sin(ωt)
This equation describes the displacement of the wave at any point x and time t.
Step 2: Determine the maximum velocity of the antinode
The maximum velocity of a particle in a standing wave can be found by differentiating the displacement with respect to time. The velocity v is given by:
v=∂y∂t=2Asin(πxL)ω
At the antinode (where sin(πxL)=1), the maximum velocity vmax is:
vmax=2Aω
Step 3: Find the condition for half the maximum velocity
We are looking for the points where the velocity is half of the maximum velocity of the antinode:
v=12vmax=12(2Aω)=Aω
Step 4: Set up the equation for velocity
From the velocity equation, we set:
2Asin(πxL)ω=Aω
Dividing both sides by Aω (assuming A and ω are not zero), we get:
2sin(πxL)=1
Step 5: Solve for x
Now, we simplify the equation:
sin(πxL)=12
The sine function equals 12 at:
πxL=π6andπxL=5π6
This gives us two solutions for x:
1. x=L6
2. x=5L6
Step 6: Find the separation between the two points
The separation between these two points is:
Δx=5L6−L6=4L6=2L3
Step 7: Relate the separation to L/k
According to the problem, this separation can be expressed as:
Δx=Lk
Setting the two expressions equal gives:
2L3=Lk
Step 8: Solve for k
To find k, we can cross-multiply:
2k=3
Thus,
k=32
Final Answer
The value of k is 3.
---
The standing wave is given by the equation:
y=2Asin(πxL)sin(ωt)
This equation describes the displacement of the wave at any point x and time t.
The maximum velocity of a particle in a standing wave can be found by differentiating the displacement with respect to time. The velocity v is given by:
v=∂y∂t=2Asin(πxL)ω
At the antinode (where sin(πxL)=1), the maximum velocity vmax is:
vmax=2Aω
We are looking for the points where the velocity is half of the maximum velocity of the antinode:
v=12vmax=12(2Aω)=Aω
From the velocity equation, we set:
2Asin(πxL)ω=Aω
Dividing both sides by Aω (assuming A and ω are not zero), we get:
2sin(πxL)=1
Now, we simplify the equation:
sin(πxL)=12
The sine function equals 12 at:
πxL=π6andπxL=5π6
This gives us two solutions for x:
1. x=L6
2. x=5L6
The separation between these two points is:
Δx=5L6−L6=4L6=2L3
According to the problem, this separation can be expressed as:
Δx=Lk
Setting the two expressions equal gives:
2L3=Lk
To find k, we can cross-multiply:
2k=3
Thus,
k=32
The value of k is 3.
Similar Questions
A stationary wave of amplitude A is generated between the two fixed ends x = 0 and x = L. The particle at x=L3 is a node. There are only two particle between x=L6andx=L3 which have maximum speed half of the maximum speed of the anti-node. Again there are only two particles between x= 0 and x=L6 which have maximum speed half of that at the antibodes. The slope of the wave function at x=L3 changes with respect to time according to the graph shown. The symbols μ,ωandA are having their usual meanings if used in calculations.
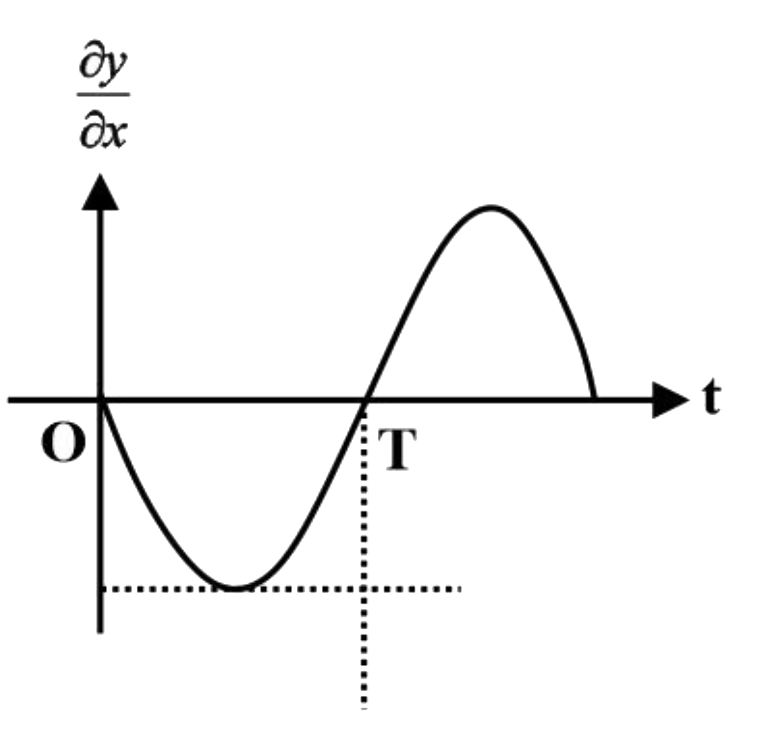
The time period of oscillations of a particle is
View SolutionThe equation of standing wave in a stretched string is given by {y=2sin[π2(x)]cos(20πt)} where x and y are in meter and t is in second. Then minimum separation between two particle which are at the antinodes and having same phase will be
View Solution
Knowledge Check
A transverse wave is represented by the equation
y=y0sin(2π)λ(vt−x)
For what value of λ is the particle velocity equal to two time the wave velocity ?Aλ=2πy0Bλ=2πy0/3Cλ=πy0/2Dλ=πy0
The displacement equation of a particle is x=3sin2t+4cos2t. The amplitude and maximum velocity will be respectively
View SolutionA particle is projected from the mid-point of the line joining two fixed particles each of mass m. If the separation between the fixed particles is l, the minimum velocity of projection of the particle so as to escape is equal to
View SolutionA travelling wave in a stretched string is described by the equation y=Asin(kx−ωt) the maximum particle velocity is
View SolutionA plane progressive wave is given by, y=0.30sin(40t−0.30x). Find the wavelength and the phase difference between two points at x=2 and x-7.232m. Also find the maximum particle velocity.
View SolutionTwo travelling waves of equal amplitudes and equal frequencies move in opposite direction along a string . They interfere to produce a standing wave having the equation .
y=Acoskxsinωt
in which A=1.0mm,k=1.57cm−1andω=78.5s−1. (a) Find the velocity and amplitude of the component travelling waves . (b) Find the node closest to the origin in the region x>0. ( c) Find the antinode closest to the origin in the region x>0 . (d) Find the amplitude of the particle at x=2.33cm.
View SolutionIf the equation sin2x−ksinx−3=0 has exactly two distinct real roots in [0,π], then find the values of k .
View SolutionThe equation of a travelling wave is,
Y=Asin2π(pt−x/5)
Then the ratio of maximum particle velocity to wave velocity is,
View Solution
