A stationary wave of amplitude A is generated between the two fixed ends x = 0 and x = L. The particle at $x = \frac{L}{3}$ is a node. There are only two particle between x $= \frac{L}{6} and x = \frac{L}{3}$ which have maximum speed half of the maximum speed of the anti-node. Again there are only two particles between x= 0 and $x = \frac{L}{6}$ which have maximum speed half of that at the antibodes. The slope of the wave function at $x = \frac{L}{3}$ changes with respect to time according to the graph shown. The symbols $μ, ω and A$ are having their usual meanings if used in calculations.

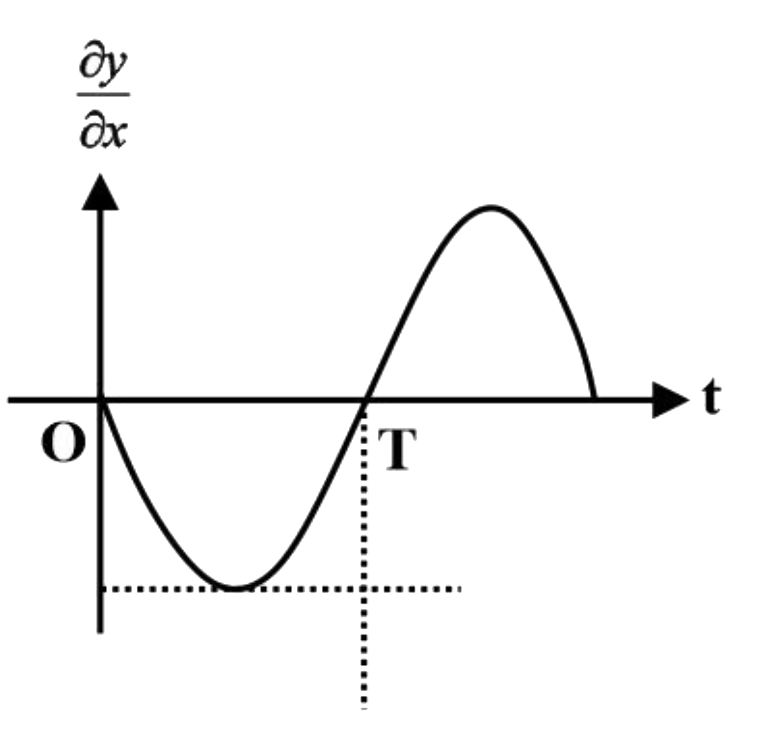
The time period of oscillations of a particle is

$\frac{T}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Answer

Step by step video, text & image solution for A stationary wave of amplitude A is generated between the two fixed ends x = 0 and x = L. The particle at x=(L)/(3) is a node. There are only two particle between x=(L)/(6) and x=(L)/(3) which have maximum speed half of the maximum speed of the anti-node. Again there are only two particles between x= 0 and x=(L)/(6) which have maximum speed half of that at the antibodes. The slope of the wave function at x=(L)/(3) changes with respect to time according to the graph shown. The symbols mu, omega and A are having their usual meanings if used in calculations. The time period of oscillations of a particle is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

If the maximum speed of a particle on a travelling wave is $v_{0}$ , then find the speed of a particle when the displacement is half of the maximum value.
A $\frac{v_{0}}{2}$
B $\frac{\sqrt{3 v_{0}}}{4}$
C $\frac{\sqrt{3 v_{0}}}{2}$
D $v_{0}$
What is the angle between the planes $2 x - y - 2 z + l = 0$ and $3 x - 4 y + 5 x - 3 = 0$ ?
A $\frac{π}{6}$
B $\frac{π}{4}$
C $\frac{π}{3}$
D $\frac{π}{2}$
The correct curve between $X_{L}$ and $log f$ is
A
B
C
D