A sound wave of wavelength λ travels towards the right horizontally with a velocity V. It strikes and reflects from a vertical plane surface , travelling at a speed v towards the left . The number of positive crests striking in a time interval of 3s on the wall is
3(V+v)/λ
3(V−v)/λ
(V+v)/3λ
(V−v)/3λ
To solve the problem, we need to find the number of positive crests of a sound wave that strike a vertical wall in a time interval of 3 seconds. Here’s a step-by-step solution:
Step 1: Understand the Relationship Between Wavelength, Velocity, and Frequency
The relationship between the speed of a wave (V), its wavelength (λ), and its frequency (f) is given by the equation:
V=f⋅λ
From this, we can express the frequency as:
f=Vλ
Step 2: Calculate the Number of Crests Striking the Wall
The number of crests that strike the wall in a given time can be calculated by multiplying the frequency of the wave by the time interval. Thus, the number of crests (N) striking the wall in time t is given by:
N=f⋅t
Substituting the expression for frequency from Step 1, we get:
N=(Vλ)⋅t
Step 3: Substitute the Given Time Interval
We are given that the time interval t=3 seconds. Therefore, we can substitute this value into our equation:
N=(Vλ)⋅3
Final Expression
Thus, the number of positive crests striking the wall in 3 seconds is:
N=3Vλ
Conclusion
The final answer for the number of positive crests striking the wall in a time interval of 3 seconds is:
N=3Vλ
---
The relationship between the speed of a wave (V), its wavelength (λ), and its frequency (f) is given by the equation:
V=f⋅λ
From this, we can express the frequency as:
f=Vλ
The number of crests that strike the wall in a given time can be calculated by multiplying the frequency of the wave by the time interval. Thus, the number of crests (N) striking the wall in time t is given by:
N=f⋅t
Substituting the expression for frequency from Step 1, we get:
N=(Vλ)⋅t
We are given that the time interval t=3 seconds. Therefore, we can substitute this value into our equation:
N=(Vλ)⋅3
Thus, the number of positive crests striking the wall in 3 seconds is:
N=3Vλ
The final answer for the number of positive crests striking the wall in a time interval of 3 seconds is:
N=3Vλ
Similar Questions
A sound wave of frequency f travels horizontally to the right . It is teflected from a larger vertical plane surface moving to left with a speed v. the speed of sound in medium is c
(a) The number of waves striking the surface per second is f(c+υ)c
(b) The wavelength of reflected wave is c(c−υ)f(c+υ)
(c) The frequency of the reflected wave is f((c+υ))(c+υ)
(d) The number of beats heard by a stationary listener to the left of the reflecting surface is υfc−υ
View Solution
A sound wave of frequency n travels horizontally to the right with speed with speed c. It is reflected from a broad wall moving to the left with speed v. The number of beats heard by a stationary observer to the left of the wall is
View Solution
Knowledge Check
A ball of mass m travelling horiozntally with velocity v strikes a massive vertical wall and rebounds back along its original direction with no change in speed. What is the magnitude of the impulse delivered by the wall to the ball?
A0B12mvCmvD2mv

A sound wave of frequency n travels horizontally to the right with speed with speed c. It is reflected from a broad wall moving to the left with speed v. The number of beats heard by a stationary observer to the left of the wall is
View SolutionA source of sound of frequency 256 Hz moves rapidly towards a wall with a velocity of 5ms−1. How many beats per second will be heard if sound travels at a speed of 330 m/s?
View SolutionA sound source emits two sinusoidal sound waves, both of wavelength λ, along paths A and B as shown in figure.The sound travelling along path B is reflected from five surfaces as shown and then merges at point Q, producing minimum intensity at that point.The minimum value of d in terms of λ is :

View SolutionIn the figure shown, light waves A and B both of wavelength λ are initially in phase and travelling rightward as incident by the two rays. Wave A is reflected from four parallel surfaces but ends up travelling in original direction. The possible value(s) of distance L in terms of wavelength λ in figure which put A and B exactly out of phase with each other after all the reflected is/are
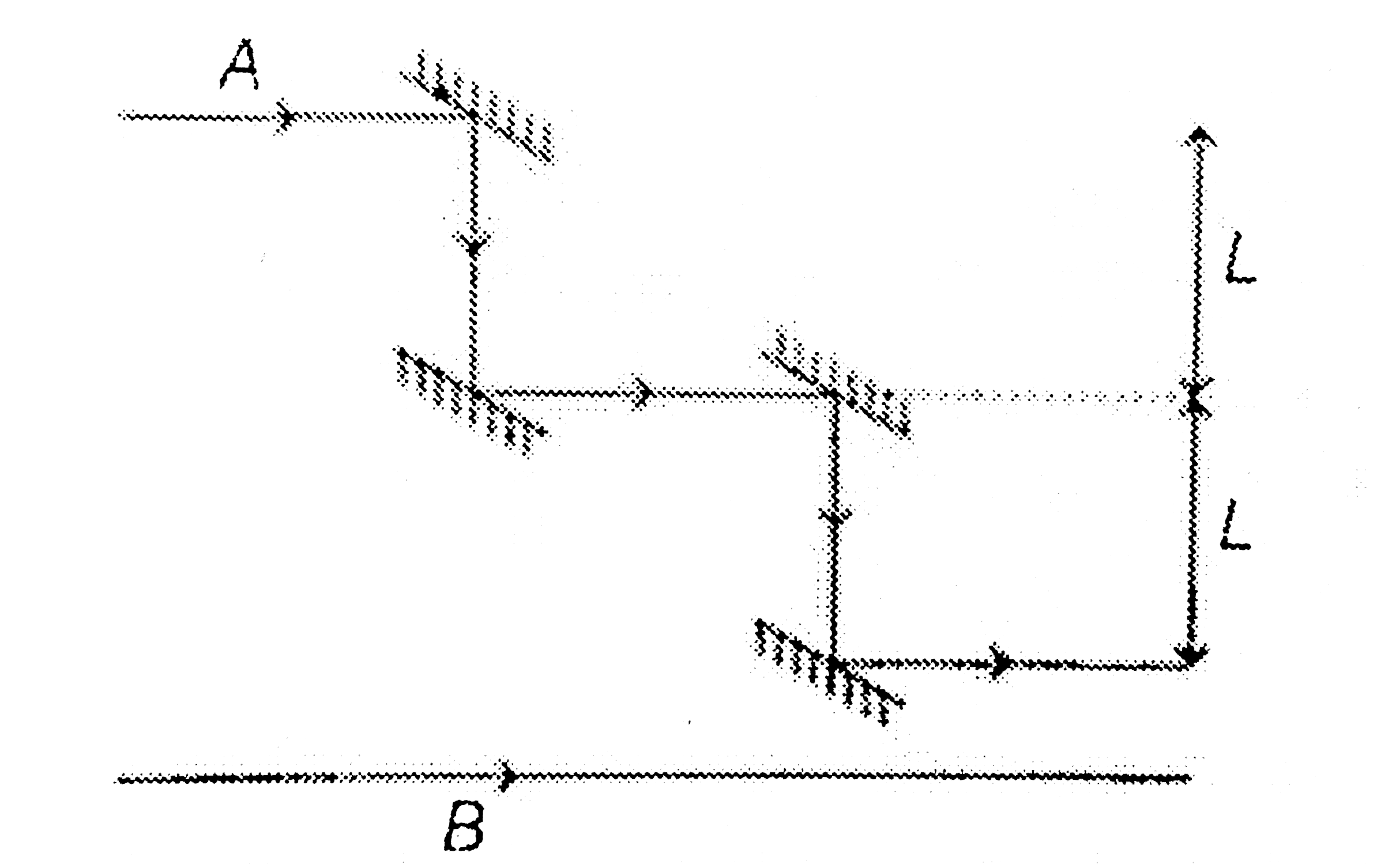
View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time

View SolutionA sound wave of frequency f propagating through air with a velocity c, is reflected from a surface which is moving away from the source with a constant speed v. Find the frequency of the reflected wave, measured by the observer at the position of the source.
View SolutionA transverse sine wave of amplitude 10 cm and wavelength 200 cm travels from left to right along a long horizontal stretched, string with a speed of 100 cm/s. Take the origin at left end of the string. At time t = 0 the left end of the string is at the origin and is moving downward. Then the equation of the wave will be ( in CGS system )
View Solution

