Area under speed-time curve gives
distance
velocity
acceleration
none of these
The correct Answer is:A
To solve the question regarding what the area under a speed-time curve represents, we can follow these steps:
1. Understanding the Graph:
- We start with a speed-time graph where the x-axis represents time (t) and the y-axis represents speed (v).
2. Identifying the Area:
- The area under the speed-time curve can be visualized as a series of rectangles (or a more complex shape depending on the graph) where the height of each rectangle corresponds to speed (v) and the width corresponds to a small time interval (dt).
3. Calculating the Area:
- The area of a small strip under the curve can be expressed as:
Area of strip=v⋅dt
- To find the total area under the curve from time t1 to t2, we integrate this expression:
Total Area=∫t2t1vdt
4. Relating Area to Distance:
- We know that speed (v) is defined as the rate of change of distance (s) with respect to time (t):
v=dsdt
- Rearranging gives us:
ds=vdt
- Therefore, integrating ds over the time interval gives us the total distance (s) traveled:
s=∫t2t1vdt
5. Conclusion:
- Hence, the area under the speed-time curve represents the total distance traveled by the body during the time interval from t1 to t2.
Final Answer:
The area under the speed-time curve gives the total distance traveled by the body.
---
- We start with a speed-time graph where the x-axis represents time (t) and the y-axis represents speed (v).
- The area under the speed-time curve can be visualized as a series of rectangles (or a more complex shape depending on the graph) where the height of each rectangle corresponds to speed (v) and the width corresponds to a small time interval (dt).
- The area of a small strip under the curve can be expressed as:
Area of strip=v⋅dt
- To find the total area under the curve from time t1 to t2, we integrate this expression:
Total Area=∫t2t1vdt
- We know that speed (v) is defined as the rate of change of distance (s) with respect to time (t):
v=dsdt
- Rearranging gives us:
ds=vdt
- Therefore, integrating ds over the time interval gives us the total distance (s) traveled:
s=∫t2t1vdt
- Hence, the area under the speed-time curve represents the total distance traveled by the body during the time interval from t1 to t2.
The area under the speed-time curve gives the total distance traveled by the body.
Similar Questions
Knowledge Check
The area under force-displacement curve represents
AvelocityBaccelerationCimpulseDwork done
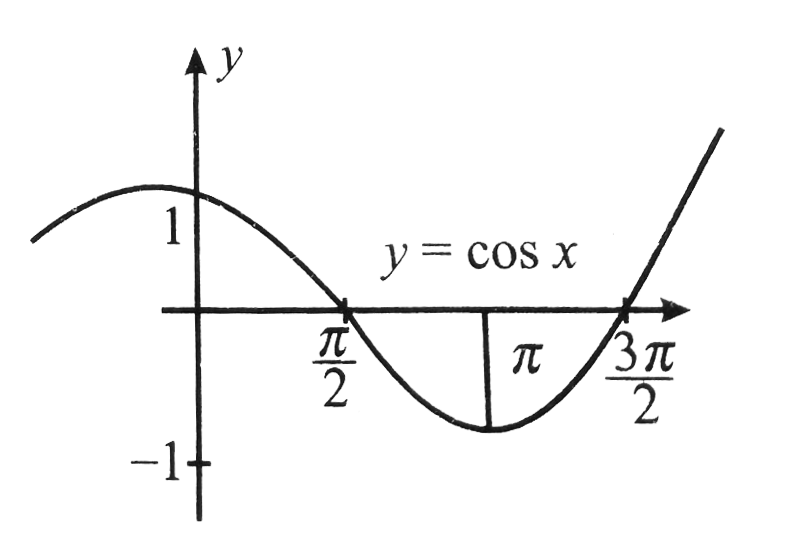
Find the area under the curve y=cosx over the interval
(a) [0,π2]
(b) [0,π]
View SolutionThe potential difference across a 2-H inductor as a function of time is shown in Fig. At time t=0, current is zero.
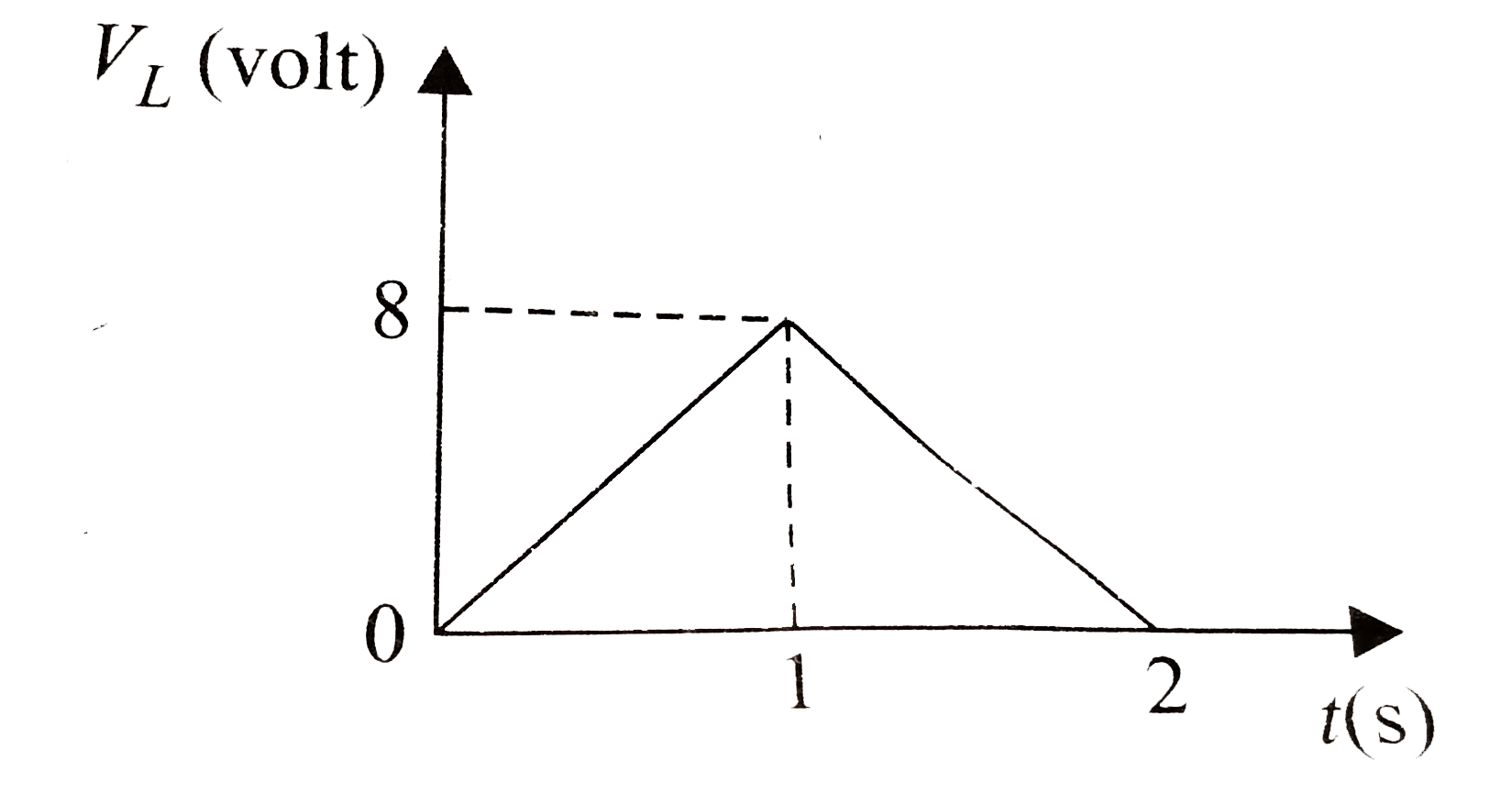
Area under VL−t graph gives
View SolutionFind the area under the curve y=sin2x+cos2x between the ordinates x = 0, x=π4
View SolutionThe spectral emissive power Eλ for a body at temperature T1 is poltted againist the wavelenght and area under the curve is found to be 9A.At a different temperature T2 the area is found to be A then λ1/λ2=
 .
.
View SolutionFind the area under the given curves and given lines:(i) y=x2,x=1,x=2and x-axis(ii) y=x4, x=1,x=5and x-axis
View SolutionThe spectra of a black body at temperatures 273∘C and 546∘C are shown in the figure. If A1 and A2 be area under the two curves respectively, the value of A2A1 is
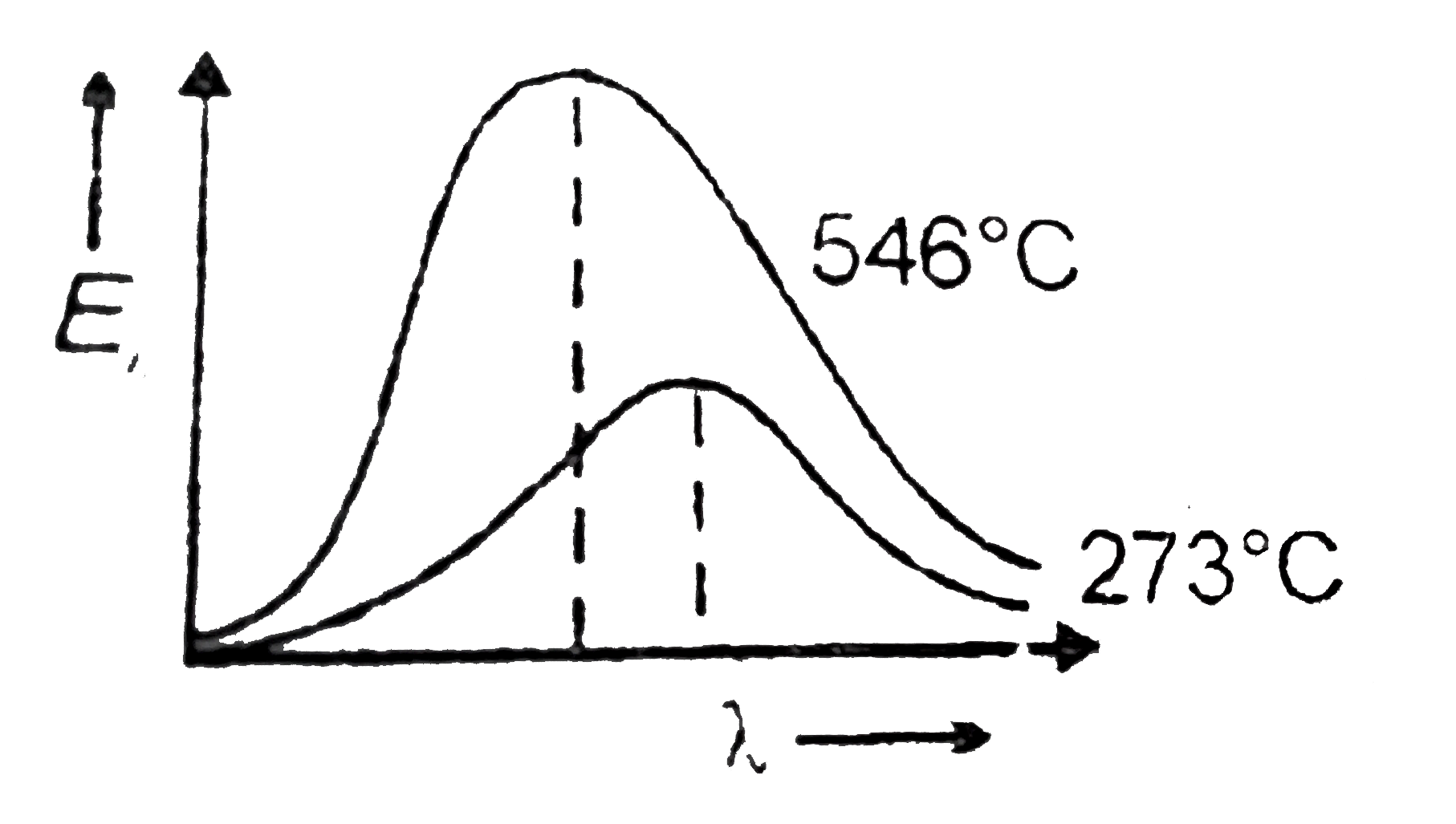
View SolutionThe spectrum of a black body at two temperatures 27∘C and 327∘C is shown in the figure. Let A1 and A2 be the areas under the two curves respectively. Find the value of A2A1
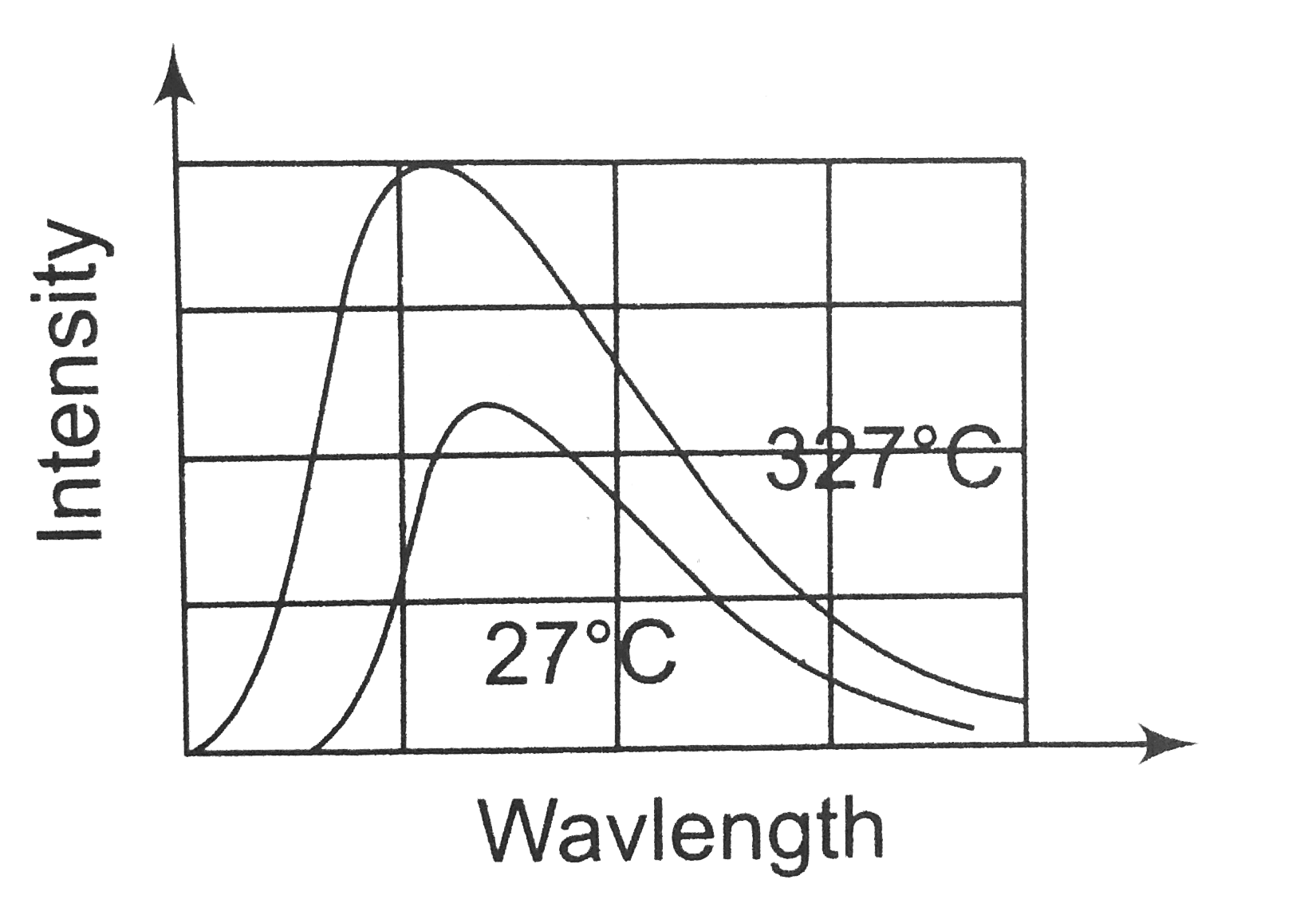
View Solution