
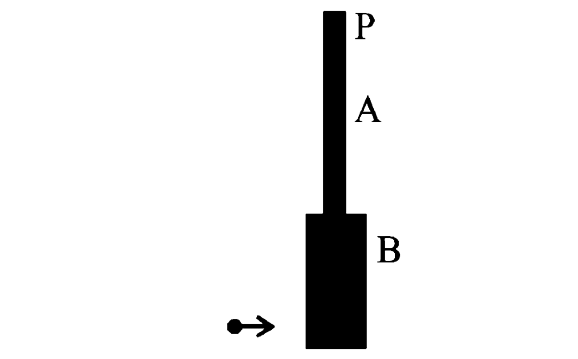
Two uniform rods A and B of length 0.6 m each and of masses 0.01 kg and 0.02 kg respectively are rigidly joined end to end the combination is pivoted at the ligher end, P as shown in figure. Such that it can freely rotate about point P in a vertical plane. A small object of mass 0.05 kg, moving horizontally, hits the lower end of the combination and sticks to it. What should be the velocity of the object, so that the system could just be raised to the horizontal position?
Moment of inertia of the system of combination of rod A and B about
P=0.01(0.6)23+(0.02)(0.6)212+0.02(0.9)2=0.018kg−m2
Moment of inertia of the object about P=(0.05)(1.2)2=0.072kg−m2
Centre of mass of the system of (A + B + small object)
=0.01×0.3+0.02×0.9+0.05×1.20.01+0.02+0.05=8.18m from the point P, and within the system.
Conserving angular momentum about P of (the rod + object) before and after collision, (0.05)(1.2)(v)=(0.072+0.018)ω, where ω is angular velocity of the system just after collision.
⇒ 0.06v=0.09ω⇒2v=3ω
Now, conservation of mechanical energy of the system, (after the collision) gives
12(0.072+0.018)ω2=0.08×8.18×10
⇒ ω=√0.08×2×8.1×108×0.09=3√2rad/s
Hence, v=3ω2=9√2=6.36m/s
Similar Questions
Two uniform thin rods A and B of length 0.6 m each and of masses 0.01 kg and 0.02kg respectively are rigidly joined end to end. The combination is pivoted at the lighter end, P as shown in fig. Such that it can freely rotate about point P in a vertical plane. A small object of mass 0.05kg, moving horizontally, hits the lower end of the combination and sticks to it what should be the velocity of the object so that the system could just be reised to the horizontal position.
View SolutionA uniform rod of mass m and length / is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity vo collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
View SolutionTwo uniform rods A and B of lengths 5 m and 3m are placed end to end. If their linear densities are 3 kg/m and 2 kg/m, the position of their centre of mass from their interface is
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

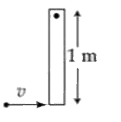
View SolutionA thin rod of mass 0.9 kg and length 1 m is suspended, at rest, from one end so that it can freely oscillate in the vertical plane. A particle of mass 0.1 kg moving in a straight line with velocity 80 m/s hits the rod at is bottom most point and sticks to it (see figure) . The angular speed ( in rad/s) of the rod immediately after the collision will be .
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is

View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionThree uniform rods, each of length 21 ( = 1m) and mass M = 8 kg are rigidly joined at their ends to form a triangular framework. Find the moment of inertia of the framework about an axis passing through the midpoints of two of its sides?
View SolutionTwo point masses of 3.0 kg and 1.0 kg are attached to opposite ends of a horizontal spring whose spring constant is 300Nm−1 as shown in the figure. The natural vibration frequency of the system is of the order of :

View Solution
