The magnitude of the gravitational field at distance r1 and r2 from the centre of a uniform, sphere of radius R and mass M are F1 and F2 respectively then-
(F1/F2)=(r1/r2) if r1<R and r2<R
(F1/F2)=(r2/r1)2 if r1>R and r2>R
(F1/F2)=(r1/r2) if r1>R and r2g<R
(F1/F2)=(r1/r2)2 if r1<R and r2<R
The correct Answer is:A, B
F∝r(r<R)
F∝1r2(r>R)
F1F2=r1r2 if r<R & F1F2=(r2r1)2 if r>R
Similar Questions
The magnitude of the gravitational field at distance r1andr_2omthecentreofaunifromsphereofradiusRandmassmareF_1 and F_2 respectively. Then:
View SolutionThe magnitude of gravitational field at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M, respectively. Find the ratio of (I1)/(I2)) if r1>R and r2>R.
View Solution
Knowledge Check
The correct plot of the magnitude of magnetic field →B vs distance r from centre of the wire is, if the radius of wire is R
A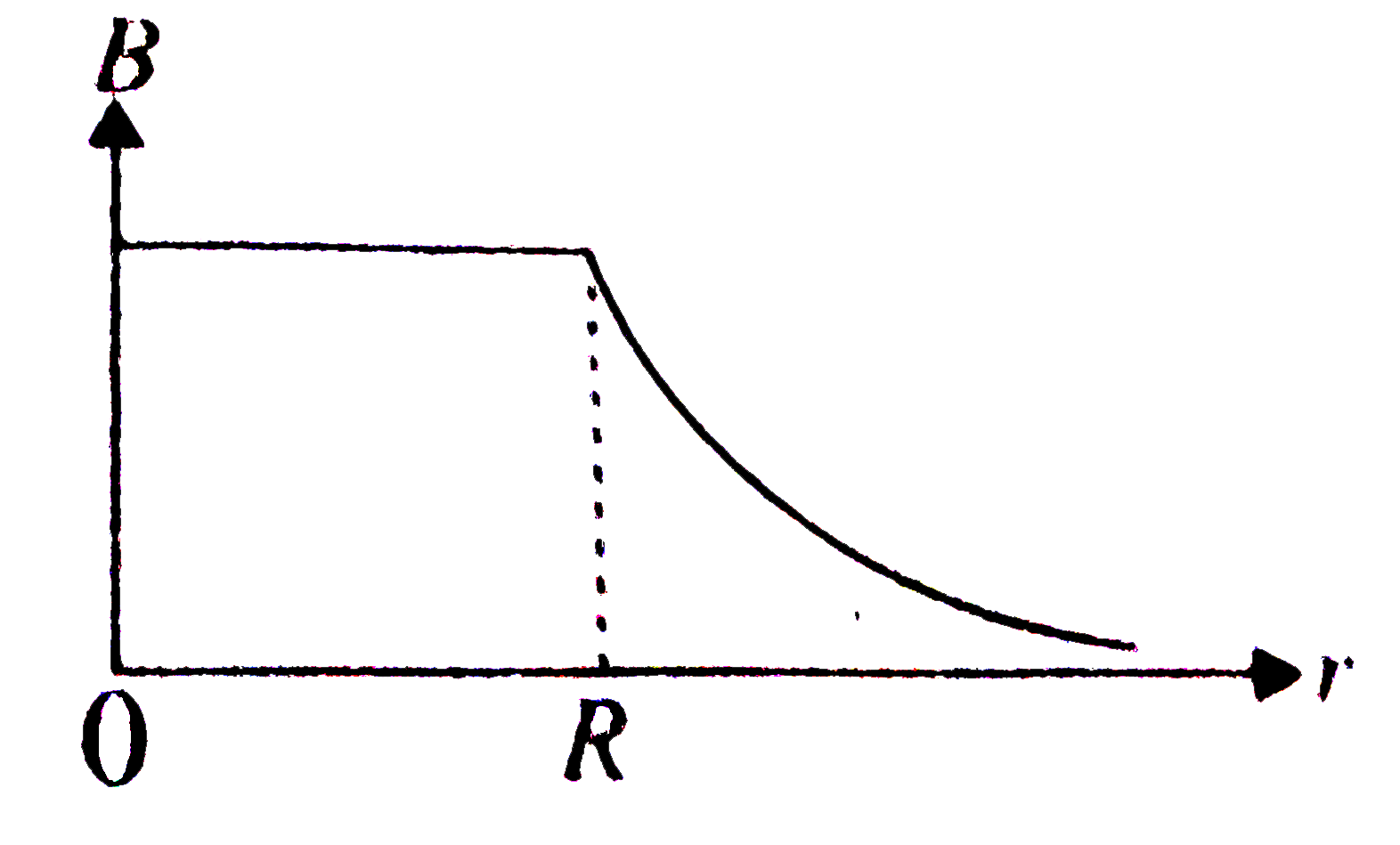 B
B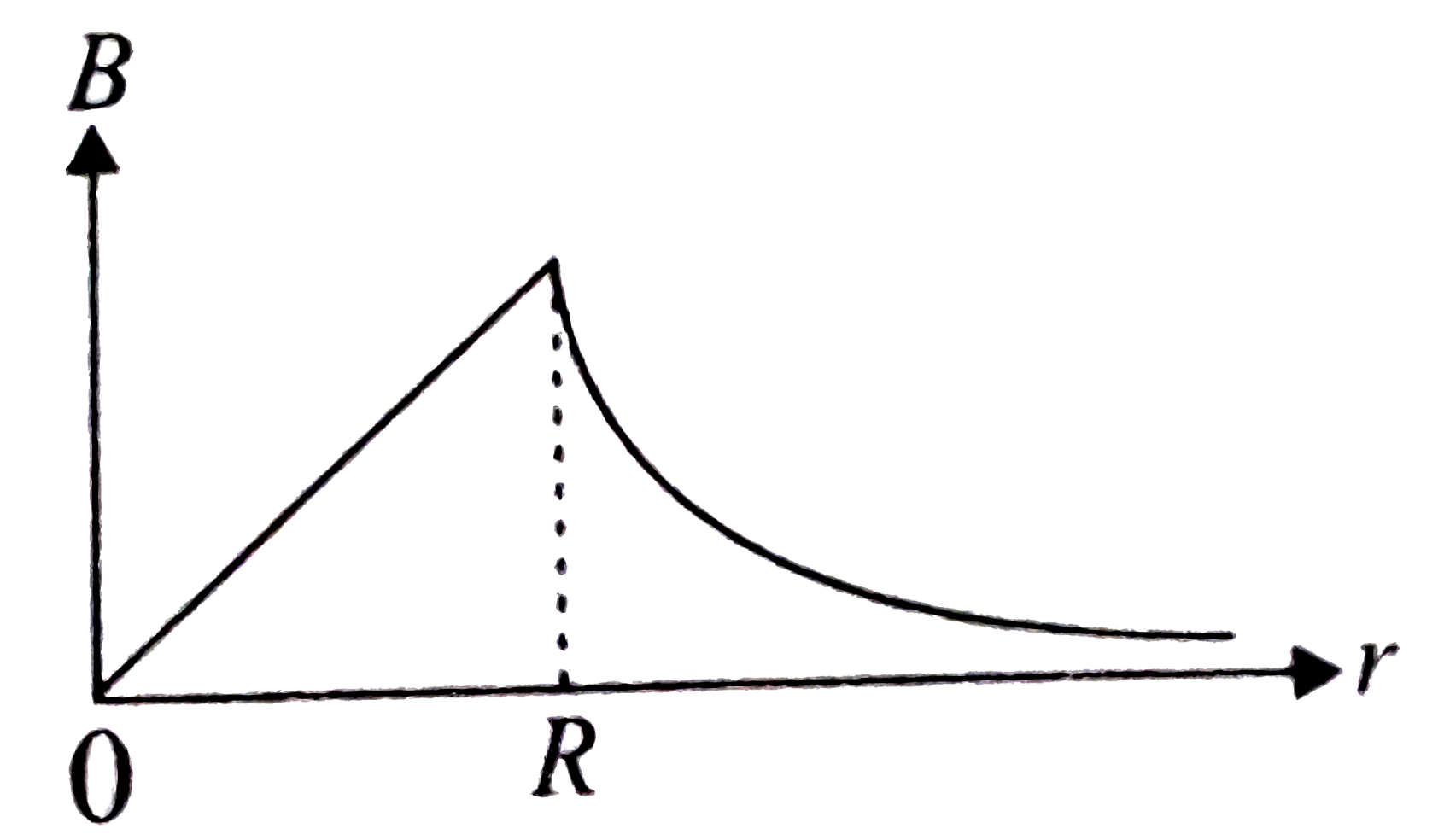 C
C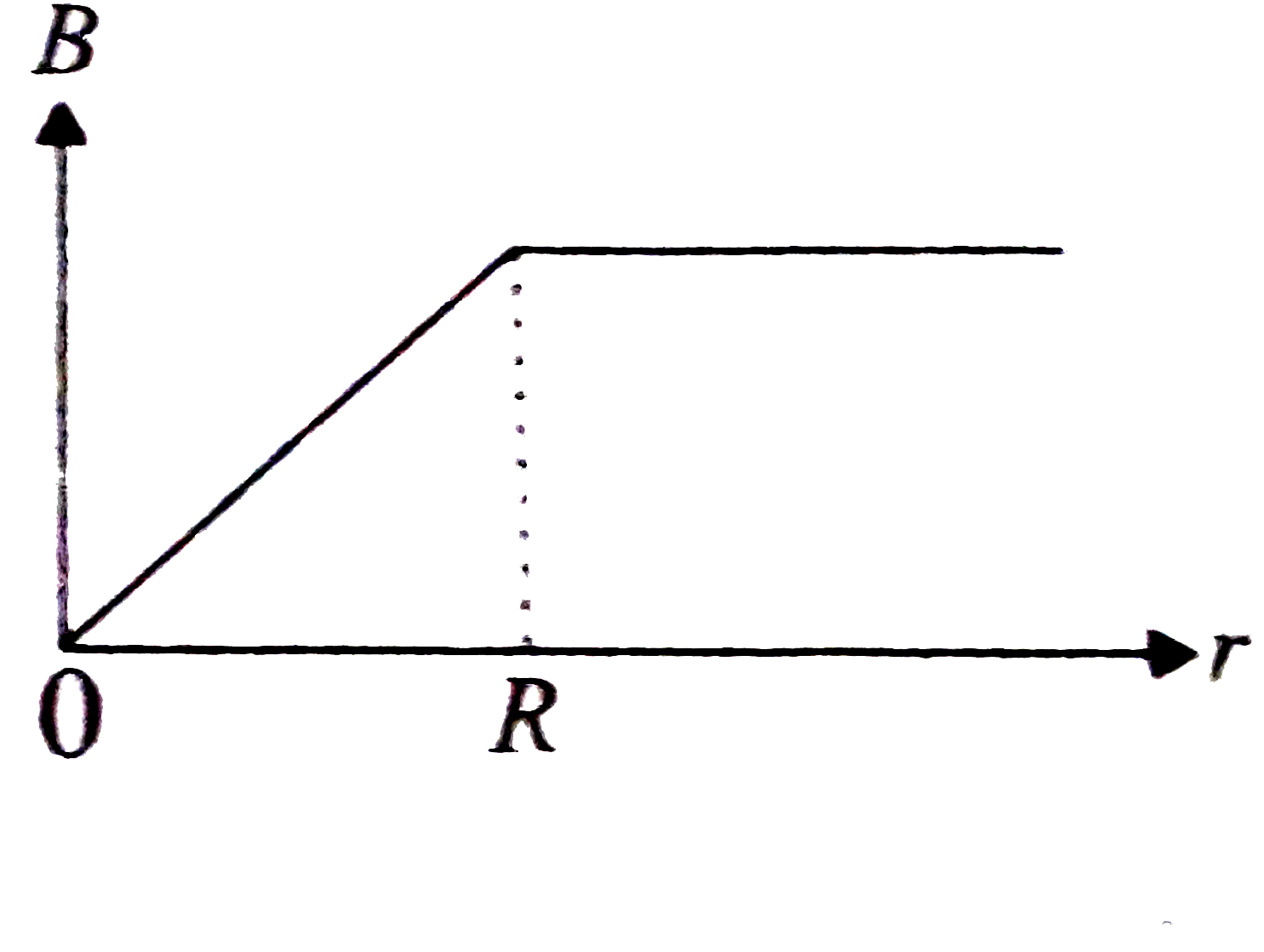 D
D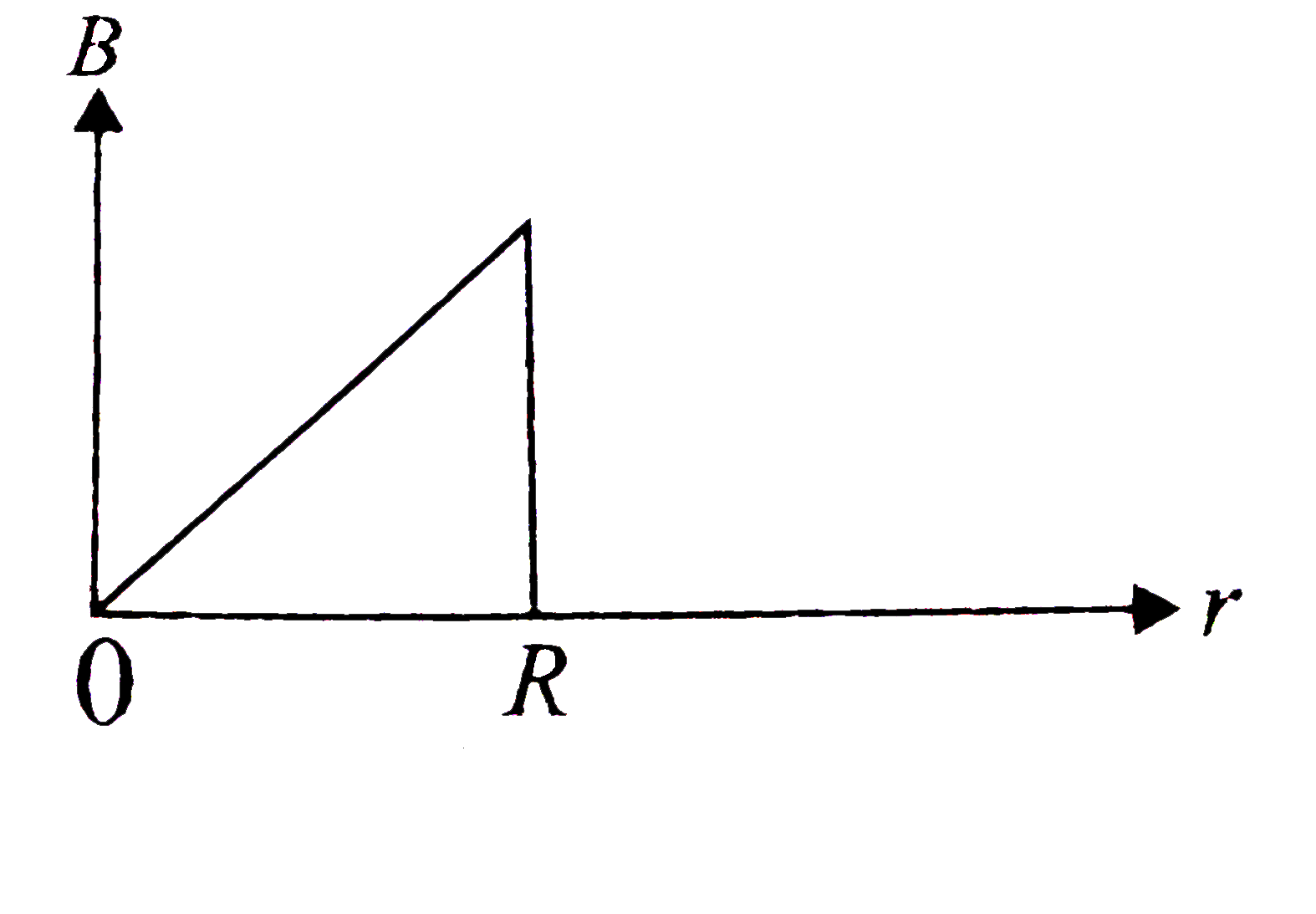
The gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View SolutionFind potential at a point 'P' at a distance 'x' on the axis away from centre of a uniform ring of mass M and radius R .
View SolutionLet V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V agasinst r is discotinuous
B. The plot of E against r is discontinuous.
View SolutionFigure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
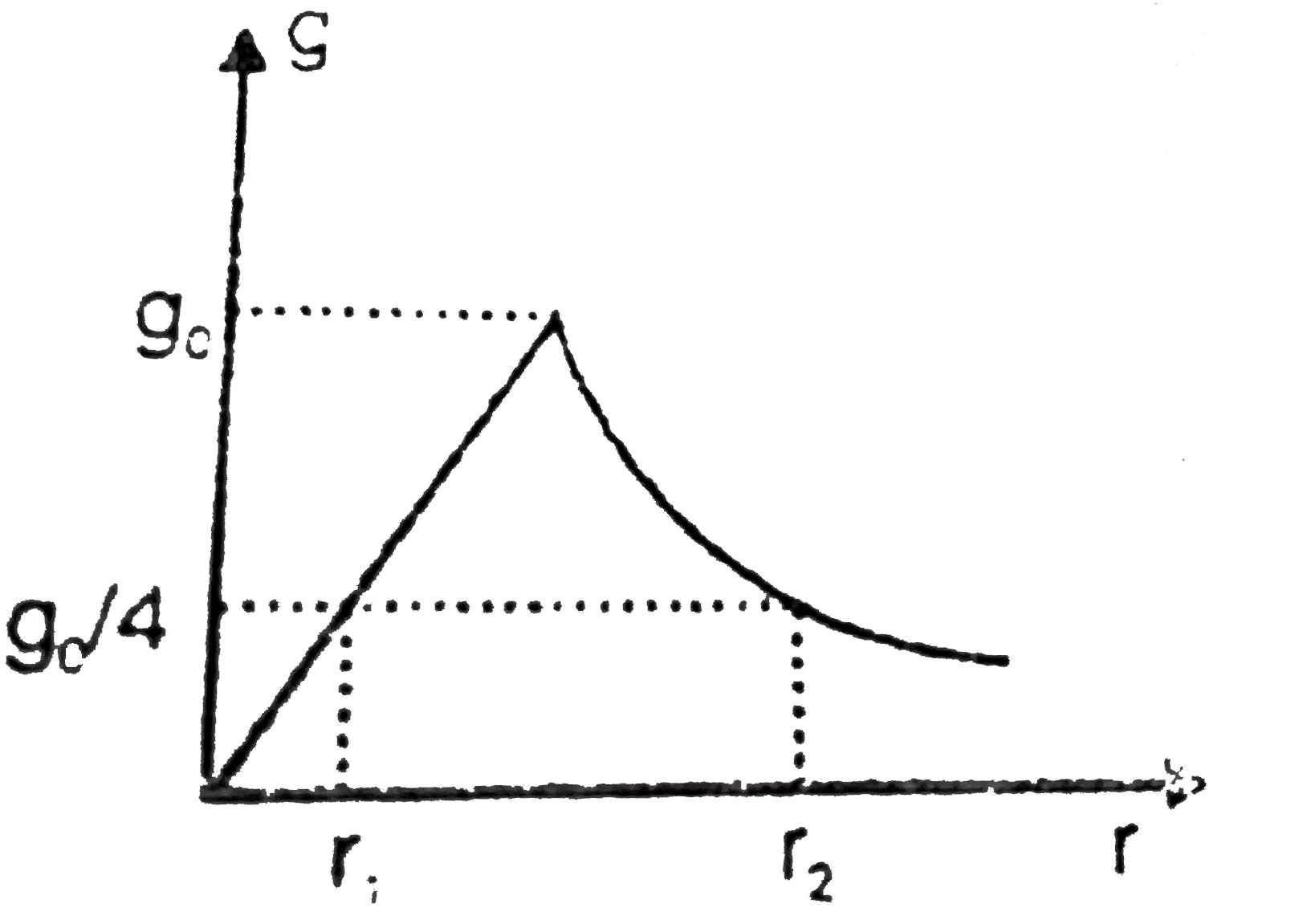
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionFollowing curve shows the variation of intesity of gravitational field (→I) with distance from the centre of solid sphere(r) :
View SolutionThe gravitational potential at a point outside the solid sphere of radius "R" and at a distance of "r" will be :
View Solution
