There are three different liquids ( liquid 1 , liquid 2 and liquid 3) having density 13.6 gm/cc ., 1.3 gm/cc and 0.8 gm/cc . Liquid 1 is poured separately into the two arms till upper surface of liquid 2 & 3 are same . What is the height of liquid 3 if height of liquid 2 is 16 cm ?
To solve the problem, we need to find the height of liquid 3 when the height of liquid 2 is given as 16 cm. We will use the principle of hydrostatic pressure, which states that at the same horizontal level, the pressure exerted by the liquids must be equal.
1. Identify the Densities:
- Density of liquid 1 (ρ₁) = 13.6 gm/cc
- Density of liquid 2 (ρ₂) = 1.3 gm/cc
- Density of liquid 3 (ρ₃) = 0.8 gm/cc
2. Define the Heights:
- Let the height of liquid 2 be h2=16 cm.
- Let the height of liquid 3 be h3 (which we need to find).
3. Set Up the Pressure Equation:
- The pressure at the same horizontal level must be equal. Thus, we can write:
PA=PB
- Where PA is the pressure at the bottom of liquid 3 and PB is the pressure at the bottom of liquid 2.
4. Calculate Pressure at Point A (Liquid 3):
- The pressure at point A (bottom of liquid 3) is given by:
PA=P0+ρ3gh3+ρ1g(H−h3)
- Here, P0 is the atmospheric pressure, g is the acceleration due to gravity, and H is the total height of liquid 1.
5. Calculate Pressure at Point B (Liquid 2):
- The pressure at point B (bottom of liquid 2) is given by:
PB=P0+ρ2gh2
6. Equate the Pressures:
- Setting PA=PB:
P0+ρ3gh3+ρ1g(H−h3)=P0+ρ2gh2
- Canceling P0 from both sides:
ρ3gh3+ρ1g(H−h3)=ρ2gh2
7. Simplify the Equation:
- Dividing the entire equation by g:
ρ3h3+ρ1(H−h3)=ρ2h2
- Rearranging gives:
ρ3h3+ρ1H−ρ1h3=ρ2h2
- Combine like terms:
(ρ3−ρ1)h3=ρ2h2−ρ1H
8. Solve for h3:
- Rearranging gives:
h3=ρ2h2−ρ1Hρ3−ρ1
9. Substituting Values:
- We know h2=16 cm, ρ1=13.6, ρ2=1.3, and ρ3=0.8:
h3=(1.3)(16)−(13.6)(H)0.8−13.6
10. Calculate the Height of Liquid 3:
- After substituting and simplifying, we find:
h3≈15.4 cm
Final Answer:
The height of liquid 3 is approximately 15.4 cm.
- Density of liquid 1 (ρ₁) = 13.6 gm/cc
- Density of liquid 2 (ρ₂) = 1.3 gm/cc
- Density of liquid 3 (ρ₃) = 0.8 gm/cc
- Let the height of liquid 2 be h2=16 cm.
- Let the height of liquid 3 be h3 (which we need to find).
- The pressure at the same horizontal level must be equal. Thus, we can write:
PA=PB
- Where PA is the pressure at the bottom of liquid 3 and PB is the pressure at the bottom of liquid 2.
- The pressure at point A (bottom of liquid 3) is given by:
PA=P0+ρ3gh3+ρ1g(H−h3)
- Here, P0 is the atmospheric pressure, g is the acceleration due to gravity, and H is the total height of liquid 1.
- The pressure at point B (bottom of liquid 2) is given by:
PB=P0+ρ2gh2
- Setting PA=PB:
P0+ρ3gh3+ρ1g(H−h3)=P0+ρ2gh2
- Canceling P0 from both sides:
ρ3gh3+ρ1g(H−h3)=ρ2gh2
- Dividing the entire equation by g:
ρ3h3+ρ1(H−h3)=ρ2h2
- Rearranging gives:
ρ3h3+ρ1H−ρ1h3=ρ2h2
- Combine like terms:
(ρ3−ρ1)h3=ρ2h2−ρ1H
- Rearranging gives:
h3=ρ2h2−ρ1Hρ3−ρ1
- We know h2=16 cm, ρ1=13.6, ρ2=1.3, and ρ3=0.8:
h3=(1.3)(16)−(13.6)(H)0.8−13.6
- After substituting and simplifying, we find:
h3≈15.4 cm
The height of liquid 3 is approximately 15.4 cm.
Similar Questions
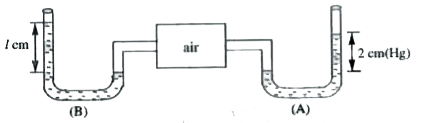
What is l if the liquid in manometre 'B' has a density 1.36 gm/cc.
View SolutionA liquid X of density 3.36g/cm3 poured in a U-tube which contains Hg. Another liquid Y is poured in left arm with heght 8 cm upper levels of X and Y are same. What is density of Y?
View SolutionHow many molecule are present in 12 L of liquid CCl4? The density of the liquid is 1.59 g cm−3?
View SolutionA cubical tank of side 1 m is filled with 800 kg of a liquid. Find the density of liquid in kg m−3
View SolutionProve that the average pressure of a liquid (density ρ) on the walls of the container filled upto height h with liquid is 12hρg.
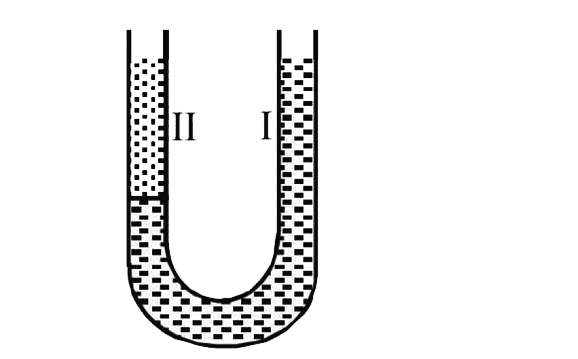
View SolutionA U-tube of uniform cross section (see figure) is partially filled with a liquid I. Another liquid II which does not mix with liquid I is poured into one side. It is found that the liquid levels of the two sides of the tube are the same, while the level of liquid I has risen by 2cm. If the specific gravity of liquid I is 1.1, the specific gravity of liquid II must be
View SolutionThe vapour pressure of a liquid in a closed container depends upon (1) temperature of liquid (2) quantity of liquid (3) surface area of the liquid
View SolutionTwo miscible liquids of densities 1.2gm/cm and 1.4gm/cm aer mixed with a proportion ratio of their volumes equal to 2.5: what is the density of redulting liquid?
View SolutionA coaxial cylinder made of glass is immersed in a-liquid of surface tension S. The radius of the inner and outer surface of the cylinder are R1andR2 respectively . Height till which liquid will rise is (Density of liquid is ρ )
View SolutionA body weighs W1 in a liquid of density ρ1 and W2 in a liquid of density ρ2. What is the weight of body in a liquid of density ρ3?
View Solution
