The ratio of the radius of the tube of a venturimeter is η(η>1) . The ratio of the densities of the liquid in the manometer and the moving fluid is η1 . If the difference in heights of the liquid column in the manometer is h , find the minimum speed of flow of the fluid .
To solve the problem, we will use the principles of fluid mechanics, specifically Bernoulli's equation and the continuity equation. Let's break down the solution step by step.
Step 1: Understand the given ratios
We are given:
- The ratio of the radius of the tube of a venturimeter: η (where η>1)
- The ratio of the densities of the liquid in the manometer and the moving fluid: η1
- The height difference in the manometer: h
Step 2: Relate the areas of the venturimeter
The area A of a circular tube is given by:
A=πr2
If the radius of the larger section is R and the smaller section is r, then:
R=ηr
Thus, the areas are:
A1=πr2(smaller section)
A2=πR2=π(ηr)2=πη2r2(larger section)
Step 3: Apply the continuity equation
According to the continuity equation, the product of the area and velocity at two points in a streamline flow is constant:
A1v1=A2v2
Substituting the areas:
πr2v1=πη2r2v2
Cancelling πr2 (assuming r≠0):
v1=η2v2
Step 4: Apply Bernoulli's equation
Using Bernoulli's equation between the two sections, we have:
P1+12ρ1v21=P2+12ρ2v22
Where:
- P1 is the pressure at the larger section
- P2 is the pressure at the smaller section
- ρ1 is the density of the liquid in the manometer
- ρ2 is the density of the moving fluid
Step 5: Relate pressures using the manometer
The pressure difference can be expressed using the height difference h:
P1−P2=ρ1gh
Substituting this into Bernoulli's equation gives:
ρ1gh=P2−P1+12ρ2v22−12ρ1v21
Step 6: Substitute v1 in terms of v2
Substituting v1=η2v2 into the equation:
ρ1gh=12ρ2v22−12ρ1(η2v2)2
This simplifies to:
ρ1gh=12ρ2v22−12ρ1η4v22
Factoring out v22:
ρ1gh=12v22(ρ2−ρ1η4)
Step 7: Solve for v2
Rearranging gives:
v22=2ρ1ghρ2−ρ1η4
Taking the square root:
v2=√2ρ1ghρ2−ρ1η4
Step 8: Find the minimum speed of flow
To find the minimum speed of flow v in terms of v2:
Using the relation v=v2η2:
v=1η2√2ρ1ghρ2−ρ1η4
Final Expression
Substituting ρ2=η1ρ1:
v=√2η1ghη4−1
Conclusion
The minimum speed of flow of the fluid is:
v=√2η1ghη4−1
We are given:
- The ratio of the radius of the tube of a venturimeter: η (where η>1)
- The ratio of the densities of the liquid in the manometer and the moving fluid: η1
- The height difference in the manometer: h
The area A of a circular tube is given by:
A=πr2
If the radius of the larger section is R and the smaller section is r, then:
R=ηr
Thus, the areas are:
A1=πr2(smaller section)
A2=πR2=π(ηr)2=πη2r2(larger section)
According to the continuity equation, the product of the area and velocity at two points in a streamline flow is constant:
A1v1=A2v2
Substituting the areas:
πr2v1=πη2r2v2
Cancelling πr2 (assuming r≠0):
v1=η2v2
Using Bernoulli's equation between the two sections, we have:
P1+12ρ1v21=P2+12ρ2v22
Where:
- P1 is the pressure at the larger section
- P2 is the pressure at the smaller section
- ρ1 is the density of the liquid in the manometer
- ρ2 is the density of the moving fluid
The pressure difference can be expressed using the height difference h:
P1−P2=ρ1gh
Substituting this into Bernoulli's equation gives:
ρ1gh=P2−P1+12ρ2v22−12ρ1v21
Substituting v1=η2v2 into the equation:
ρ1gh=12ρ2v22−12ρ1(η2v2)2
This simplifies to:
ρ1gh=12ρ2v22−12ρ1η4v22
Factoring out v22:
ρ1gh=12v22(ρ2−ρ1η4)
Rearranging gives:
v22=2ρ1ghρ2−ρ1η4
Taking the square root:
v2=√2ρ1ghρ2−ρ1η4
To find the minimum speed of flow v in terms of v2:
Using the relation v=v2η2:
v=1η2√2ρ1ghρ2−ρ1η4
Substituting ρ2=η1ρ1:
v=√2η1ghη4−1
The minimum speed of flow of the fluid is:
v=√2η1ghη4−1
Similar Questions
A vertical U-tube has two liquids 1 and 2. The heights of liquids columns in both the limbs are h and 2h, as shown in the figure. If the density of the liquid 1 is 2ρ.
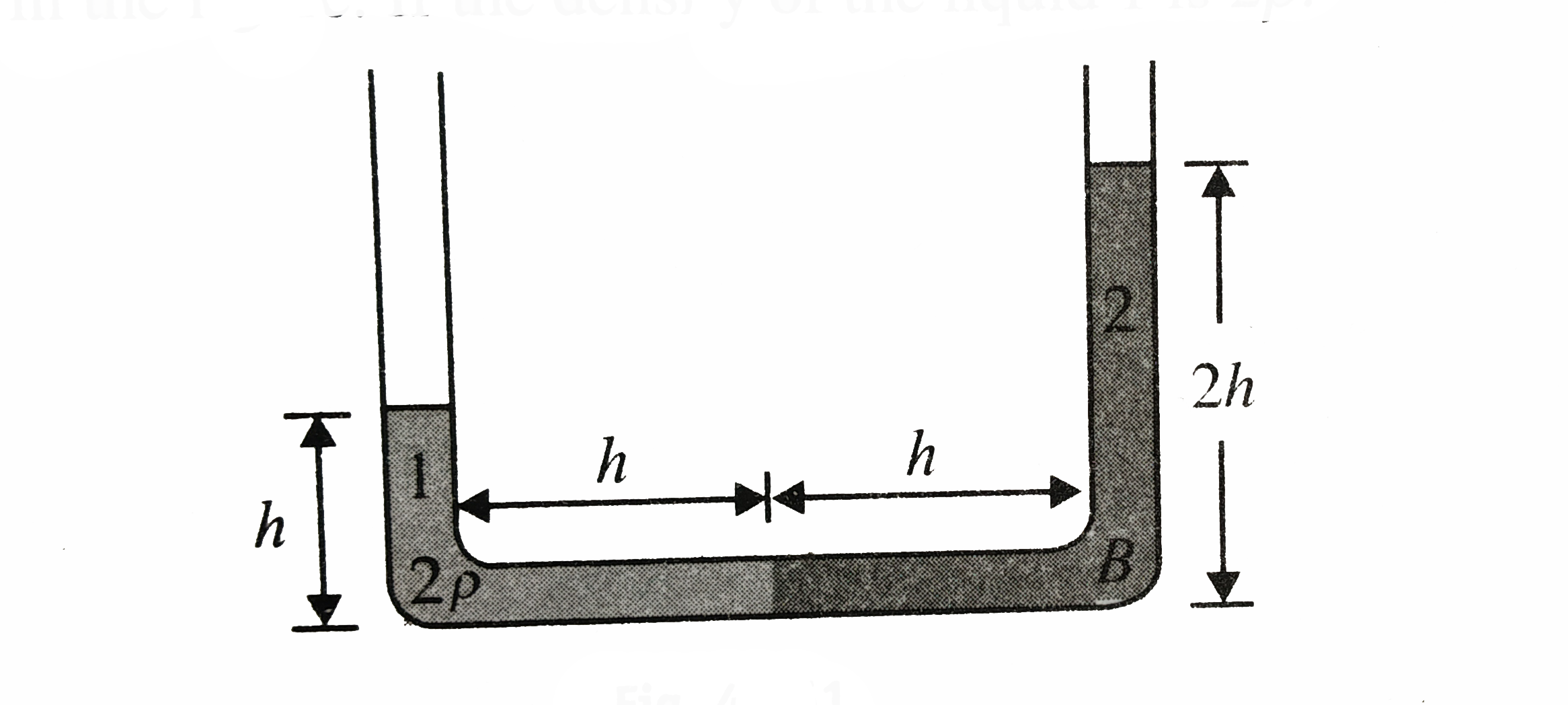
a. Find the density of liquid 2.
b. If we accelerate the tube towards right till the heights of liquid columns will be the same, find the acceleration of the tube.
View SolutionA U tube is rotated about one of it's limbs with an angular velocity ω. Find the difference in height H of the liquid (density ρ) level, where diameter of the tube d<<L.
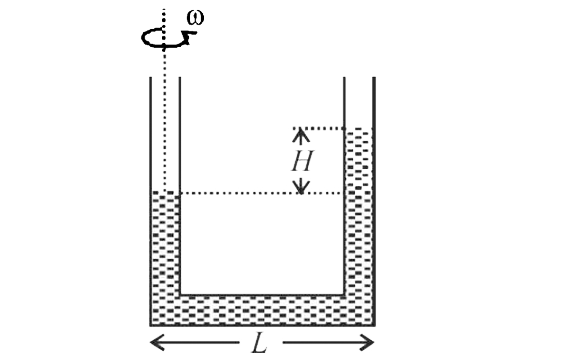
View SolutionWater is used as the manometric liquid in a pitot tube mounted in an aircraft to measure air speed. If the maximum difference in height between the liquid columns is 0.1m, what is the maximum air speed that can be measured? Density of air ddir=1.3kg/m3
View Solutionq=12nv2
The dynamic pressure q generated by a fluid moving with velocity v can be found using the formula above, where n is the constant density of the fluid. An aeronautical engineer uses the formula to find the dynamic pressure of a fluid moving with velocity v and the same fluid moving with velocity 1.5v. What is the ratio of the dynamic pressure of the faster fluid to the dynamic pressure of the slower fluid?
View SolutionA liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then

View SolutionA horizontal tube has different cross sections at points A and B. The areas of cross section are a1 and a2 respectively, and pressures at these points are p1=ρgh1 and p2=ρgh2 where ρ is the density of liquid flowing in the tube and h1 and h2 are heights of liquid columns in vertical tubes connected at A and B. If h1−h2=h, then the flow rate of the liquid in the horizontal tube is
View SolutionA vertical U-tube has a liquid up to a height h. If the tube is slowly rotated to an angular speed ω=√gh find the (i) heights of the liquid column, ii pressures at the points 1,2 and 3 in the limbs in steady state.

View SolutionWater flows through a tunnel from the reservior of a dam towards the turbine installed in its power plant . The power plant is situated h metre below the reservoir . If the ratio of the cross sectional areas of the tunnel at the resercoir and power station end is η , find the speed of the water entering into the turbine .
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
Situation II:
A cyliner is removed and the original arrangement is restoreed.A tiny hole of area s(s<<A) is punched on the veritical side of the containier at a height h(h<H/2)
The height hm at which the hole should be punched so that the liquid travels the maximum distance is
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the Body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
Situation I:
A homogeneous solid cylinder of length L(L<H/2). cross sectional area A/5 is immersed such that it floats with its axis vertical at liquid -liquid interface with lenght L/4 in the denser liquid.
The density of the solid is
View Solution

