Water flows through a tunnel from the reservior of a dam towards the turbine installed in its power plant . The power plant is situated h metre below the reservoir . If the ratio of the cross sectional areas of the tunnel at the resercoir and power station end is η , find the speed of the water entering into the turbine .
To solve the problem, we will use the principles of fluid mechanics, specifically the continuity equation and Bernoulli's equation.
1. Identify the Variables:
- Let h be the height difference between the reservoir and the turbine.
- Let A1 be the cross-sectional area of the tunnel at the reservoir.
- Let A2 be the cross-sectional area of the tunnel at the turbine.
- Let η=A1A2 be the ratio of the areas.
- Let V1 be the velocity of water at the reservoir.
- Let V2 be the velocity of water at the turbine.
2. Apply the Continuity Equation:
The continuity equation states that the flow rate must be constant, which gives us:
A1V1=A2V2
From this, we can express V1 in terms of V2:
V1=A2A1V2=V2η
3. Apply Bernoulli's Equation:
According to Bernoulli's principle, for points 1 (reservoir) and 2 (turbine):
P1ρg+V212g+z1=P2ρg+V222g+z2
Since both points are at atmospheric pressure, P1=P2, and we can cancel these terms out. Let z1=h and z2=0:
h+V212g=V222g
4. Rearranging the Equation:
Rearranging gives us:
h=V222g−V212g
Substituting V1=V2η:
h=V222g−12g(V2η)2
This simplifies to:
h=V222g−V222gη2
Factoring out V222g:
h=V222g(1−1η2)
5. Solving for V2:
Rearranging gives:
V22=2gh1−1η2
Thus, taking the square root:
V2=
⎷2gh1−1η2
6. Final Expression:
We can express this as:
V2=√2ghη2η2−1
Final Answer:
The speed of the water entering into the turbine is:
V2=√2ghη2η2−1
- Let h be the height difference between the reservoir and the turbine.
- Let A1 be the cross-sectional area of the tunnel at the reservoir.
- Let A2 be the cross-sectional area of the tunnel at the turbine.
- Let η=A1A2 be the ratio of the areas.
- Let V1 be the velocity of water at the reservoir.
- Let V2 be the velocity of water at the turbine.
The continuity equation states that the flow rate must be constant, which gives us:
A1V1=A2V2
From this, we can express V1 in terms of V2:
V1=A2A1V2=V2η
According to Bernoulli's principle, for points 1 (reservoir) and 2 (turbine):
P1ρg+V212g+z1=P2ρg+V222g+z2
Since both points are at atmospheric pressure, P1=P2, and we can cancel these terms out. Let z1=h and z2=0:
h+V212g=V222g
Rearranging gives us:
h=V222g−V212g
Substituting V1=V2η:
h=V222g−12g(V2η)2
This simplifies to:
h=V222g−V222gη2
Factoring out V222g:
h=V222g(1−1η2)
Rearranging gives:
V22=2gh1−1η2
Thus, taking the square root:
V2=
⎷2gh1−1η2
We can express this as:
V2=√2ghη2η2−1
The speed of the water entering into the turbine is:
V2=√2ghη2η2−1
Similar Questions
At a hydroelectric power plant, water is directed at high speed against turbine blades on an axle that turns an electric generatior. For maximum power generation, should the turbine blades be desigened so that the water is brought to a dead stop, or so that the water rebounds?
View SolutionWater flows through a horizontal tube of variable cross section.The area of cross section at A and B are 4 mm2and2mm2 respectively. If 1 cc of water enters per second through A find
a) The speed of water at A
b) the speed of river at B
c) the pressure difference PA−PB.

View Solution(a) Draw the diagram of a device which is used to decrease high S voltage into a AC voltage and state its working principle. Write four sources of energy loss in this device.
(b) A small town with a demand of 1200 kW of electric power at 220 V is situated 20 Km away from an electric plant generating power at 440V. The resistance of the two wire line carrying power is 0.5Ω per km. The town gets the power from the line through a 4000-220 V step-down transformer at s sub-station in the town. Estimate the line power loss in the from of heat.
View SolutionA dam is situated at a height of 300 m above sea level. It supplies water to a power house which is at a height of 60m above sea level. 1000kg of water passes through the turbine per second. If the efficiency of the system is 80% the electrical power out is
View SolutionA dam is situated at a height of 300 m above sea level. It supplies water to a power house which is at a height of 60m above sea level. 1000kg of water passes through the turbine per second. If the efficiency of the system is 80% the electrical power out is
View SolutionWater flows through a horizontal tube of variable cross-section. The area of cross section at A and B are 4mm2and2mm2 respectively. If 1 cc of water enters per seconds through. A find a. The speed of water at A, b. the speed of river at B and c. the pressure difference PA−PB.

View SolutionA dam is situated at a height of 550m above sea level and supplies water to a power house which is at a height of 50m above sea level. 2000kg of water passes through the turbines per second. What would be the maximum electrical power output (in MW) os the power house if the whole system were 60% efficent ?
View SolutionAt a hydroelectric power plant, the water pressure head is at a height of 300 m and the water flow available is 100m3s−1. If the turbine generator efficiency is 60%, estimate the electric power available from the plant (g=9.8ms−2).
View Solution
In a certain pump whose rated power is P. ideal fluid of denstiy ρ enters with speed V0 which lifts water upto height h through a pipe of uniform cross section area without discontinuity. Volumetric flow rate of the liquid is Q. Speed of fluid when it comes out of the pipe at point A is (Assume that pump works at 100 % efficiency and flow is streamline)
View SolutionElectric fuse is a protective device used in series with an electric circuit or an electric appliance to save it from damage due to overheating porduced by strong current in the circuit or application. Fuse wire is generally made from an alloy of lead and tin, which has hifh resistance and low melting point. It is connected in series in an electric installation. If a circuit gets accidentally short-circuited, a large current flows, then fuse wire melts away, which causes a break in the circuit. The power through fuse (F') is equal to heat energy lost per unit area per unit time (h) (neglecting heat loses from ends of the wire).
P=I2R=h×2πrl[R=ρlπr2]
where r and l are the length and radius of fuse wire, respectively.
A Battery is described by its emf (E) and internal resistance (r). Efficiency of battery (η) is defined as the ratio of the output to the input power.
η=OutputpowerInputpower×100%
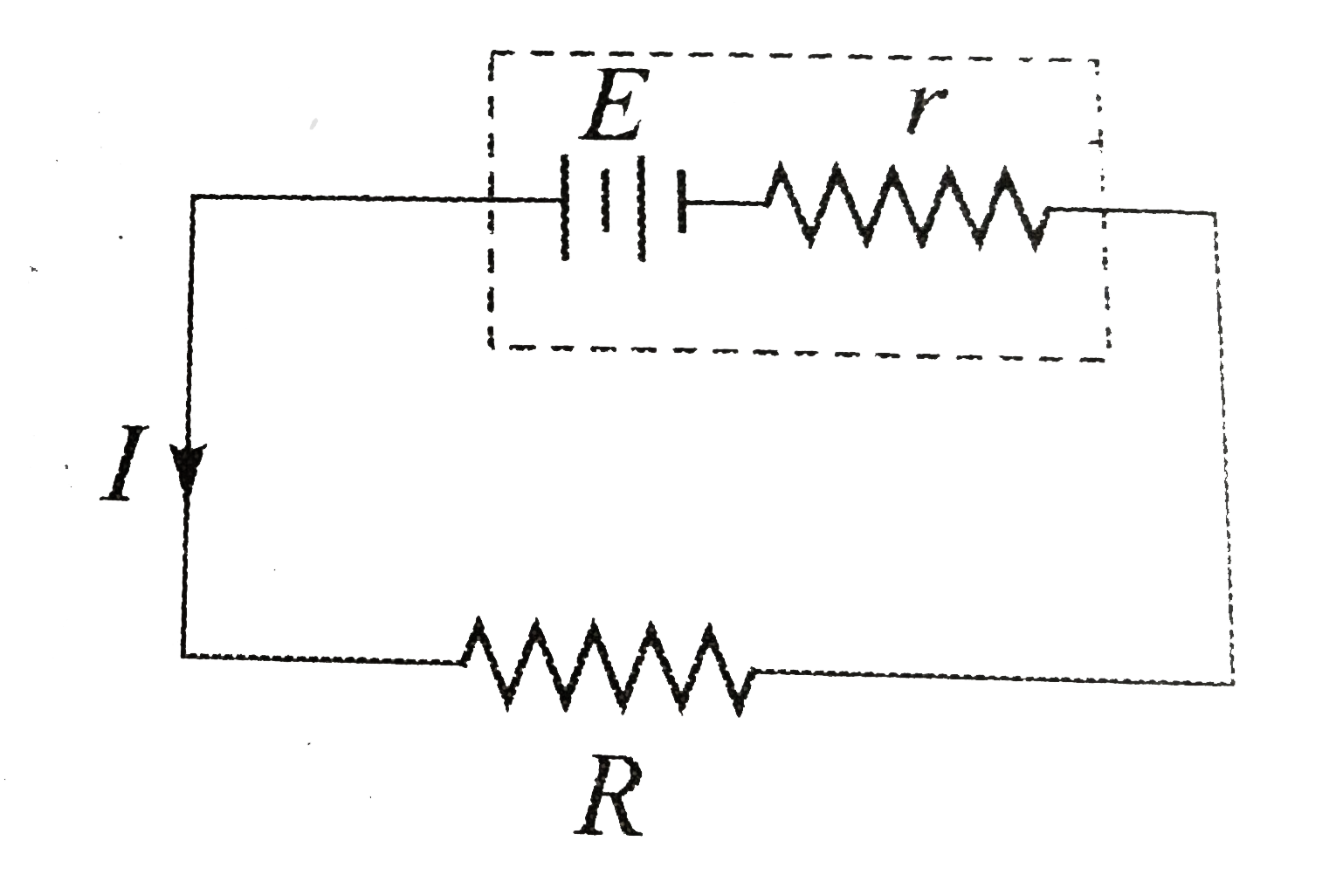
But I=E/(R+r), input power = EI.
Output power =EI−I2r, then.
η=(EI−I2rEI)×100=(1−IrE)×100
=[1−(ER+r)(rE)]×100=(RR+r)×100
We know that output power of a source is maximum when the external resistance is equal to internal resistance, i.e., R = r .
Two fuse wires of same potential , material have length ratio 1:2 and ratio of radius 4:1. Then respective ratio of their current rating will be
View Solution
