A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is:

Consider a differential area of width dy and length b at a depth y from the free surface of liquid .
dF=(P0lρgy) (bdy )
F=∫h0(P0+ρgy)(bdy)=P0bh+pgbh22

Similar Questions
Knowledge Check
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρ
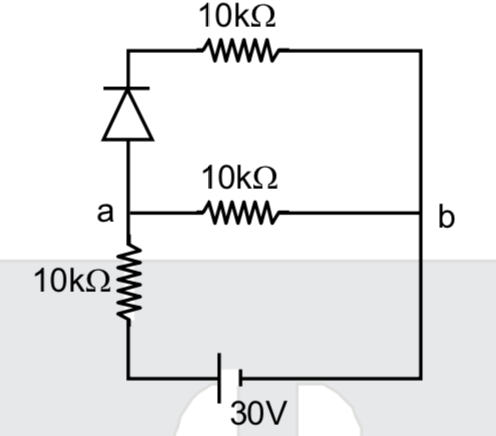
There is a electric circuit as shown in the figure. Find potential difference between points a and b.
View SolutionFigure shows a siphon. The liquid shown in water. The pressure difference PB−PA between the points A and B is

View SolutionA liquid kept in a container has a horizontal acceleration 'a' as shown in figure.
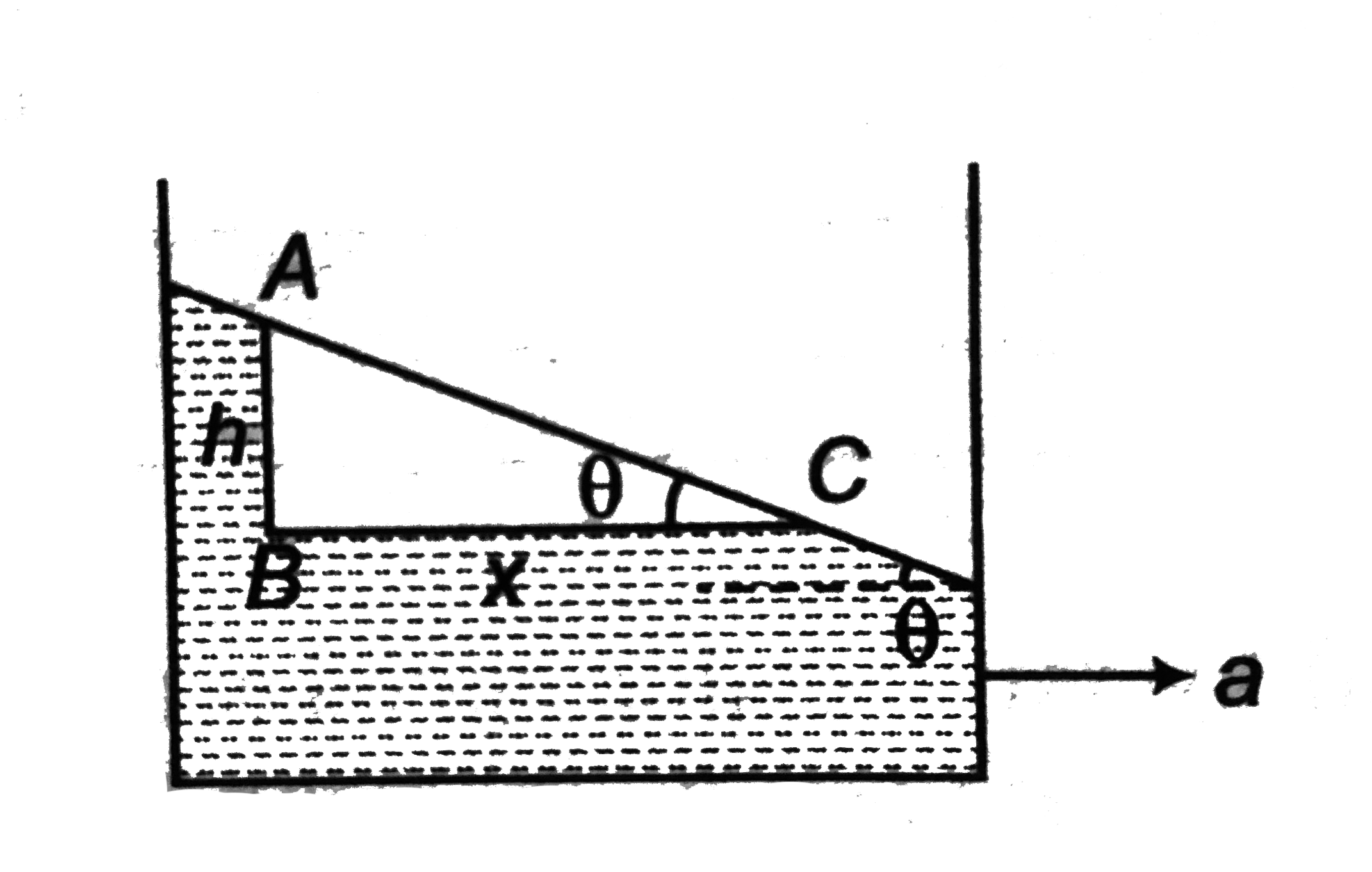
Using the pressure equation along the path ABC find the angle θ.
View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
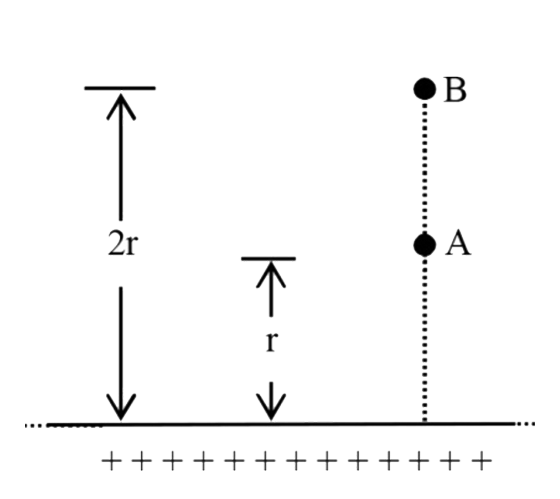
View SolutionAn infinitely long line of linear charge density λ is shown in the figure. The potential difference VA−VB between the two points A and B is
View SolutionA U-tube of base length l filled with the same volume of two liquids of densities ρ and 2ρ is moving with an acceleration 'a' on the horizontal plane. If the height difference between the two surfaces (open to atmosphere) becomes zero, then the height h is given by

View SolutionA ball of density ais released from rest from the centre of an accelerating sealed cubical vessel completely filled with a liquid of density ρ. If the trough moves with a horizontal acceleration →a0 find the initial acceleration of the ball.
View Solution