Find the work done by an external agent in lowering a block of mass m slowly on a fixed light spring of stiffness k, till it comes to rest.
To find the work done by an external agent in lowering a block of mass m slowly on a fixed light spring of stiffness k until it comes to rest, we can follow these steps:
Step 1: Understanding the Forces Involved
When the block is lowered slowly, the forces acting on it are:
- The gravitational force Fg=mg acting downward.
- The spring force Fs=kx acting upward, where x is the compression of the spring.
Step 2: Setting Up the Equation of Motion
Since the block is lowered slowly, it moves with zero acceleration. Therefore, the net force acting on the block is zero:
Fg−Fs=0⟹mg−kx=0
From this, we can express the compression of the spring x in terms of m and k:
kx=mg⟹x=mgk
Step 3: Calculating the Work Done by Gravity
The work done by gravity when the block is lowered by a distance x is given by:
Wg=mgh
Substituting h with x:
Wg=mgx=mg(mgk)=m2g2k
Step 4: Calculating the Work Done by the Spring
The work done by the spring when it is compressed by a distance x is given by:
Ws=−12kx2
Substituting x:
Ws=−12k(mgk)2=−12k(m2g2k2)=−m2g22k
Step 5: Using the Work-Energy Principle
According to the work-energy principle, the total work done on the block is equal to the change in kinetic energy. Since the block comes to rest, the change in kinetic energy is zero:
Wg+Ws+Wf=0
Where Wf is the work done by the external agent. Rearranging gives:
Wf=−(Wg+Ws)
Step 6: Substituting the Values
Substituting the expressions for Wg and Ws:
Wf=−(m2g2k−m2g22k)=−(m2g22k)=m2g22k
Final Answer
Thus, the work done by the external agent in lowering the block is:
Wf=m2g22k
When the block is lowered slowly, the forces acting on it are:
- The gravitational force Fg=mg acting downward.
- The spring force Fs=kx acting upward, where x is the compression of the spring.
Since the block is lowered slowly, it moves with zero acceleration. Therefore, the net force acting on the block is zero:
Fg−Fs=0⟹mg−kx=0
From this, we can express the compression of the spring x in terms of m and k:
kx=mg⟹x=mgk
The work done by gravity when the block is lowered by a distance x is given by:
Wg=mgh
Substituting h with x:
Wg=mgx=mg(mgk)=m2g2k
The work done by the spring when it is compressed by a distance x is given by:
Ws=−12kx2
Substituting x:
Ws=−12k(mgk)2=−12k(m2g2k2)=−m2g22k
According to the work-energy principle, the total work done on the block is equal to the change in kinetic energy. Since the block comes to rest, the change in kinetic energy is zero:
Wg+Ws+Wf=0
Where Wf is the work done by the external agent. Rearranging gives:
Wf=−(Wg+Ws)
Substituting the expressions for Wg and Ws:
Wf=−(m2g2k−m2g22k)=−(m2g22k)=m2g22k
Thus, the work done by the external agent in lowering the block is:
Wf=m2g22k
Similar Questions
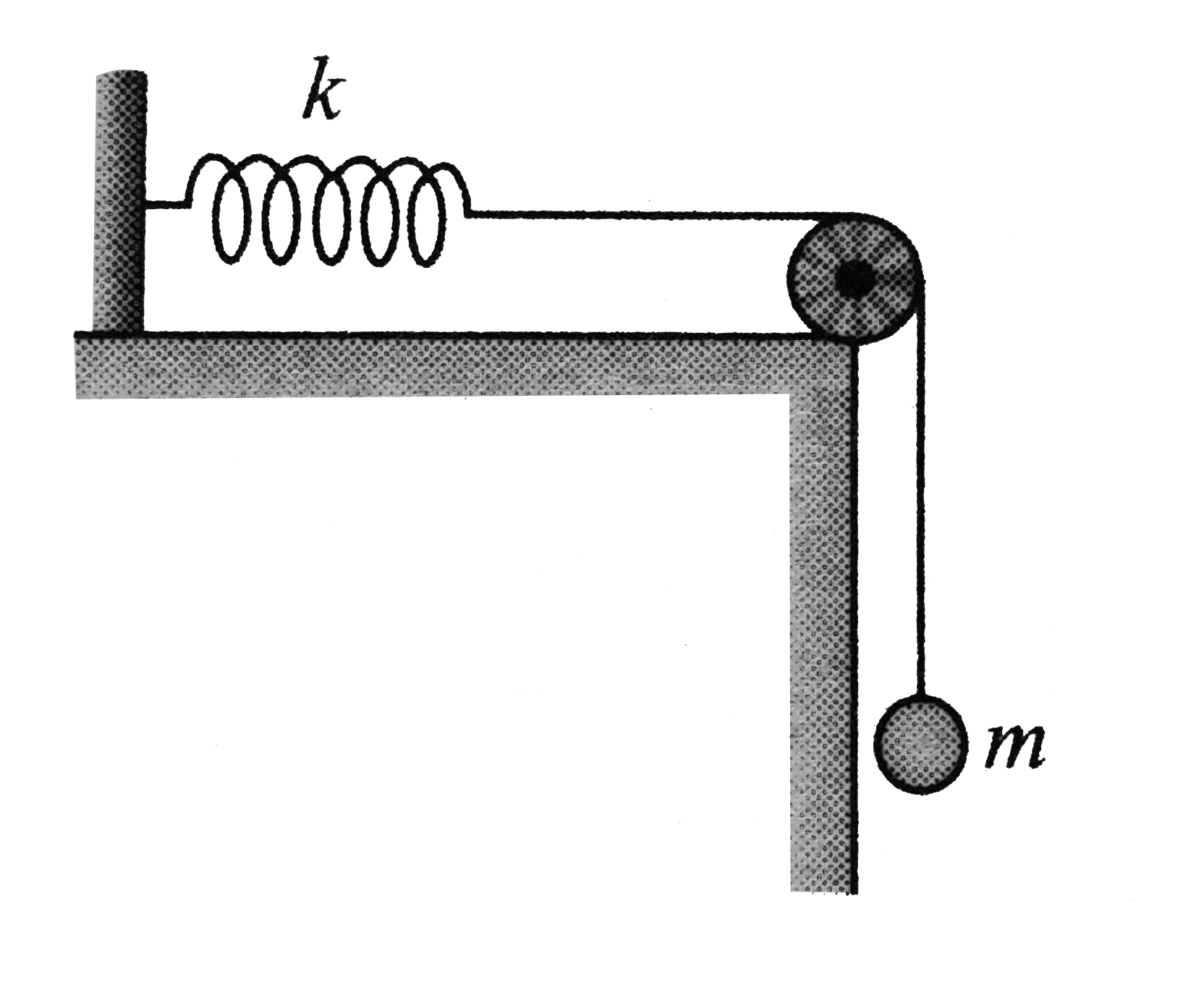
In figure, the light spring is of force constant k and is on a smooth horizontal surface. Initially the spring is relaxed. Calculate the work done by an external agent to lower the hanging body of mass M slowly, till it remains in equilibrium.
View SolutionWhat will be the work done by external agent to slowly hang the lower end of the chain to the peg?
View SolutionA block of mass m is slowly lowered from a point where it just touches a vertical fixed spring of stiffness k, till it remains stationary after the applied force is withdrawn. Find the work done by the external agent(a) in compressing the spring by a distance x and (b) bringing the block to its stable equilibrium position.

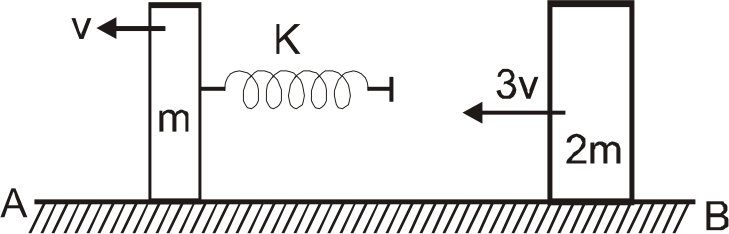
View SolutionAB is a long frictionless horizontal surface. One end of an ideal spring of spring constant K is attached to a block of mass m, which is being moved left with constant velocity v, and the another end is free. Another block of mass 2m is given a velocity 3v towards the spring. Magnitude of work done by external agent in moving m with constant velocity v in long time is β times mv2 . Find the value of β
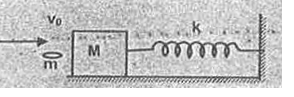
View SolutionA bullet of mass m strikes a block of mass M connected to a light spring of stiffness k, with a speed v0 and gets into it. Find the loss of K.E. of the bullet.
View SolutionIn the figure shown, a block A of mass m is rigidy attached to a light spring of stiffness k and suspended from a fixed support. Another block B of same mass is just placed on it and blocks are in equilibrium. Suddenly the block B is removed. Choose the correct options (s) afterward.
View SolutionA block Q of mass 2m is placed on a horizontal frictionless plane. A second block of mass m is placed on it and is connected to a spring of spring constant K, the two block are pulled by distance A. Block Q oscillates without slipping. The work done by the friction force on block Q when the spring regains its natural length is:
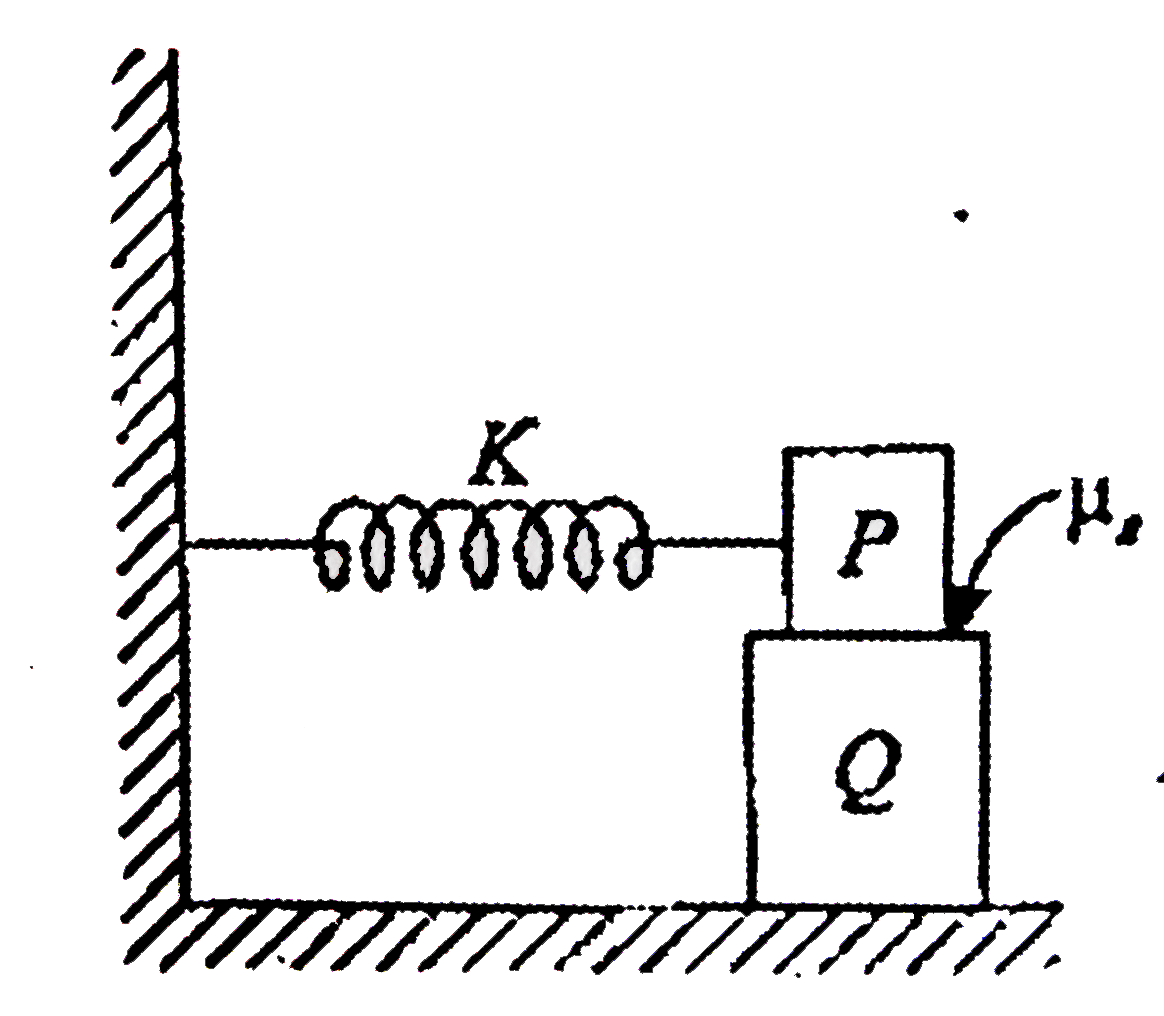
View SolutionIn the shown figure mass of the pulley is m and radius 2R. A light concentric spool of radius R is rigidly attached with the pulley. Two blocks A and B having masses m & 4m respectively are attached with the pulley by means of light strings. Lower surface of the block B is attached to a spring of stiffness ka and block B rests on a smooth inclined plane inclined 30∘ with horizontal. Other end of the spring is fixed to the ground. The block A is stretched a small distance and released then find the frequency of the oscillation of block B. (The strings do not slip on the pulley).

View SolutionFind out potential at P and Q due to the two point mass system Find out work done by external agent in bringing unit mass from P to Q Also find work done by gravitational force.
 .
.
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View Solution