A capacitor of capacitance C is connected to a cell of emf V and when fully charged, it is disconnected. Now the separation between the plates is doubled. The change in flux of electric field through a closed surface enclosing the capacitor is
Zero
To solve the problem step by step, we will analyze the situation involving a capacitor, its capacitance, and the electric field.
Step 1: Understand the Initial Conditions
- A capacitor of capacitance C is connected to a cell with an electromotive force (emf) V.
- When fully charged, the charge Q on the capacitor can be calculated using the formula:
Q=C⋅V
Hint: Remember that the charge on the capacitor is determined by its capacitance and the voltage applied across it.
Step 2: Disconnect the Capacitor
- After the capacitor is fully charged, it is disconnected from the cell. The charge Q remains on the plates of the capacitor.
Hint: Once the capacitor is disconnected, the charge does not change unless there is a path for it to discharge.
Step 3: Change in Plate Separation
- The problem states that the separation between the plates of the capacitor is doubled. Initially, the separation is D. After doubling, the new separation becomes 2D.
Hint: Doubling the separation affects the capacitance of the capacitor.
Step 4: Calculate the New Capacitance
- The capacitance of a parallel-plate capacitor is given by:
C=ϵ0AD
- After doubling the distance, the new capacitance C′ becomes:
C′=ϵ0A2D=C2
Hint: Capacitance is inversely proportional to the distance between the plates.
Step 5: Analyze the Electric Field
- The electric field E between the plates of a capacitor is given by:
E=VD
- When the separation is doubled, the voltage across the plates remains the same (since the charge is constant), but the new electric field E′ becomes:
E′=V2D=E2
Hint: The electric field strength decreases when the distance between the plates increases, assuming constant charge.
Step 6: Calculate the Electric Flux
- The electric flux Φ through a surface enclosing the capacitor is given by:
Φ=Qϵ0
- Since the charge Q remains constant (as the capacitor is isolated), the electric flux before and after the separation change remains the same.
Hint: Electric flux depends on the total charge enclosed and does not change unless the charge itself changes.
Step 7: Determine the Change in Flux
- Since the charge enclosed by the closed surface around the capacitor does not change, the change in electric flux ΔΦ is:
ΔΦ=Φ′−Φ=0
Hint: If the charge enclosed remains constant, the change in electric flux is zero.
Conclusion
The change in flux of the electric field through a closed surface enclosing the capacitor is zero.
Final Answer: The change in flux is 0.
- A capacitor of capacitance C is connected to a cell with an electromotive force (emf) V.
- When fully charged, the charge Q on the capacitor can be calculated using the formula:
Q=C⋅V
- After the capacitor is fully charged, it is disconnected from the cell. The charge Q remains on the plates of the capacitor.
- The problem states that the separation between the plates of the capacitor is doubled. Initially, the separation is D. After doubling, the new separation becomes 2D.
- The capacitance of a parallel-plate capacitor is given by:
C=ϵ0AD
- After doubling the distance, the new capacitance C′ becomes:
C′=ϵ0A2D=C2
- The electric field E between the plates of a capacitor is given by:
E=VD
- When the separation is doubled, the voltage across the plates remains the same (since the charge is constant), but the new electric field E′ becomes:
E′=V2D=E2
- The electric flux Φ through a surface enclosing the capacitor is given by:
Φ=Qϵ0
- Since the charge Q remains constant (as the capacitor is isolated), the electric flux before and after the separation change remains the same.
- Since the charge enclosed by the closed surface around the capacitor does not change, the change in electric flux ΔΦ is:
ΔΦ=Φ′−Φ=0
The change in flux of the electric field through a closed surface enclosing the capacitor is zero.
Similar Questions
A capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the capacitor is
View SolutionA parallel plate capacitor of capacitance 10μF is connected to a cell of emf 10 V and is fully charged. Now a dielectric slab (k = 3) of thickness equal to the gap between the plates is completely filled in the gap, keeping the cell connected. During the filling process,
View Solution
Knowledge Check
A parallel plate capacitor without any dielectric within its plates, has a capacitance C, and is connected to a battery of emf V. The battery is disconnected and the plates of the capacitor are pulled apart until the separation between the plates is doubled. What is the work done by the agent pulling the plates apart, in this process ?
A12CV2B32CV2C−32CV2DCV2
A capacitor of capacitance C carrying charge Q is connected to a source of emf E. Finally, the charge on capacitor would be
View SolutionAnswer the following:
(a) When a parallel plate capacitor is connected across a dc battery, explain briefly how the capacitor gets charged.
(b) A parallel plate capacitor of capacitance 'C' is charged to 'V' volt by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant 1<k<2 is introduced to fill the space between the plates. How will the following be affected ?
(i) The electric field between the plates of the capacitor.
(ii) The energy stored in the capacitor. Justify your answer in each case.
(c) The electric potential as a function of distance 'x' is shown in the figure. Draw a graph of the electric field E as a function of x.
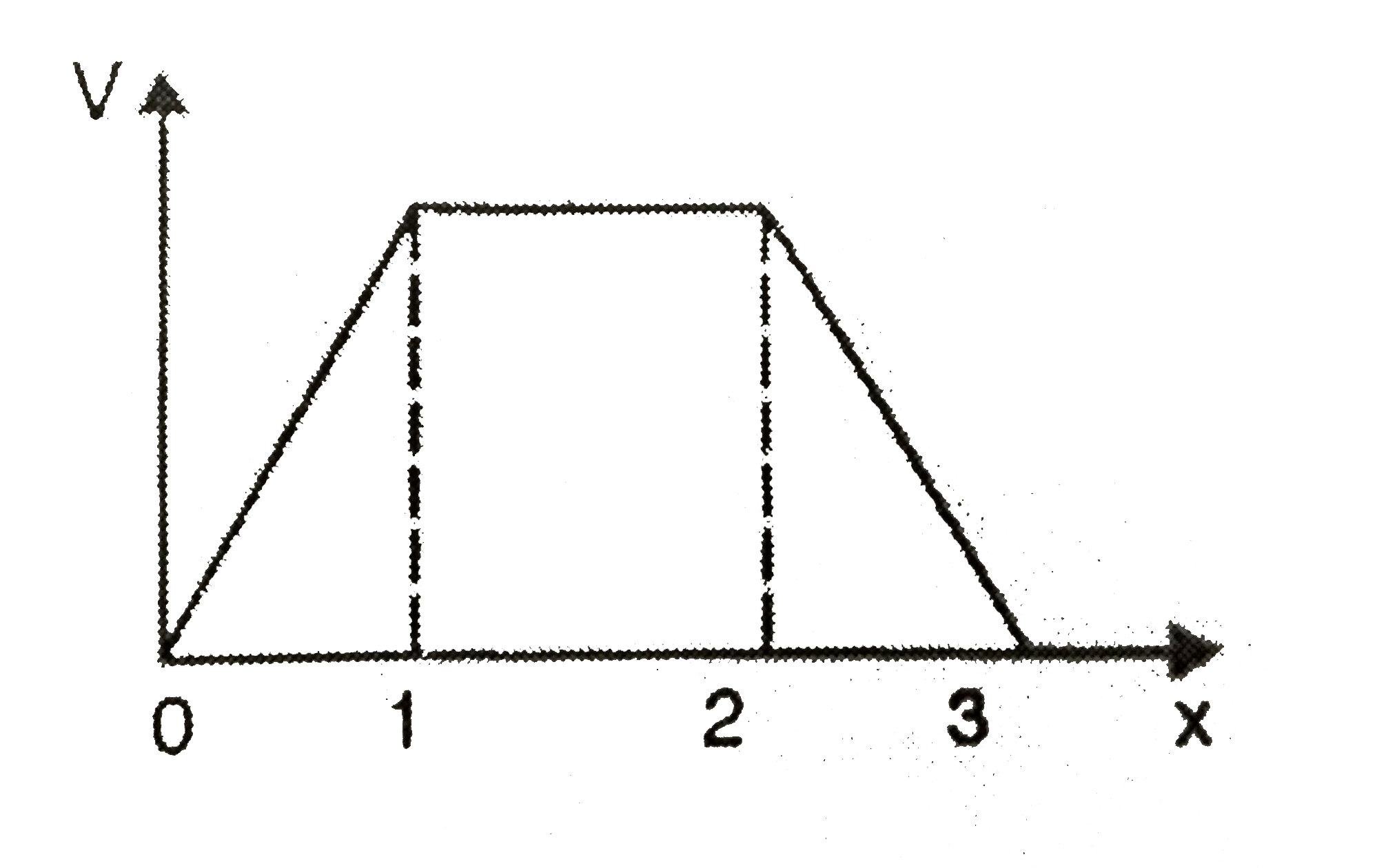
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
View SolutionA parallel plate capacitor is charged from a cell and then isolated from it. The separation between the plates is now increased
View SolutionA parallel plate capacitor is charged from a cell and then isolated from it. The separation between the plates is now increased
View SolutionA parallel plate capacitor is connected to a battery. The plates are pulled apart with uniform speed. If x is the separation between the plates, then the rate of change of electrostatic energy of the capacitor is proportional to
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V by a battery. Without disconnecting the battery, distance between the plates of capacitor is tripled and a dielectric medium of K = 10 is introduced between the plates of capacitor. Explain giving reasons how will the following be affected ?
(a) Capacitance of capacitor
(b) Charge on capacitor
(c ) Energy density of capacitor.
View Solution