A parallel plate capacitor is connected to a battery. The plates are pulled apart with uniform speed. If x is the separation between the plates, then the rate of change of electrostatic energy of the capacitor is proportional to
x2
x
1x
1x2
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the electrostatic energy of a parallel plate capacitor and the separation between its plates. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Capacitance of a Parallel Plate Capacitor
The capacitance C of a parallel plate capacitor is given by the formula:
C=ε0Ax
where:
- ε0 is the permittivity of free space,
- A is the area of one of the plates,
- x is the separation between the plates.
Step 2: Energy Stored in the Capacitor
The energy U stored in a capacitor is given by:
U=12CV2
Since the capacitor is connected to a battery, the voltage V remains constant. Substituting the expression for capacitance into the energy formula gives:
U=12(ε0Ax)V2=12ε0AV2x
Step 3: Differentiate the Energy with Respect to Time
To find the rate of change of energy dUdt, we differentiate U with respect to time t:
dUdt=ddt(12ε0AV2x)
Using the quotient rule for differentiation, we get:
dUdt=−12ε0AV2x2dxdt
where dxdt is the rate at which the plates are being pulled apart.
Step 4: Analyze the Proportionality
From the expression derived, we see that:
dUdt∝−1x2dxdt
This indicates that the rate of change of electrostatic energy dUdt is inversely proportional to the square of the separation x.
Conclusion
Thus, the rate of change of electrostatic energy of the capacitor is proportional to 1x2.
Final Answer
The rate of change of electrostatic energy of the capacitor is proportional to 1x2.
---
The capacitance C of a parallel plate capacitor is given by the formula:
C=ε0Ax
where:
- ε0 is the permittivity of free space,
- A is the area of one of the plates,
- x is the separation between the plates.
The energy U stored in a capacitor is given by:
U=12CV2
Since the capacitor is connected to a battery, the voltage V remains constant. Substituting the expression for capacitance into the energy formula gives:
U=12(ε0Ax)V2=12ε0AV2x
To find the rate of change of energy dUdt, we differentiate U with respect to time t:
dUdt=ddt(12ε0AV2x)
Using the quotient rule for differentiation, we get:
dUdt=−12ε0AV2x2dxdt
where dxdt is the rate at which the plates are being pulled apart.
From the expression derived, we see that:
dUdt∝−1x2dxdt
This indicates that the rate of change of electrostatic energy dUdt is inversely proportional to the square of the separation x.
Thus, the rate of change of electrostatic energy of the capacitor is proportional to 1x2.
The rate of change of electrostatic energy of the capacitor is proportional to 1x2.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
A parallel plate capacitor is charged. If the plates are pulled apart
View SolutionA capacitor is connected to a battery. The force of attraction between the plates when the separation between them is halved.
View SolutionA parallel plate capacitor is connected across a battery. Now, keeping the battery connected, a dielectric slab is inserted between the plates. In the process,
View SolutionA parallel-plate capacitor is connected to a battery. A metal sheet of negligible thickness is placed between the plates. The sheet remains parallel to the plates of the capacitor.
View SolutionA parallel plate capacitor is charged and then isolated. On increasing the plate separation
View SolutionA parallel plate capacitor has capacitance of 1.0F. If the plates are 1.0mm apart, what is the area of the plates?
View SolutionA parallel plate air capacitor is connected to a battery. If the plates of the capacitor are pulled farther apart, then state whether the following statements are true or false.
a. Strength of the electric field inside the capacitor remains unchanged, if the battery is disconnected before pulling the plates.
b. During the process, work is done by the external force applied to pull the plates irrespective of whether the battery is disconnected or not.
c. Strain energy in the capacitor decreases if the battery remains connected.
 .
.
View SolutionIf the separation between the plates of a capacitor is 5 mm , then area of the plate of a 3 F parallel plate capacitor is
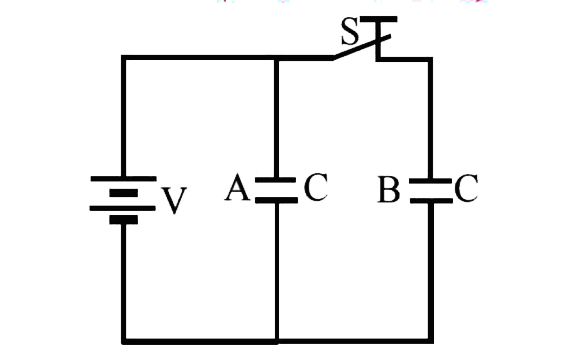
View SolutionThe figure shows two identical parallel plate capacitors connected to a battery with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant(or relative permittivity) 3. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
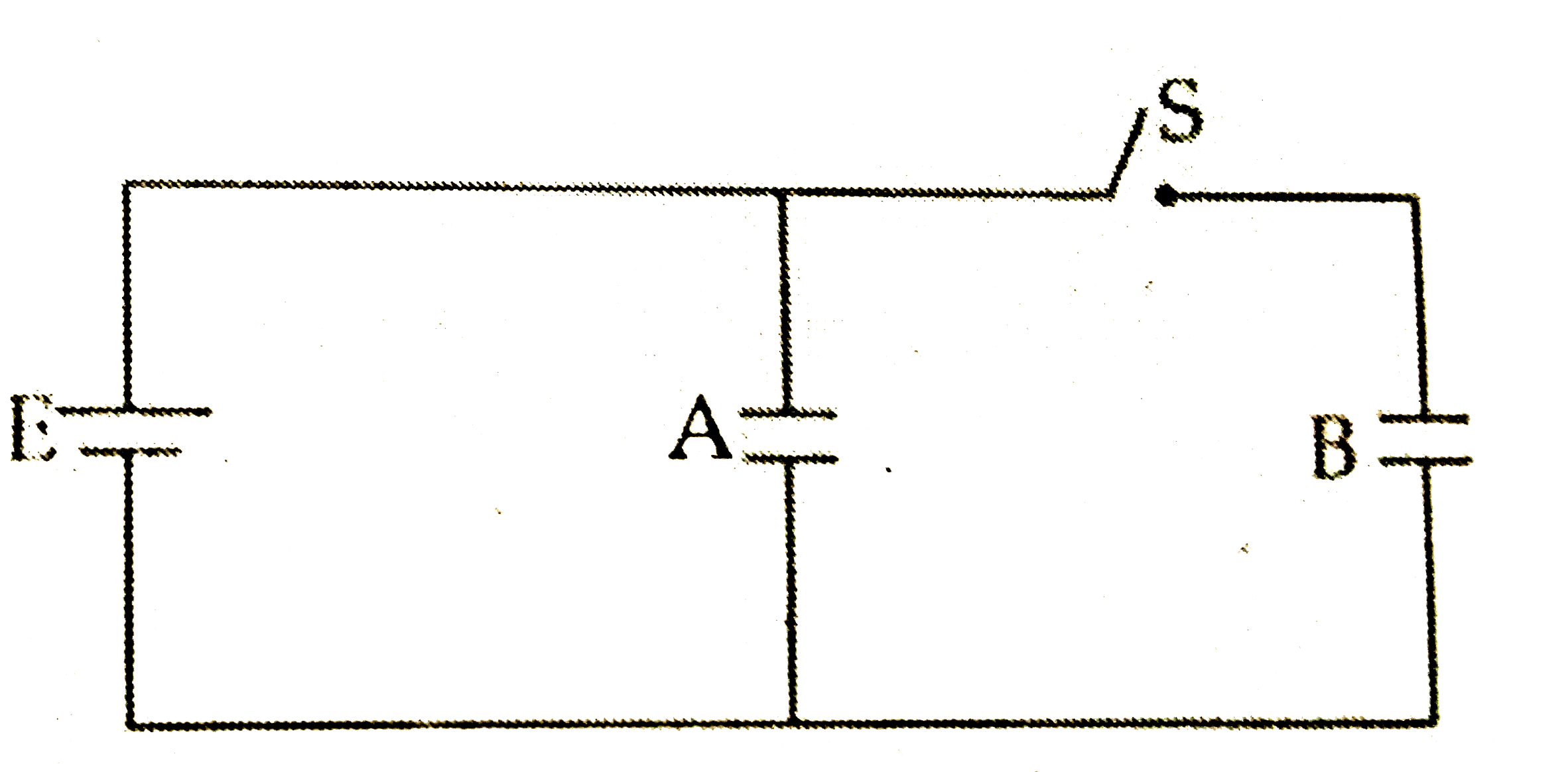
View SolutionTwo identical parallel plate capacitors A and B are
connected to a battery of V volts with the switch S
closed . The switch is now opend and the free
space between the plantes of the capacitors is filled
with a dielectric of dielectric constant K. Find the
rario of the total electrostatic energy stored in both
capacitors before and after the introduction of the dielectric.
View Solution
