In Young's double slit experiment, the fringes are displaced index 1.5 is introduced in the path of one of the beams. When this plate in replaced by another plate of the same thickness, the shift of fringes is (3/2)x. The refractive index of the second plate is
1.75
1.50
1.25
1.00
The path difference introduced by a plate of thickness t and refractive index μ is given by
Δ=(μ−1)t
A path difference of λ introduced a phase shift of β where ϕ=λD/(2d).2d= separation between slits
So, a path difference of (μ−1)t introduces a shift x on the screen given by
x=(μ−1)tβλ
for first plate, x=(μ1−1)tβλ
for second plate 32x=(μ2−1)tβλ
∴(μ2−1)(μ1−1)=32⇒(μ2−1)(1.5−1)=32
⇒μ2=1.75
Similar Questions
In a Young.s double slit experiment, the fringes are displaced by a distance x when a glass plate of refractive index 1.5 is introduced in the path of one of the beams. When this plate is replaced by another plate of same thickness, the shift of fringes is (3/2)x. The refractive index of second plate is
View SolutionIn a young 's double slit experiment, a glass plate of refractive index 1.5 and thickness 5×10−4 cm is kept in the path of one of the light rays. Then
View Solution
Knowledge Check
Interference fringes were produced in Young's double slit experiment using light of wavelength 5000 Ã…. When a film of material 2.5×10−3cm thick was placed over one of the slits, the fringe pattern shifted by a distance equal to 20 fringe widths. The refractive index of the material of the film is
A1.25B1.33C1.4D1.5
In Young's double slit experiment a mica plate of refractive index μ is introduced in the path of light coming from one of the slit . If the central bright fringe gets shifted to the point originally occupied by the fourth bright fringe, then the thickness of the mica plate will be (symbols have their usual meaning )
View SolutionWhen a thin transparent plate of Refractive Index 1.5 is introduced in one of the interfearing becomes, 20 fringes shift. If it is replaced by another thin plate of half the thickness and of R.I 1.7 the number of fringes that undergo displacement is
View SolutionWhen a mica plate of thickness 0.1mm is introduced in one of the interfering beams, the central fringe is displaced by a distance equal to 10 fringes. If the wavelength of the light is 6000A0, the refractive index of the mica is
View SolutionIn Young's experiment the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index 1.7 interference pattern is observed using light of wavelength 5400Å
It is found that point P on the screen where the central maximum (n=0) fell before the glass plates were inserted now has 3/4 the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P.
Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected.
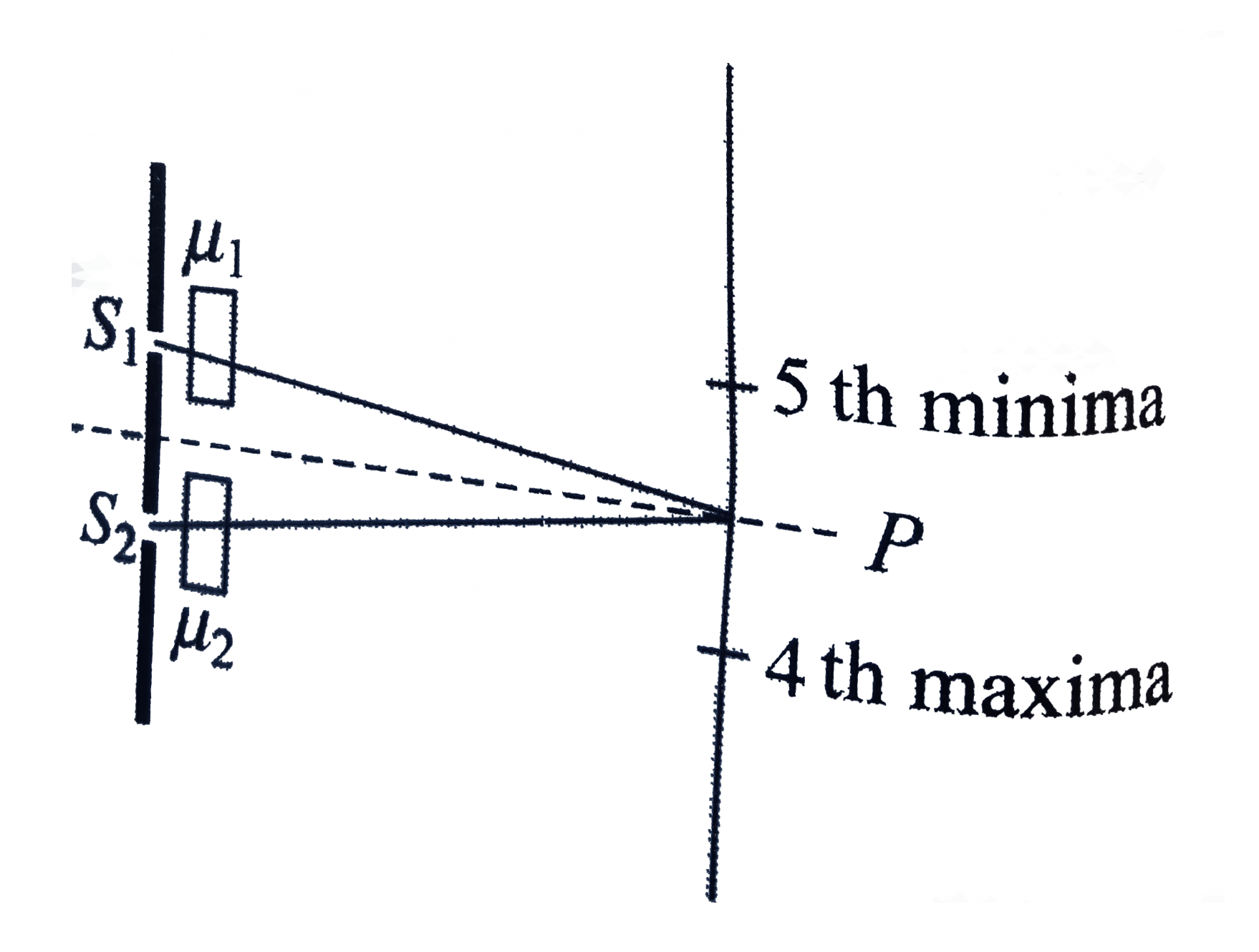 .
.
View SolutionIn young's double slit experiment the fringe width is 4mm. If the experiment is shifted to water of refractive index 4/3 the fringe width becomes (in mm)
View SolutionIn Young's double slit experiment a mica sheet of thickness t and refractive index μ is introduced in the path of ray from the first source S1 By how much distance thhe fringe pattern will be displaced.
View SolutionLight of wavelength 500nm is used to form interference pattern in Young's double slit experiment. A uniform glass plate of refractive index 1.5 and thickness 0.1mm is introduced in the path of one of the interfering beams. The number of fringes which will shift the cross wire due to this is
View Solution
