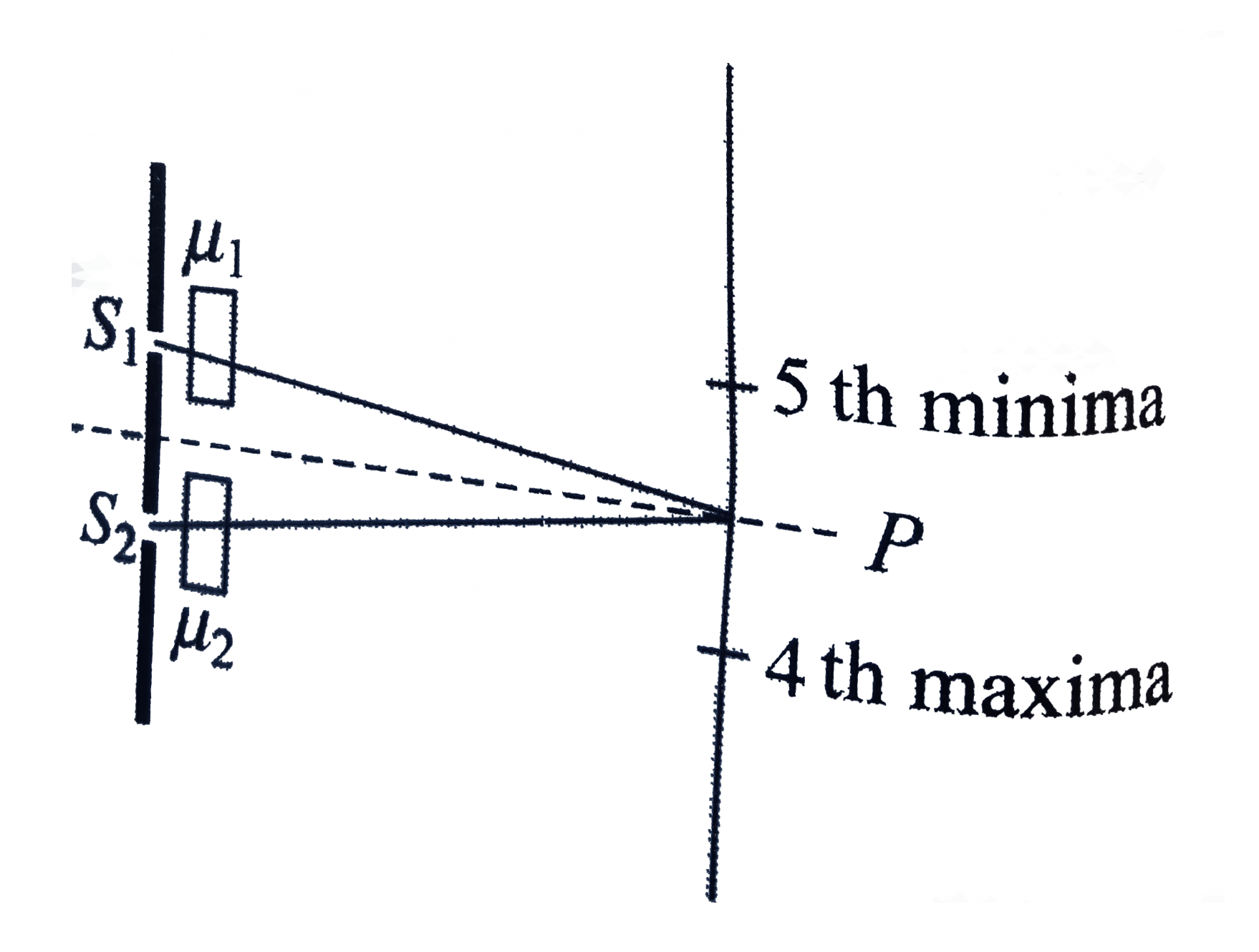
In Young's experiment the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index 1.7 interference pattern is observed using light of wavelength 5400Å
It is found that point P on the screen where the central maximum (n=0) fell before the glass plates were inserted now has 3/4 the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P.
Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected.
 .
.
At point P (central maxima), originally it has maximum intensity. If the intensity coming out of each slit is I0, the intensity at point P should be 4I0.
I=2I0(1+cosϕ)⇒34(4I0)=2I0(1+cosϕ)
cosϕ=12⇒ϕ=2nπ±π3 (n is integer)
Path difference at P,
4λ≤Δx≤(2×5−12)λ
⇒4λ≤Δx≤92λ⇒4λ≤Δx≤4.5λ
From Eq. (i),
θ=2πλΔx⇒Δx=nλ±λ6
Δx=λ(4±16)
From Eqs. (ii) and (iii), n=4. Hence,
Δxλ(4+16)=256λ⇒Δx=t(μ−1)
t=25λ6(μ2−μ1)=25×5400×106×0.3×10−1=7500×10−9m
=7.5μm
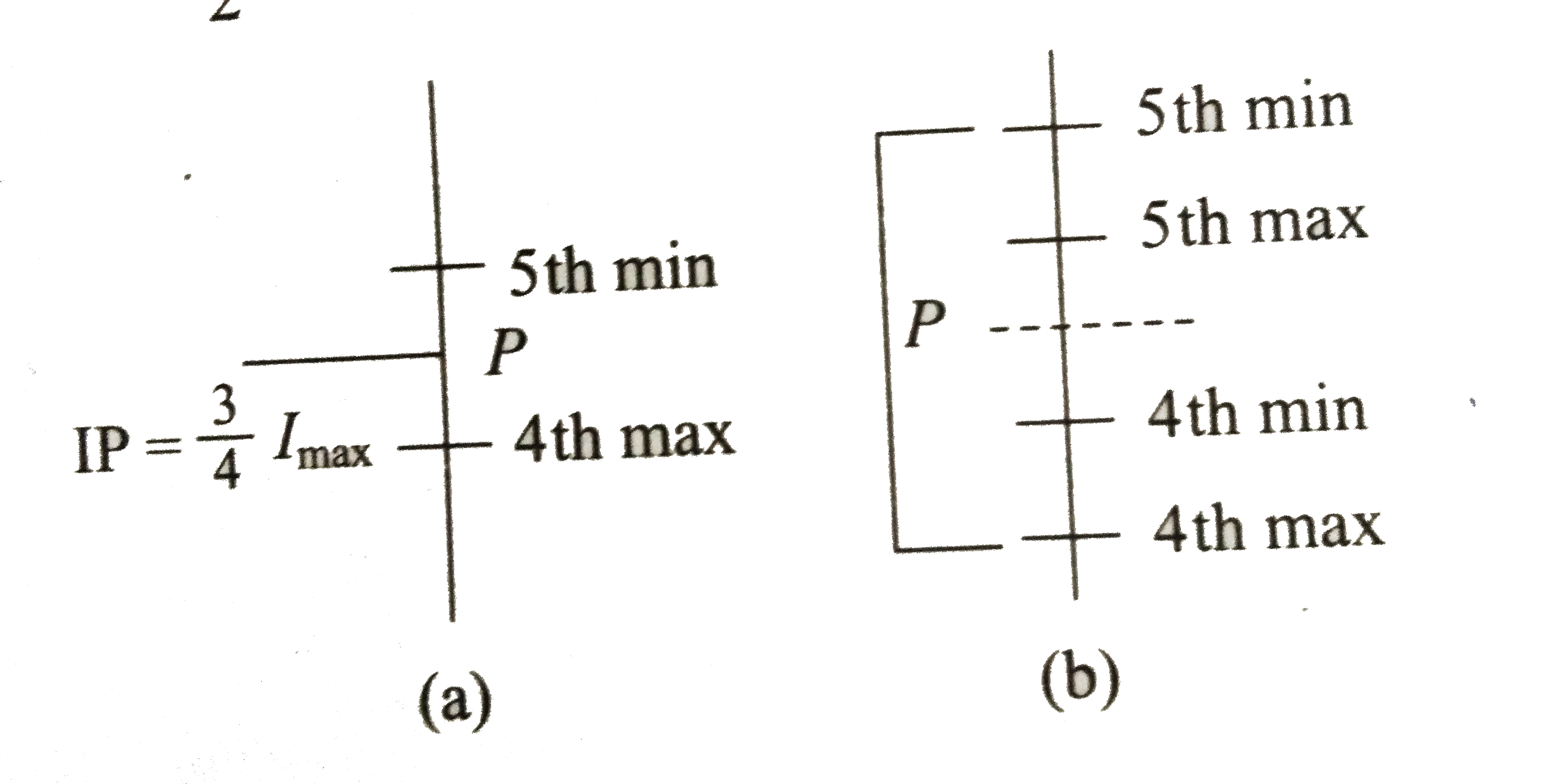
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Solved Examples
10 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.1
12 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
In Young's double slit experiment, the fringes are displaced index 1.5 is introduced in the path of one of the beams. When this plate in replaced by another plate of the same thickness, the shift of fringes is (3/2)x. The refractive index of the second plate is
View SolutionIn Young's experiment one slit is covered with a blue filter and the other (slit) with a yellow filter then the interference pattern
View SolutionIn a Young.s double slit experiment, the fringes are displaced by a distance x when a glass plate of refractive index 1.5 is introduced in the path of one of the beams. When this plate is replaced by another plate of same thickness, the shift of fringes is (3/2)x. The refractive index of second plate is
View SolutionThe central fringe shifts to the position of fifth bright fringe, if a thin film of refractive index 1.5 is introduced in the path of light of wavelength 5000Å. The thickness of the glass plate is
View SolutionRefractive index of a thin soap film of a uniform thickness is 1.34. Find the smallest thickness of the film that gives in interference maximum in the reflected light when light of wavelength 5360Å fall at normal incidence.
View SolutionIn a double-slit experiment, fringes are produced using light of wavelength 4800A∘. One slit is covered by a thin plate of glass of refractive index 1.4 and the other slit by another plate of glass of double thickness and of refractive index 1.7. On doing so, the central bright fringe shifts to a position originally occupied by the fifth bright fringe from the center. find the thickness of the glass plates.
View SolutionLight of wavelength 6000Å is incident on a thin glass plate of refractive index 1.5 such that angle of refraction into the plate is 60∘. Calculate the smallest thickness of plate which will make it appear dark by reflection.
View SolutionIn a young 's double slit experiment, a glass plate of refractive index 1.5 and thickness 5×10−4 cm is kept in the path of one of the light rays. Then
View SolutionLight of wavelength 3000A is incident on a thin glass plate of refractive index 1.5 such that angle of refraction into plate is 60° .calculate the thickness of plate which will make it appear dark by reflection?
View SolutionLight of wavelength 3000A is incident on a thin glass plate of refractive index1 such that angle of refraction into plate is 60° .calculate the thickness of plate which will make it appear dark by reflection?
View Solution
