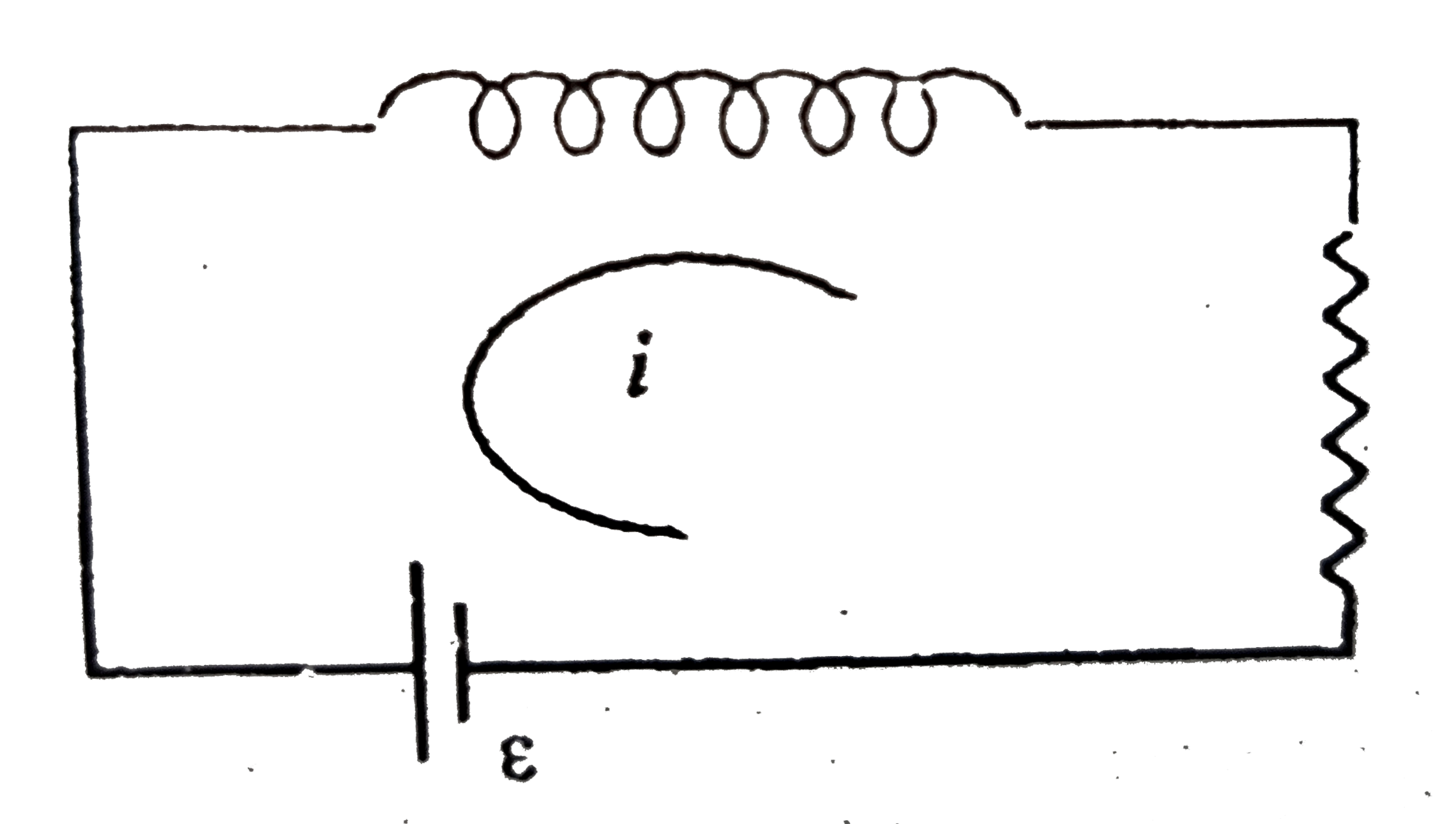
An iron core solenoid of length l and cross-sectional area A having N turns on it is connected to a battery through a resistance as shown in the figure. At instant t=0, the iron rod of permeability μ from the core is abruptly removed. Find the current as a function of time.

Self inductance of the solenoid
L=μ0μN2Al
and initial current i0=εR because circuit is in the steady state.
When iron rod is abruptly removed from the core the number of flux linkages abruptly do no change.
Nϕ=Li0=L'i0'
(μ0μN2Al)i0=(μ0N2Al)i'0
∴ Just after t=0, initial current i0'=μi0=μ(εR)
At instant, if the current in the circuit is i, then apply KVL in the loop, we get
Ldidt+iR=ε
−Ldi(ε−iR)=dt
On integration we get,
L−Rln(ε−iR)=t+c1
At t=0, i=i0'=(μεR)
⇒(L−R)ln(ε−i0'R)=C1
∴ln(ε−iRε−i0'R)=−tRL⇒(ε−iRε−i0'R)=e−tRL
⇒⎛⎜
⎜⎝ε−iRε−(μεR)R⎞⎟
⎟⎠=e−tRL
On rearraging the equation, we get
i=εR[1+(μ−1)e−tR/L]
Similar Questions
The self inductance of a solenoid of length L, area of cross-section A and having N turns is-
View SolutionAn air cored solenoid of length 50 cm and area of cross section 28m2 has 200 turns and carries a current of 5.0 A. On switching off, the current decreases to across the ends of the solenoid. Find flux and emf induced if time is equal to 1.0 ms.
View Solution
Knowledge Check
A solenoid is connected to a battery so that a steady current flows through it. If an iron core is inserted into the solenoid, then
AincreaseBdecreaseCremains sameDfirst increase then decrease
Current I flows through solenoid of length L having N number of turns, when it is connected to DC emf. If charged particle is projected along the axis of solenoid with a speed v0, them find the force on the charged particle in the solenoid.
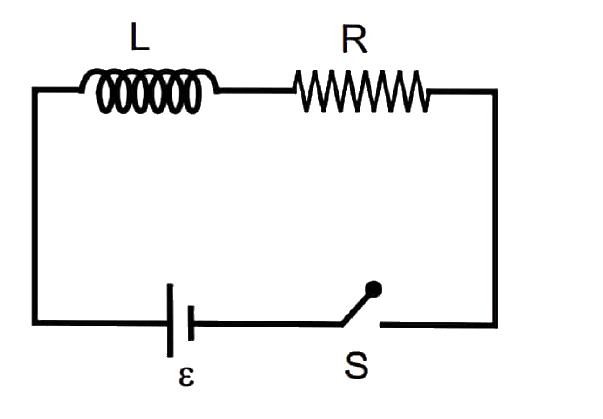
View SolutionThe figure below shows a battery of emf ε connected to an inductor L and resistance R in series. If the switch is closed at t=0, then the total charge that flows from the battery in time constant of the circuit is
View SolutionA solenoid having an iron core has its terminals connected across an ideal DC source and it is in steady state.If the iron core is removed the current flowing through the solenoid just after removal of rod

View SolutionA solenoid of resistance R and inductance L has a piece of soft iron inside it. A battery of emf E and of negligible internal resistance is connected across the solenoid as shown in Fig. At any instant, the piece of soft iron is pulled out suddenly so that inductance of the solenoid decrease to ηL(η<1) with battery remaining connected.
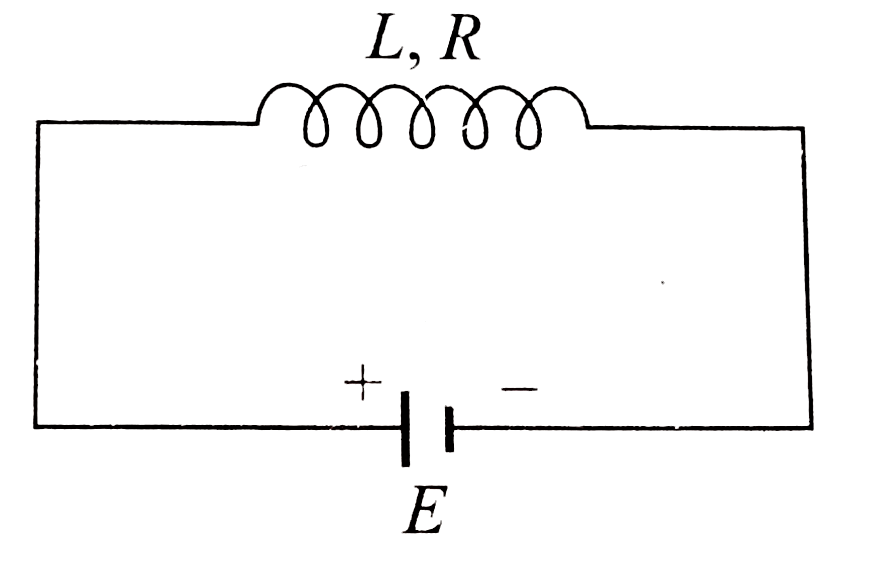
Assume t = 0 is the instant when iron piece has been pulled out, the current as a function of time after this is
View SolutionTwo insulated wires are wound on the same hollow cylinder, s as to from two solenoids shering a common air-filled core. Let l be the length of the core, A the cross -sectional area of the core, N1 the number of times the first wire is wound around the core, and N2 the number of times the second wire is wound around the core. Find the mutual inductance of the two solenoids, neglecting the end effects.
View SolutionTwo insulated wires are wound on the same hollow cylinder so as to form two solenoids sharing a common air-filled core. Let l be the length of the core, A the cross -sectional area of the core, N1 the number of times the first wire is wound around the core, and N2 the number of times the second wire is wound around the core. Find the mutual inductance of the two solenoids, neglecting the end effects.
View SolutionAn indcutor having self inductance L with its coil resistance R is connected across a battery of emf elipson. When the circuit is in steady state t = 0, an iron rod is inserted into the inductor due to which its inductance becomes nL (ngt1).
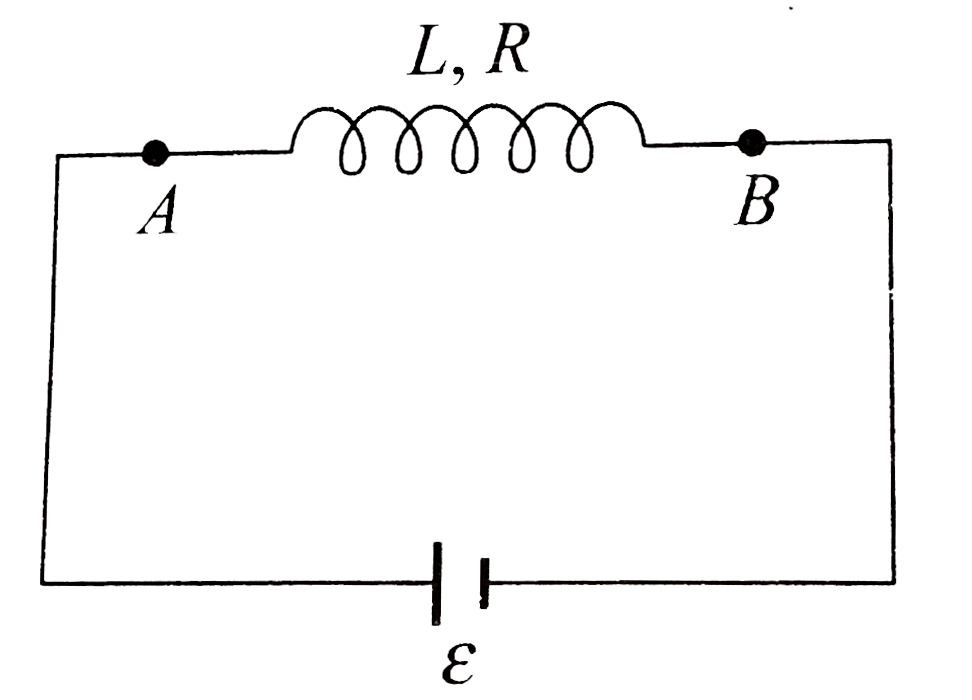
after insertion of rod, current in the circuit:
View Solution
