Two insulated wires are wound on the same hollow cylinder, s as to from two solenoids shering a common air-filled core. Let be the length of the core, A the cross -sectional area of the core, the number of times the first wire is wound around the core, and the number of times the second wire is wound around the core. Find the mutual inductance of the two solenoids, neglecting the end effects.
To find the mutual inductance M of the two solenoids sharing a common air-filled core, we can follow these steps:
Step 1: Understand the Magnetic Field Created by the First Solenoid
When a current I1 flows through the first solenoid (with N1 turns), it generates a magnetic field B1 in the core. The formula for the magnetic field inside a solenoid is given by:
B1=μ0N1I1l
where:
- μ0 is the permeability of free space,
- N1 is the number of turns in the first solenoid,
- I1 is the current flowing through the first solenoid,
- l is the length of the solenoid.
Step 2: Calculate the Magnetic Flux Linked with the Second Solenoid
The magnetic flux Φ1 linked with a single turn of the second solenoid (with N2 turns) is given by:
Φ1=B1⋅A
Substituting B1 from Step 1, we get:
Φ1=(μ0N1I1l)A
Step 3: Calculate the Total Flux Linked with the Second Solenoid
The total magnetic flux linked with all N2 turns of the second solenoid is:
Φtotal=N2Φ1=N2(μ0N1I1lA)
Step 4: Define the Mutual Inductance
The mutual inductance M is defined by the relationship between the total flux linked with the second solenoid and the current in the first solenoid:
Φtotal=MI1
From Step 3, we can equate this to find M:
MI1=N2(μ0N1I1lA)
Step 5: Solve for Mutual Inductance M
Dividing both sides by I1 (assuming I1≠0) gives:
M=μ0N1N2Al
Final Result
Thus, the mutual inductance of the two solenoids is:
M=μ0N1N2Al
---
When a current I1 flows through the first solenoid (with N1 turns), it generates a magnetic field B1 in the core. The formula for the magnetic field inside a solenoid is given by:
- μ0 is the permeability of free space,
- N1 is the number of turns in the first solenoid,
- I1 is the current flowing through the first solenoid,
- l is the length of the solenoid.
The magnetic flux Φ1 linked with a single turn of the second solenoid (with N2 turns) is given by:
The total magnetic flux linked with all N2 turns of the second solenoid is:
The mutual inductance M is defined by the relationship between the total flux linked with the second solenoid and the current in the first solenoid:
Dividing both sides by I1 (assuming I1≠0) gives:
Thus, the mutual inductance of the two solenoids is:
Topper's Solved these Questions
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Exercises (subjective)
Explore 7 Videos
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Exercises (single Correct )
Explore 65 Videos
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Solved Examples
Explore 3 Videos
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:HEATING EFFECT OF CURRENTExercise:Thermal Power in Resistance Connected in Circuit
Explore 27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Multiple Correct Answer type
Explore 2 Videos
Similar Questions
Two insulated wires are wound on the same hollow cylinder so as to form two solenoids sharing a common air-filled core. Let l be the length of the core, A the cross -sectional area of the core, N1 the number of times the first wire is wound around the core, and N2 the number of times the second wire is wound around the core. Find the mutual inductance of the two solenoids, neglecting the end effects.
View SolutionIn opticle fibres,the refractive index of the core is
View Solution
Knowledge Check
The self inductance of a solenoid that has a cross-sectional area of 1cm2, a length of 10 cm and 1000 turns of wire is
A0.86mHB1.06mHC1.26mHD1.46mH
A solenoidal coil has 50 turns per centimetre along its length and a cross-sectional area of 4×10−4m2. 200 turns of another wire is wound round the first solenoid co-axially. The two coils are electrically insulated from each other. Calculate the mutual inductance between the two coils.
View SolutionWhen a wire is wound around a soft iron bar, and a current is passed through it, the soft iron bar behaves like a magnet.
View Solution9 + 2 array of microtubules is found in the core of
View SolutionName two factors on which the self-inductance of an air-core coil depends.
View SolutionA toroid is wound over a circular core. Radius of each turn is r and radius of toroid is R(>>r). The coefficient of self-inductance of the toroid is given by
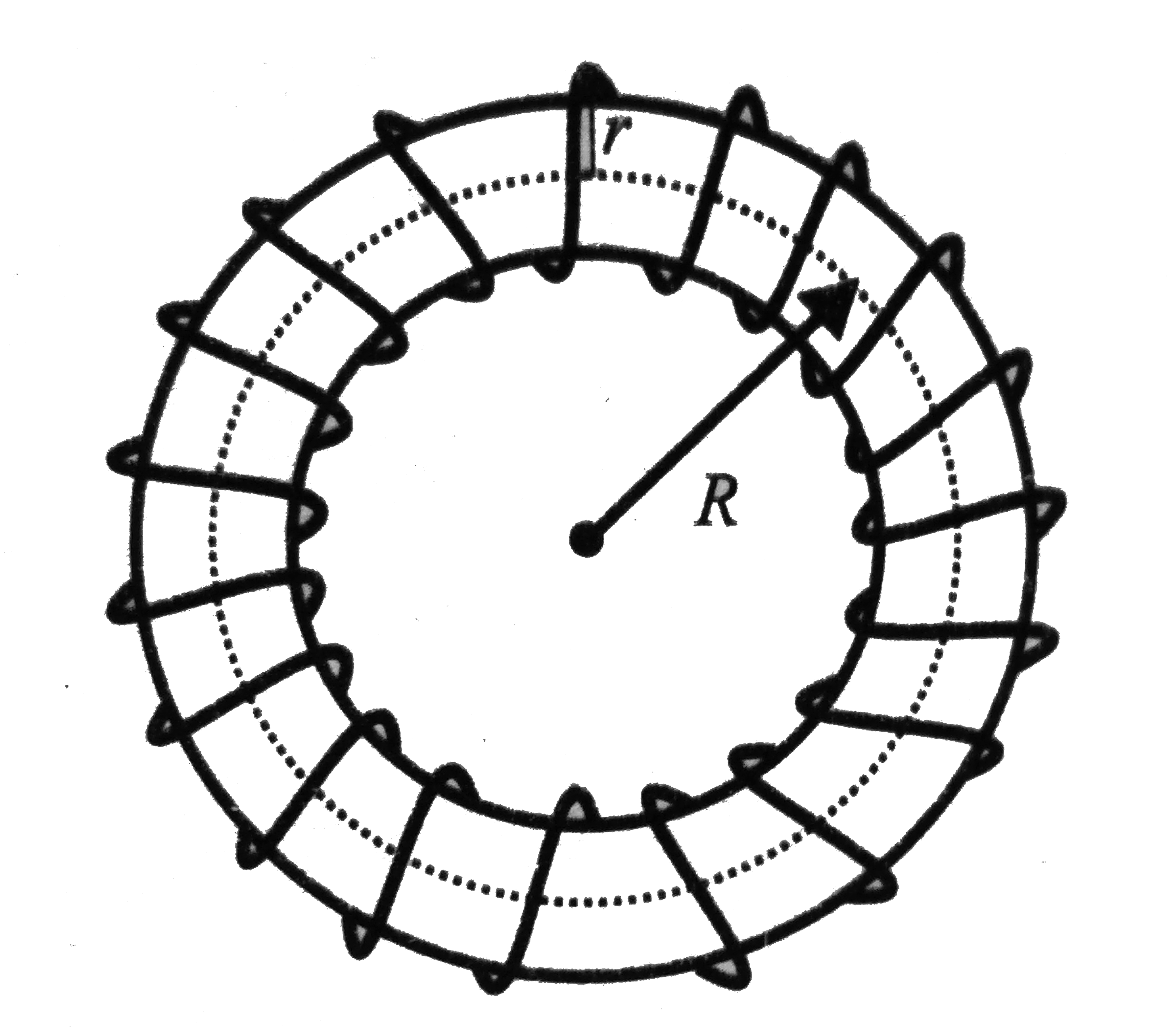
View SolutionThe core of the cilium (or) the flagellum is called
View SolutionIn an electromagnet, the core is made up of copper.
View Solution