If the current in the inner loop changes according to I=2t2 (Fig .), then find the current in the capacitor as a function of time.

M=μ02bπa2
|emf induced in larger coil|=[(didt) in smaller coil]
e=μ02bπa2(4t)=2μ0πa2tb
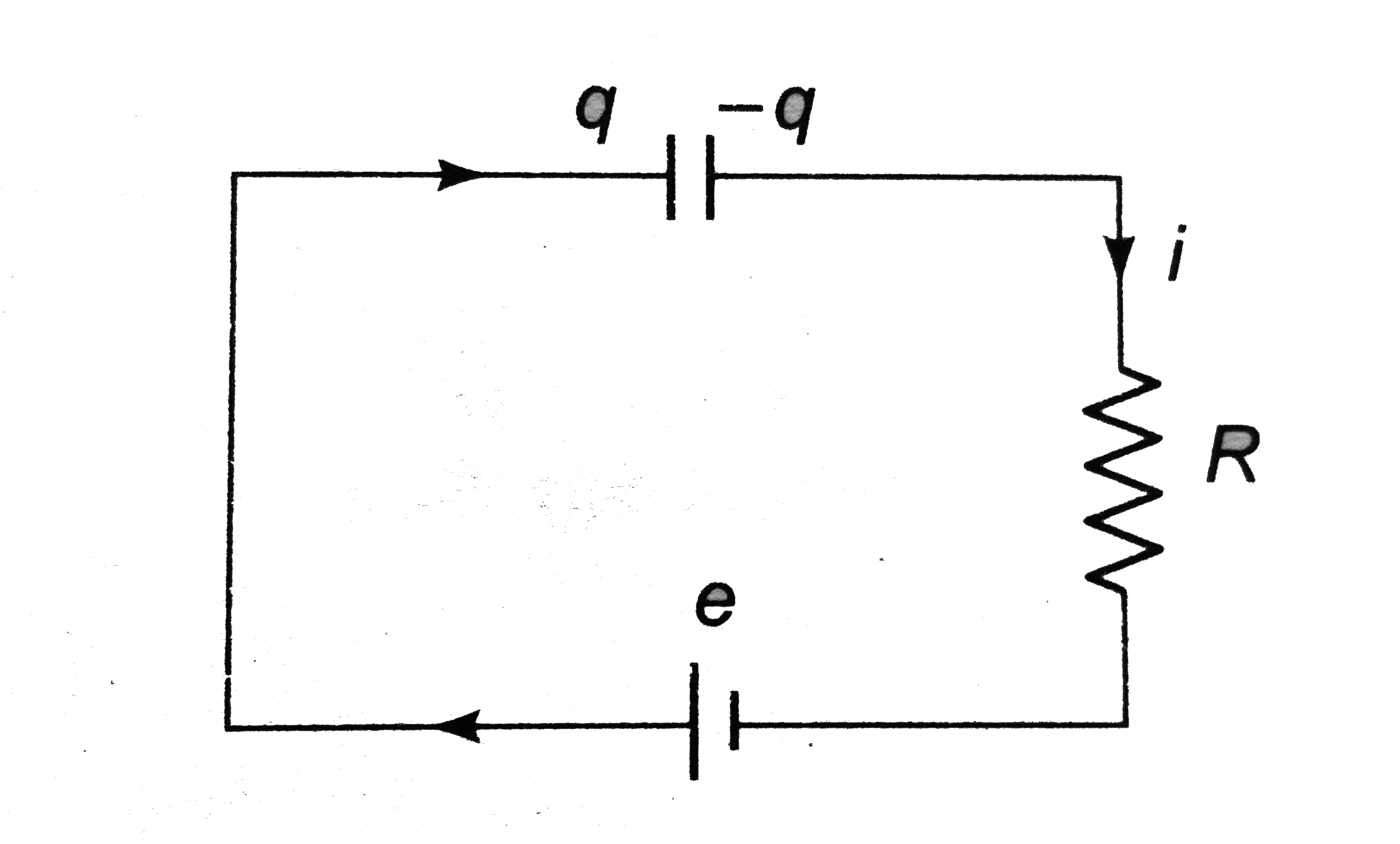
Applying KVL,
+e−qC−iR=0⇒2μ0πa2tb−qC−iR=0
Differentiating w.r.t. time, we get
2μ0πa2b−iC−didtR=0=0
On solving, i=2μ0πa2Cb[1−e−t/RC]
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (subjective)
7 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (single Correct )
65 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Solved Examples
3 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
If the current in the inner loop changes according to i=2t2 then, find the current in the capacitor as a function of time.

View SolutionFind the current in the loop
View SolutionFigure. shows two concentric coplanar coils with radii a and b(a<<b). A current I=2t flows in the smaller loop. Neglecting self-inductance of the larger loop, if a capacitor of capacitance C is also connected in the larger loop as shows in Fig . , find the charge on the capacitor as a function of time.

View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionFigure. shows two concentric coplanar coils with radii a and b(a<<b). A current I=2t flows in the smaller loop. Neglecting self-inductance of the larger loop,
a. find the mutual inductance of the two coils,
b. find the emf induced in the larger coil,
c. if the resistance of the larger loop is R, find the current in it as a function of time.

View SolutionFigure shows two concentric coplanar coils with radii a and b(a<<b). A current I=2t flows in the smaller loop. Neglecting self-inductance of the larger loop,
a. find the mutual inductance of the two coils,
b. find the emf induced in the larger coil,
c. if the resistance of the larger loop is R, find the current in it as a function of time.

View SolutionIn the figure shown a conducting rod of length l, resistnace R and mass m is moved with a constant velocity v.The magnetic field B varies with time t as B=5t, where t is time in second.At t=0 the area of the loop containing capacitor and the rod is zero and the capacitor is uncharged.The rod started moving at t=0 on the fixed smooth conducting rails which have negligible resistance.Find (i)The current in the circuit as a function of time t.
(ii)If the above system is kept in vertical plane such that the rod can move vertically downward due of gravity and other parts are kept fixed and B=constant =B0.then find the maximum current in the circuit.
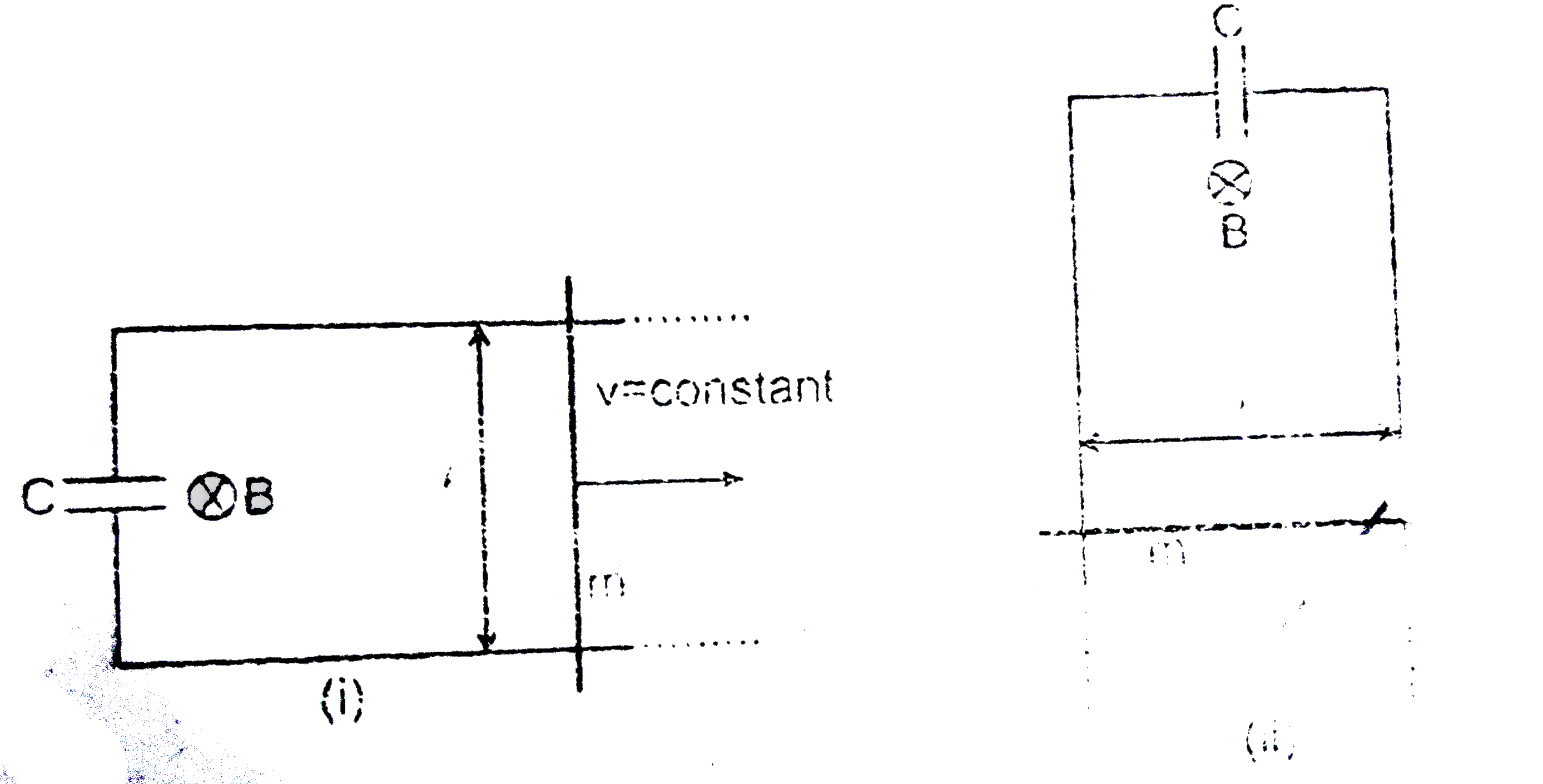
View SolutionFigure shows tow concentric coplanar coils with radii a and b (a<<b). A current i=2t flows in the smaller loop. Neglecting self inductance of larger loop

(a) Find the mutual inductance of two coils.
(b) Find the emf induced in the larger coil
(c) If the resistance of the larger loop is R find the current in it as a function of time.
View SolutionIn the following circuit (Fig.)the switch is closed at t=0. Intially, there is no current in inductor. Find out the equation of current in the inductor coil as s function of time.
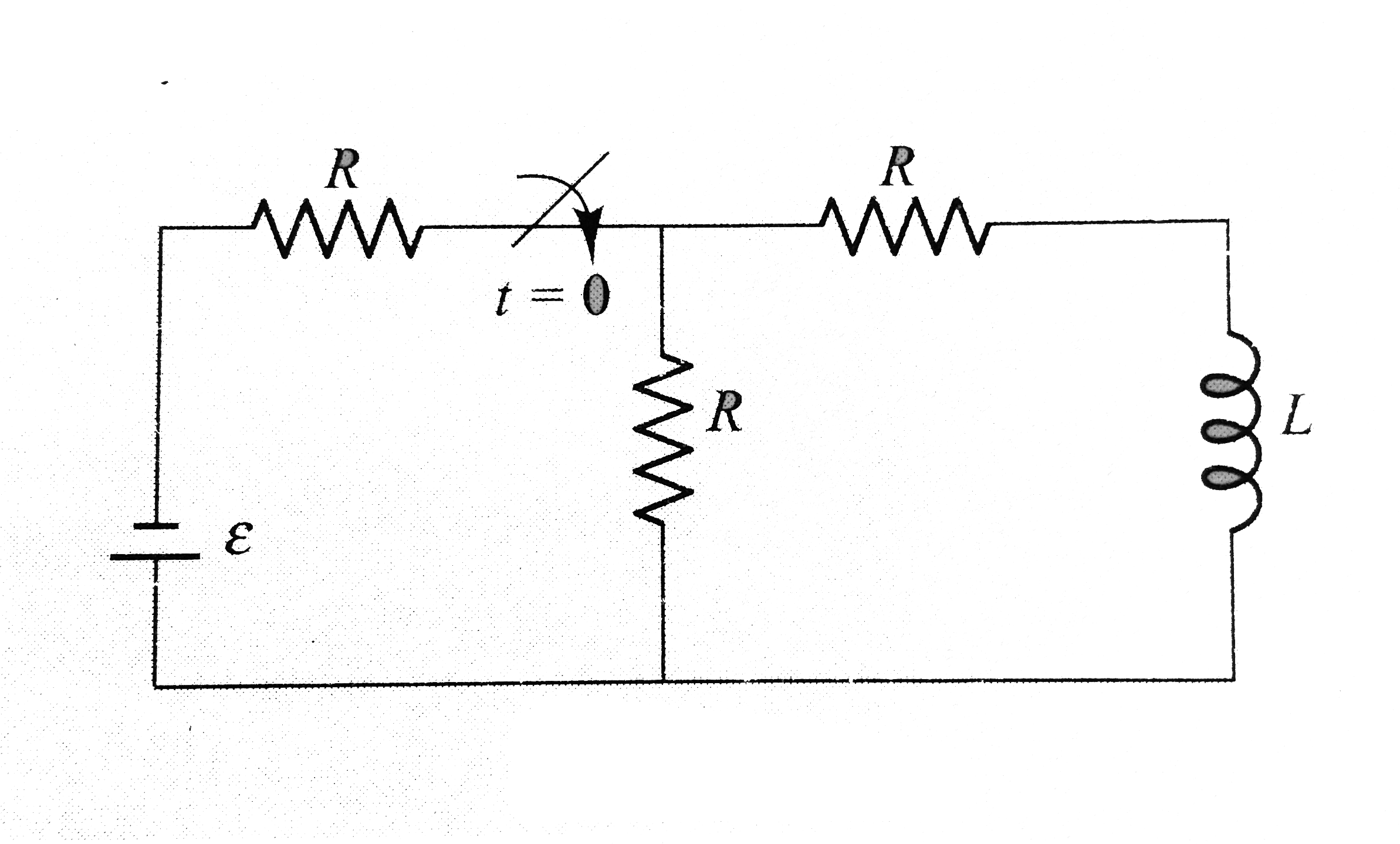
View SolutionIn the circuit diagram shown, initially there is no energy in the inductor and the capacitor, The switch is closed at t=0. Find the current I as a function of time if R=√L/C
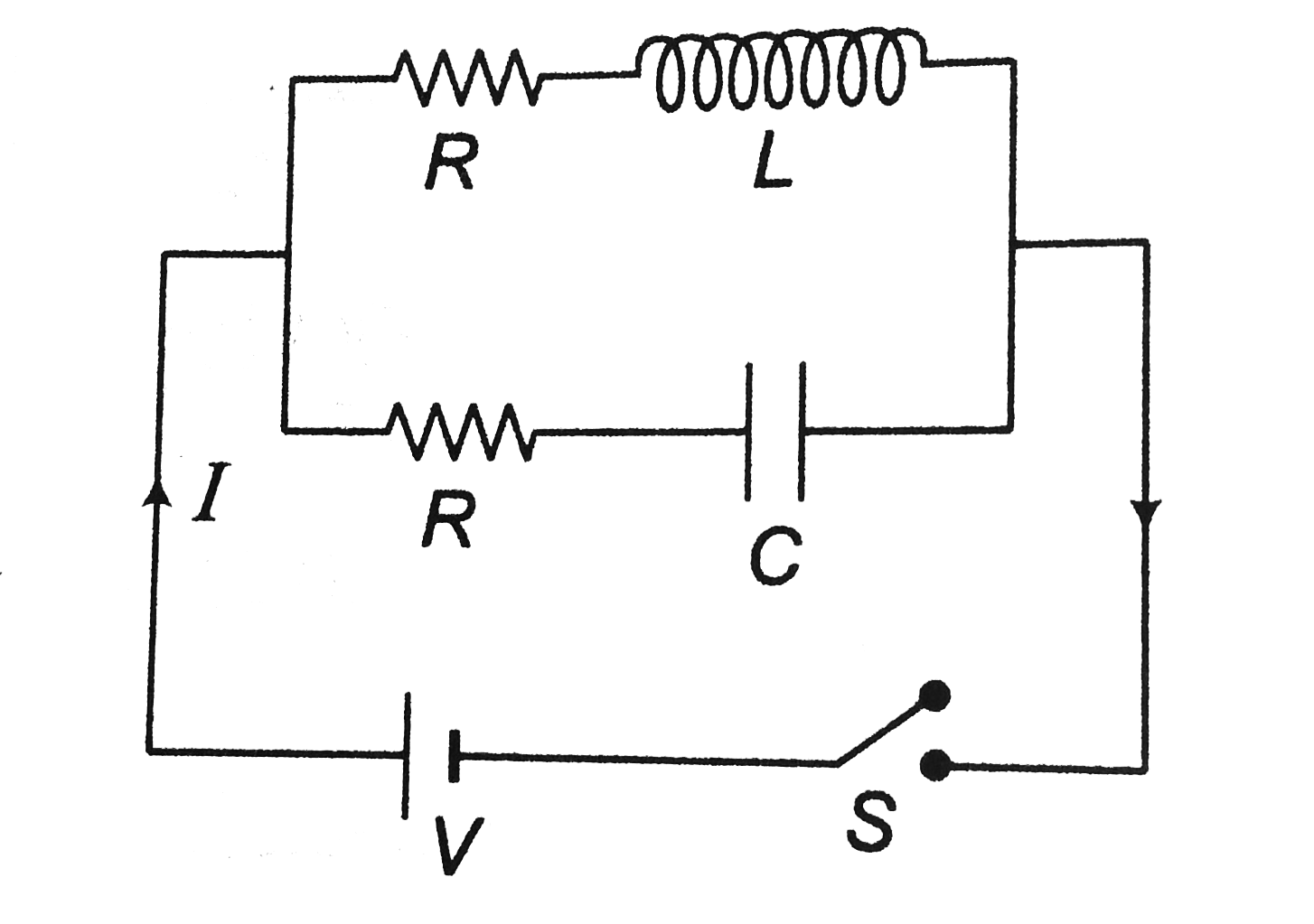
View Solution
