An elastic ball of mass 'm' is suspended from a fixed point by an inextensible string. A small particle of same mass m, moving downwards at an angle of 37∘ with the vertical lits the ball directly with the velocity v0. If the coefficient of restitution is 4/5,
(i) find the velocity of the ball just after the impact.
(ii) determine the impulsive tension(i.e impulse) in the string at the instant of collision.
To solve the problem step by step, we will analyze the collision between the two balls and apply the principles of conservation of momentum and the coefficient of restitution.
Step 1: Analyze the Situation
We have two balls of mass m. One ball (let's call it Ball A) is stationary and suspended from a string, while the other ball (Ball B) is moving downward at an angle of 37° with the vertical with an initial velocity v0.
Step 2: Resolve the Velocity of Ball B
The velocity of Ball B can be resolved into two components:
- Vertical component: \( v_{B_y} = v_0 \cos(37^\circ) \)
- Horizontal component: \( v_{B_x} = v_0 \sin(37^\circ) \)
Given that \( \cos(37^\circ) = \frac{4}{5} \) and \( \sin(37^\circ) = \frac{3}{5} \), we can express these components as:
- \( v_{B_y} = v_0 \cdot \frac{4}{5} \)
- \( v_{B_x} = v_0 \cdot \frac{3}{5} \)
Step 3: Apply the Coefficient of Restitution
The coefficient of restitution \( e \) is given as \( \frac{4}{5} \). This relates the velocities of the two balls before and after the collision:
\(
e = \frac{V_A - V_B}{v_B - v_A}
\)
Where:
- \( V_A \) = velocity of Ball A after the collision
- \( V_B \) = velocity of Ball B after the collision
- \( v_B \) = velocity of Ball B before the collision
- \( v_A \) = velocity of Ball A before the collision (which is 0 since it is stationary)
Substituting the known values:
\(
\frac{4}{5} = \frac{V_A - V_B}{v_0 \cdot \frac{4}{5} - 0}
\)
Step 4: Solve for the Velocities After Collision
From the equation above, we can rearrange it to find the relationship between \( V_A \) and \( V_B \):
\(
4(v_0 \cdot \frac{4}{5}) = 5(V_A - V_B)
\)
\(
4v_0 \cdot \frac{4}{5} = 5V_A - 5V_B
\)
\(
\frac{16v_0}{5} = 5V_A - 5V_B
\)
\(
5V_A = 5V_B + \frac{16v_0}{5}
\)
\(
V_A = V_B + \frac{16v_0}{25}
\)
Step 5: Apply Conservation of Momentum
Using the conservation of momentum for the system:
\(
m v_B + m \cdot 0 = m V_A + m V_B
\)
This simplifies to:
\(
v_B = V_A + V_B
\)
Thus:
\(
0 = V_A - v_B
\)
Substituting \( V_A \) from the previous step:
\(
0 = (V_B + \frac{16v_0}{25}) - v_B
\)
This implies:
\(
V_B = \frac{16v_0}{25}
\)
Step 6: Find the Velocity of Ball A
Substituting \( V_B \) back into the equation for \( V_A \):
\(
V_A = \frac{16v_0}{25} + \frac{16v_0}{25} = \frac{32v_0}{25}
\)
Step 7: Calculate the Impulsive Tension
The impulsive tension in the string can be found using the change in momentum of Ball A:
\(
\text{Impulse} = m(V_A - 0) = m \cdot V_A = m \cdot \frac{32v_0}{25}
\)
Final Answers
(i) The velocity of the ball just after the impact \( V_A = \frac{32v_0}{25} \).
(ii) The impulsive tension (impulse) in the string at the instant of collision \( = m \cdot \frac{32v_0}{25} \).
We have two balls of mass m. One ball (let's call it Ball A) is stationary and suspended from a string, while the other ball (Ball B) is moving downward at an angle of 37° with the vertical with an initial velocity v0.
The velocity of Ball B can be resolved into two components:
- Vertical component: \( v_{B_y} = v_0 \cos(37^\circ) \)
- Horizontal component: \( v_{B_x} = v_0 \sin(37^\circ) \)
- \( v_{B_y} = v_0 \cdot \frac{4}{5} \)
- \( v_{B_x} = v_0 \cdot \frac{3}{5} \)
The coefficient of restitution \( e \) is given as \( \frac{4}{5} \). This relates the velocities of the two balls before and after the collision:
\(
e = \frac{V_A - V_B}{v_B - v_A}
\)
Where:
- \( V_A \) = velocity of Ball A after the collision
- \( V_B \) = velocity of Ball B after the collision
- \( v_B \) = velocity of Ball B before the collision
- \( v_A \) = velocity of Ball A before the collision (which is 0 since it is stationary)
\(
\frac{4}{5} = \frac{V_A - V_B}{v_0 \cdot \frac{4}{5} - 0}
\)
From the equation above, we can rearrange it to find the relationship between \( V_A \) and \( V_B \):
\(
4(v_0 \cdot \frac{4}{5}) = 5(V_A - V_B)
\)
\(
4v_0 \cdot \frac{4}{5} = 5V_A - 5V_B
\)
\(
\frac{16v_0}{5} = 5V_A - 5V_B
\)
\(
5V_A = 5V_B + \frac{16v_0}{5}
\)
\(
V_A = V_B + \frac{16v_0}{25}
\)
Using the conservation of momentum for the system:
\(
m v_B + m \cdot 0 = m V_A + m V_B
\)
This simplifies to:
\(
v_B = V_A + V_B
\)
Thus:
\(
0 = V_A - v_B
\)
Substituting \( V_A \) from the previous step:
\(
0 = (V_B + \frac{16v_0}{25}) - v_B
\)
This implies:
\(
V_B = \frac{16v_0}{25}
\)
Substituting \( V_B \) back into the equation for \( V_A \):
\(
V_A = \frac{16v_0}{25} + \frac{16v_0}{25} = \frac{32v_0}{25}
\)
The impulsive tension in the string can be found using the change in momentum of Ball A:
\(
\text{Impulse} = m(V_A - 0) = m \cdot V_A = m \cdot \frac{32v_0}{25}
\)
(i) The velocity of the ball just after the impact \( V_A = \frac{32v_0}{25} \).
Topper's Solved these Questions
Similar Questions
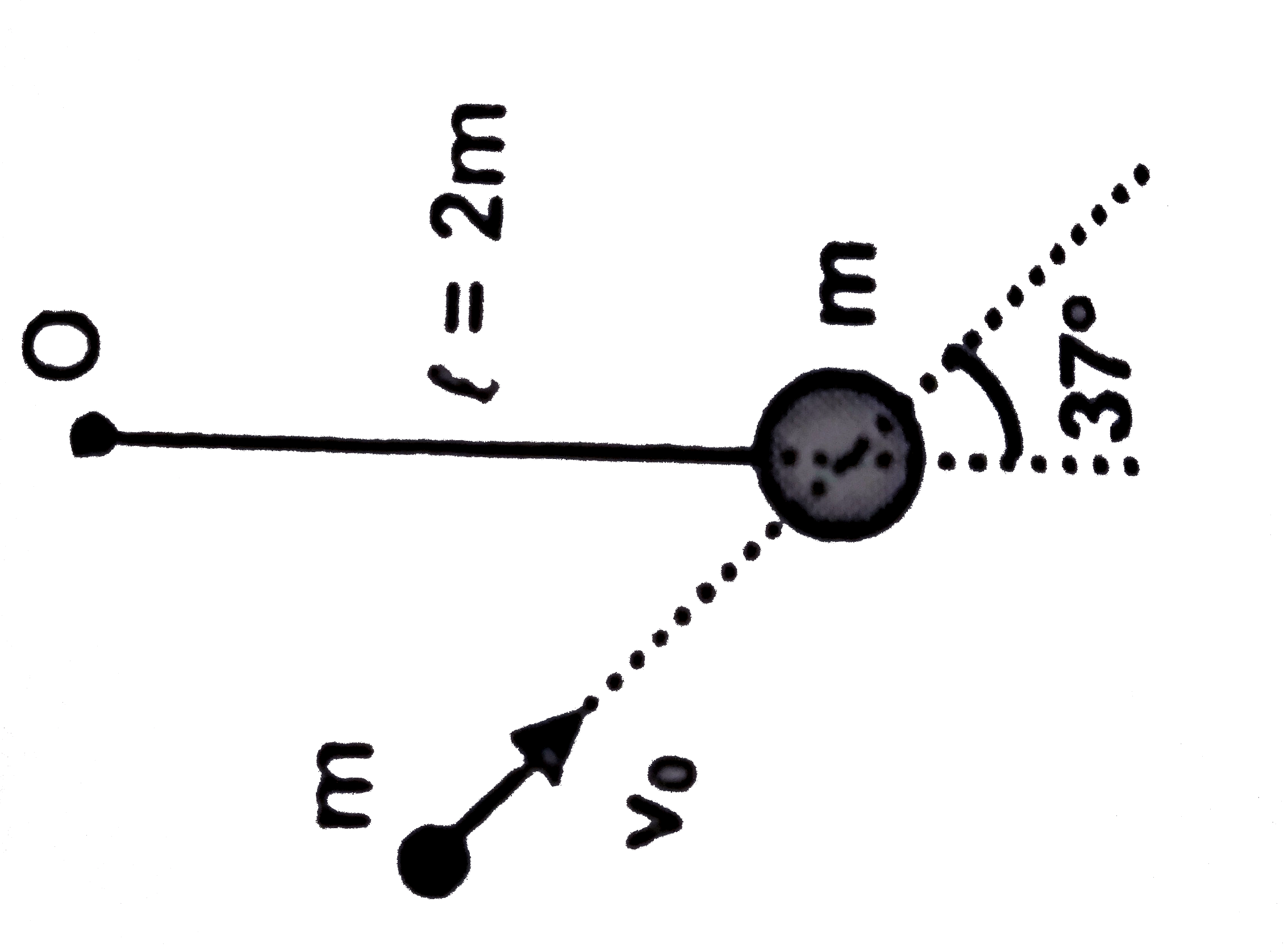
An elastic ball of mass 'm' is suspended from a fixed point 'O' by an inextensible string of length 2m. A small particle of mass m moving downward at angle of 37∘ with the vertical hits the ball with v0. The coefficient of restitution for collision is 4/5. the velocity of the particle v0 such that ball just comoplete on revolution after the collision.
View SolutionA glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View Solution
Knowledge Check
A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eBe−1e+1C1+e1−eDe+1e−1A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eB1+e1−eCe−1e+1De+1e−1
A ball of mass 2kg moving with speed 5m/s collides directly with another ball of mass 3kg moving in the same direction with speed 4m/s. The coefficient of restitution is 2/3. Find the velocities of both ball after the collision.
View SolutionThe first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
View SolutionA small ball of mass m collides with as rough wal having coeficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves wilth angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.

View SolutionA ball P is moving with a certain velocity v, collides head-on with another ball Q of same mass at rest. The coefficient of restitution is 1/4, then ratio of velocity of P and Q just after the collision is
View SolutionA ball collides with a frictionless wall with velocity u as shown in the figure. Coefficient of restitution for the impact is e.
(a) Find expression for the velocity of the ball immediately after the impact.
(b) If impact is perfectly elastic what do you observe?
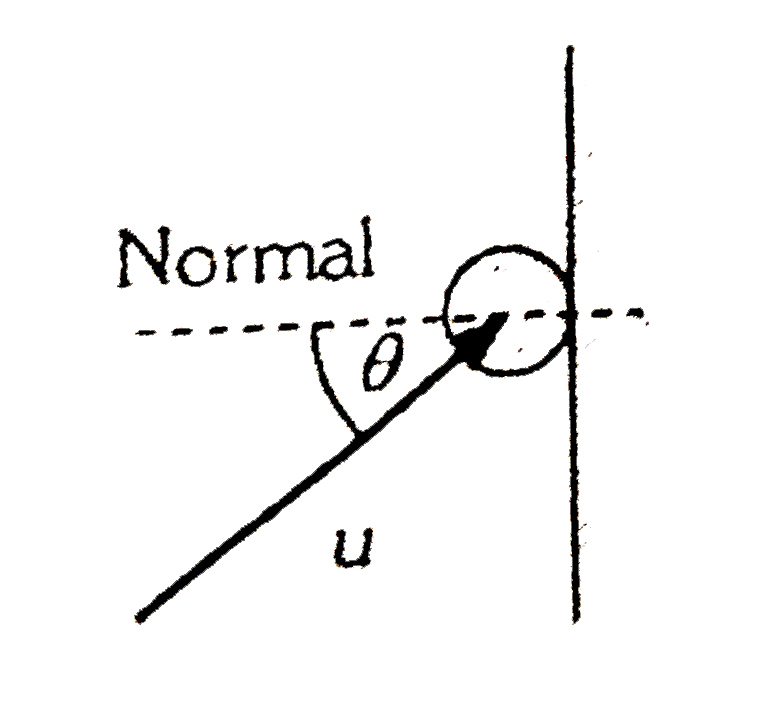
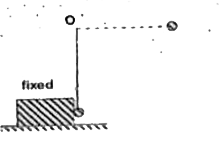
View SolutionA small ball is suspended from a fixed point 'O' by means of a light and inextensible string of length 'l'. The ball is first taken aside such that string becomes horizontal and then released from rest. At the borrom it collides with a fixed obstacle. The co-efficient of restitution is 'e'. Find the maximum angular deflection of the string after nth collision.
View Solution
