A carpet of unit mass an unit length is laid on the floor. One end of the carpet is bent back and then pulled backwards with constants. Unit velocity, just above the part of the carpet which is still at rest on the floor. Find the speed of the centre of mass of the moving part. What is the minimum force needed to pull the moving part ?

If the end of the folded part of the carpet is at a distance of x from the origin, the centre of mass of the folded part (which is moving) is at 3x/4 and hence has a speed of 0.75m/s.
Now, force =dpdt=d(mv)dt=m(dvdt)=0+v(dmdt)=0.5N
Note that the moving part of the carpet starts from the origin and the whole carpet will be moving when it reaches x=2 after two units of time giving (dmdt)=0.5
Note that the moving part of the carpet sets the next part into motion some energy is dissipated as heat.
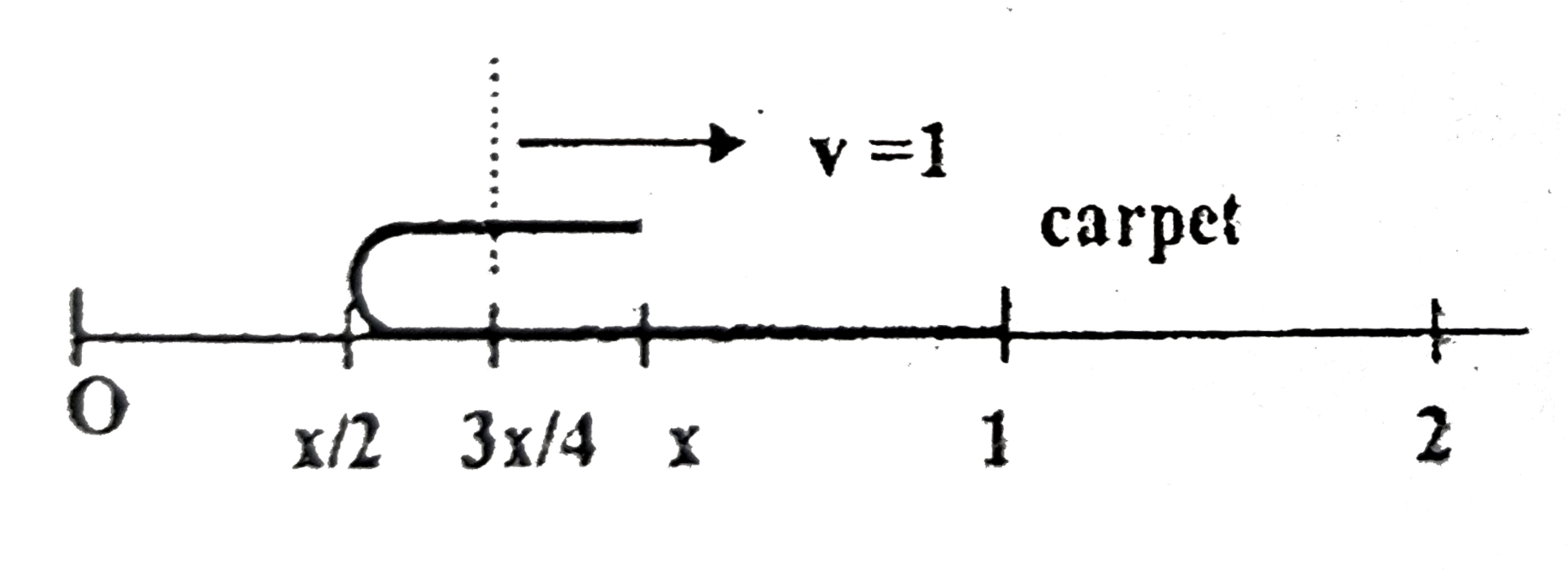
Topper's Solved these Questions
Similar Questions
A long thin pliable carpet is laid on the floor. One end of the carpet is bent back and then pulled backwards with constant unit velocity just above the part of the carpet which is still at rest on the floor. Speed of centre of mass of the moving part is (2×xmm)/sec. Then find x75?

View SolutionA block of mass m rests on a rough floor . The coefficient of friction between the block and the floor is μ
a. Two boys apply force P at an angle θ to the horizontal. One of them pushes the block , the other one pulls. Which one would reqire less efferts to cause impending motion of the block?
b. What is the minimum force required to move the block by pulling it ?
c. Shown that the block is pushes at a certain angle θ0 it cannot be moved fro whatever the value of P be
View SolutionA line of fixed length 2 units moves so that its ends are on the positive x-axis and that part of the line x+y=0 which lies in the second quadrant. Then the locus of the midpoint of the line has equation.
View SolutionA chain of mass m and length L is held at rest on smooth horizontal surface such that a part I of the chain is hanging vertically from the table. If the chain is let go, what is its speed as its end just leaves the horizontal surface?
View SolutionA car moves at a constant speed on a straigh but hilly road. One section has a crest and dip of the 250m radius.
(a) As the car passes over the crest the normal force on the car is half the 16kN weight of the car. What will the noraml force on the car its passes through th ebottom of the dip?
(b) What is the greatest speed at which the car can move without leaving the road at the top of the hill ?
(c) Moving at a speed found in part (b) what will be the normal force on the car as it moves through the bottom of the dip? (Take, g=10m/s2)
View SolutionA puck of mass m is moving in a circle at constant speed on a frictionless table as shown in the figure . The puck is connected by a string to a suspended bob, also of mass m, which is at rest below the table. Half of the length of the string is above the tabletop and half below. What is the magnitude of the centripetal acceleration of the moving puck ? Let g be the acceleration due to gravity.

View SolutionA body of mass M moving with velocity V explodes into two equal parts. If one comes to rest and the other body moves with velocity v, what would be the value of v ?
View SolutionA plank of mas M and length L is at rest on as frictionless floor. The top surface of the plank has friction. At one end of it a man of mass m is standing as shown in figure. If the man walks towards the other end the find the distance, which the plank moves a till the man reaches the centre of the plank. b. till the man reaches the other end of the plank.

View SolutionA uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
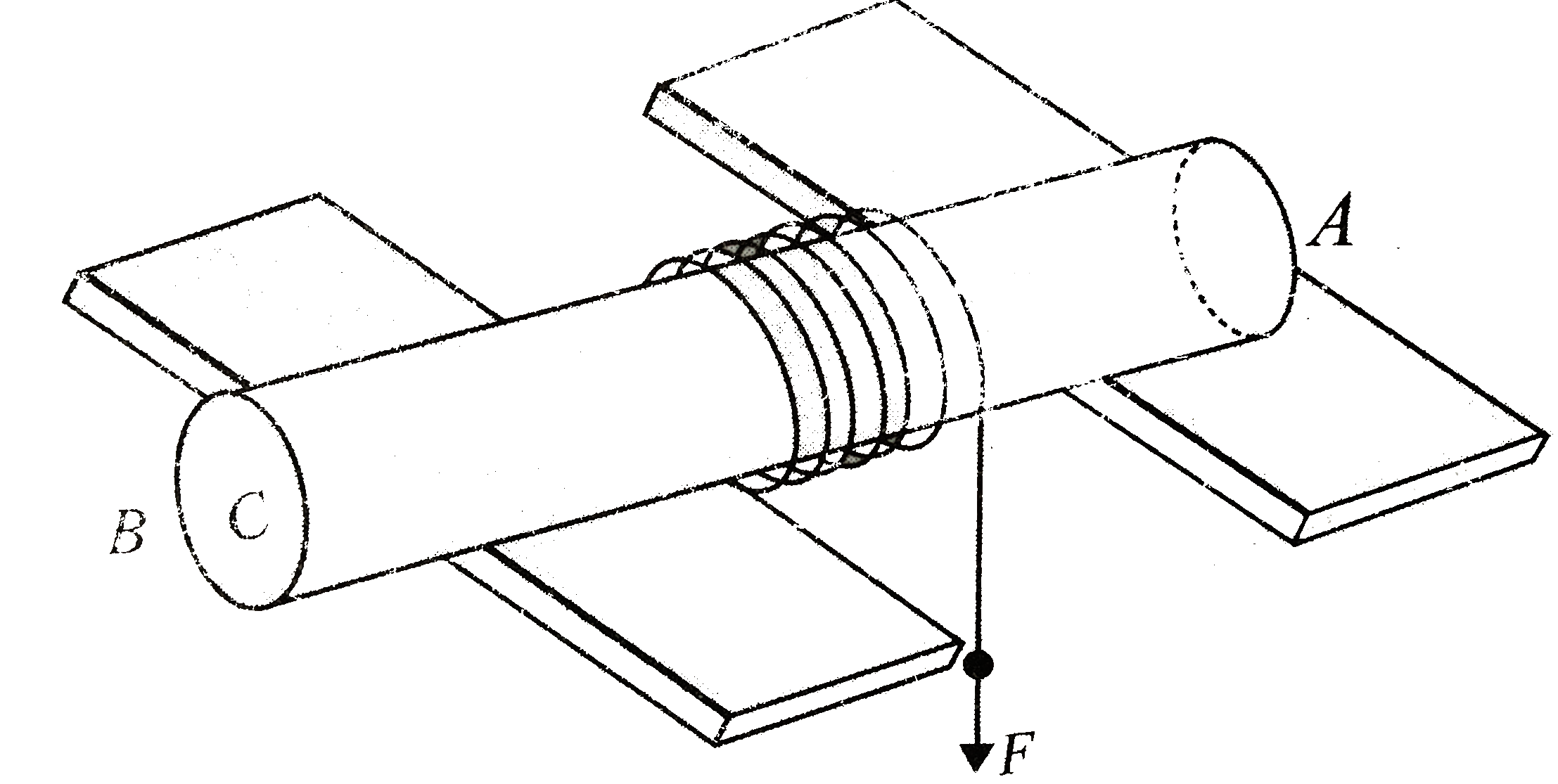
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?
View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View Solution
