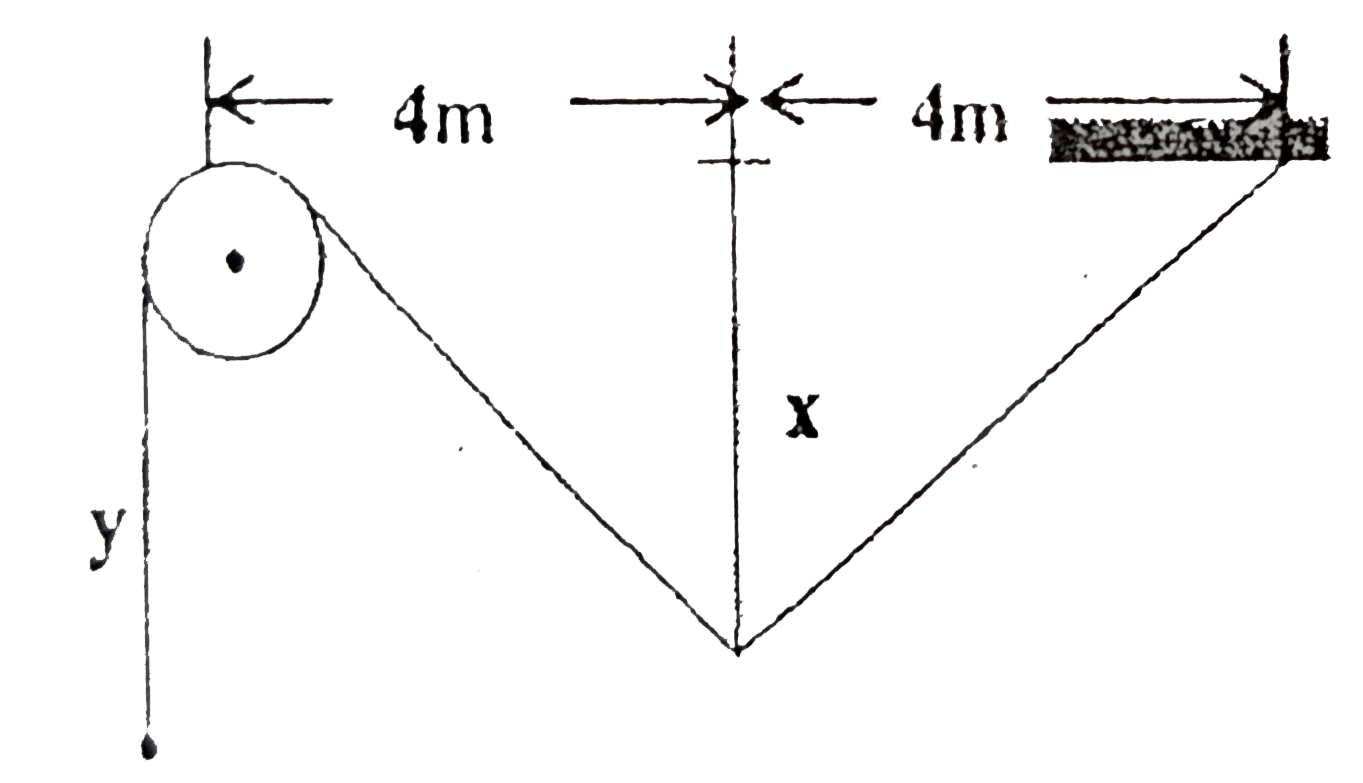
The system of mass A and B shown in the figure is released from rest with x=0, determine the velocity of mass B when x=3m. Also find the maximum displacement of mass B.

Constraint relation gives
2√x2+16+y=c
Differentiating w.r.t. time, we get
dydt=−x√x2+dtdxdt
Let dxdt=v= velocity of B
∴dydt= velocity of A=−x√x2+16v
Minus sign indicates that it in upward direction.
∴ Using energy conservation
mg.3−mg√2.2=12mv2+12m√2(v.35)2
⇒(3−√2)g=v2(25√2+9)50√2
⇒v=
⎷(3−√2)(50√2)25√2+9g=5m/s
Let x1 be the maximum displacement of B, then
mgx1−mg√22[√x21+16−4]=0
⇒x1=8√2m.
Topper's Solved these Questions
Similar Questions
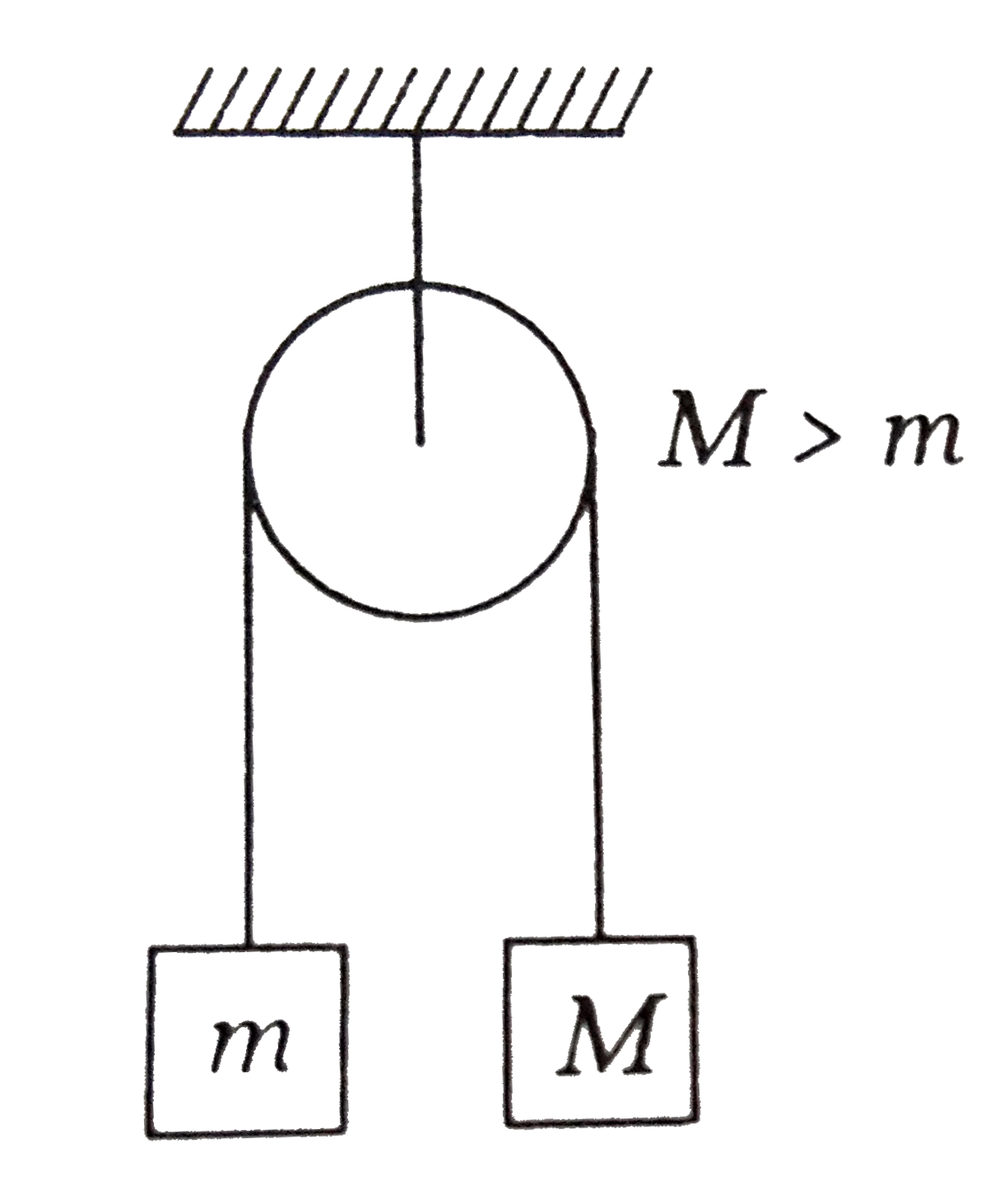
The system shown in the figure is released from rest. At the instant when mass M has fallen through a distance h, the velocity of m will be
View SolutionFind the velocity of center of mass of the system shown in the figure.

View SolutionBlock A in the figure is released from rest when the extension in the spring is x0(x0<mg/k). The maximum downward displacement of the block is (there is no friction) :

View SolutionThe simple pendulum A of mass mA and length l is suspended from the trolley B of mass mB. If the system is released from rest at θ=0, determine the velocity vB of the trolley when θ=90°. Friction is negligible.

View SolutionIf the system is released from rest, determine the speeds of both masses after B has moved 1 m. Neglect friction, the masses of pulleys and inextensible string.
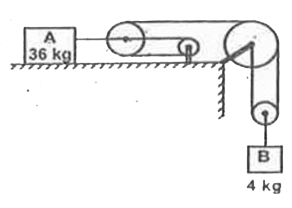
View SolutionA system is shown in the figure. Block A moves with velocity 10m/s. The speed of the mass B will be :
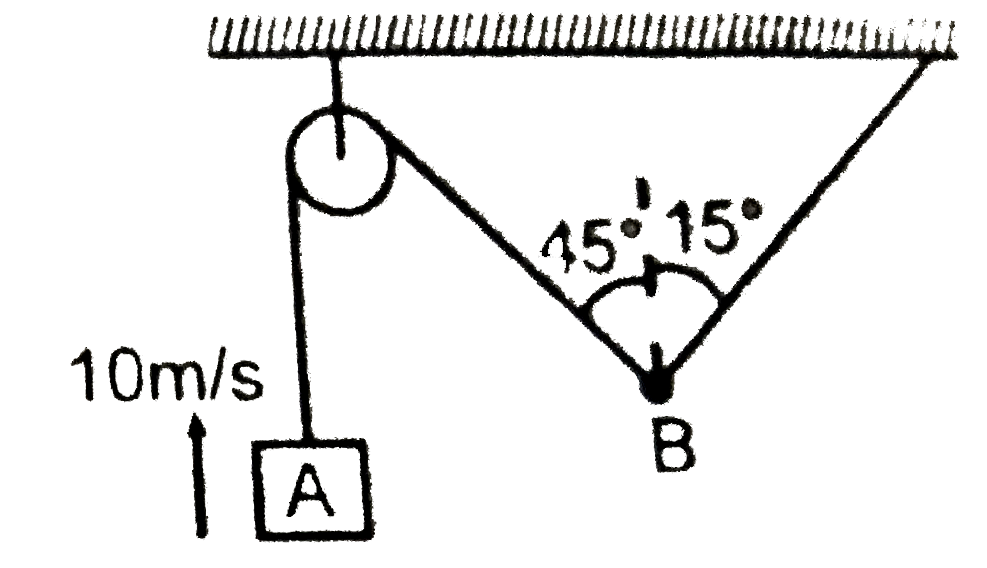
View SolutionAs shown in the figure, a disc of mass m is rolling without slipping with angular velocity ω. When it crosses point B disc will be in

View SolutionTwo smooth wedges of equal mass m are placed as shown in figure. All surfaces are smooth. Find the velocities of A & B when A hits the ground.
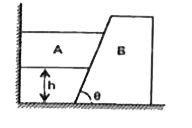
View SolutionFind the mass m in the figure for the system to be at rest
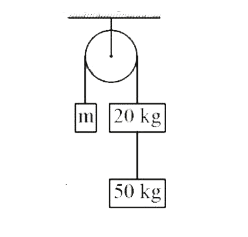
View Solution
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View Solution

