The arrangement shown in figure is at rest. An ideal spring of natural length l0 having spring constant k=220Nm−1, is connected to block A. Blocks A and B are connected by an ideal string passing through a friction less pulley. The mass of each block A and B is equal to m=2kg when the spring was in natural length, the whole system is given an acceleration →a as shown. If coefficient of friction of both surfaces is μ=0.25, then find the maximum extension in 10(m) of the spring. (g=10ms−2).
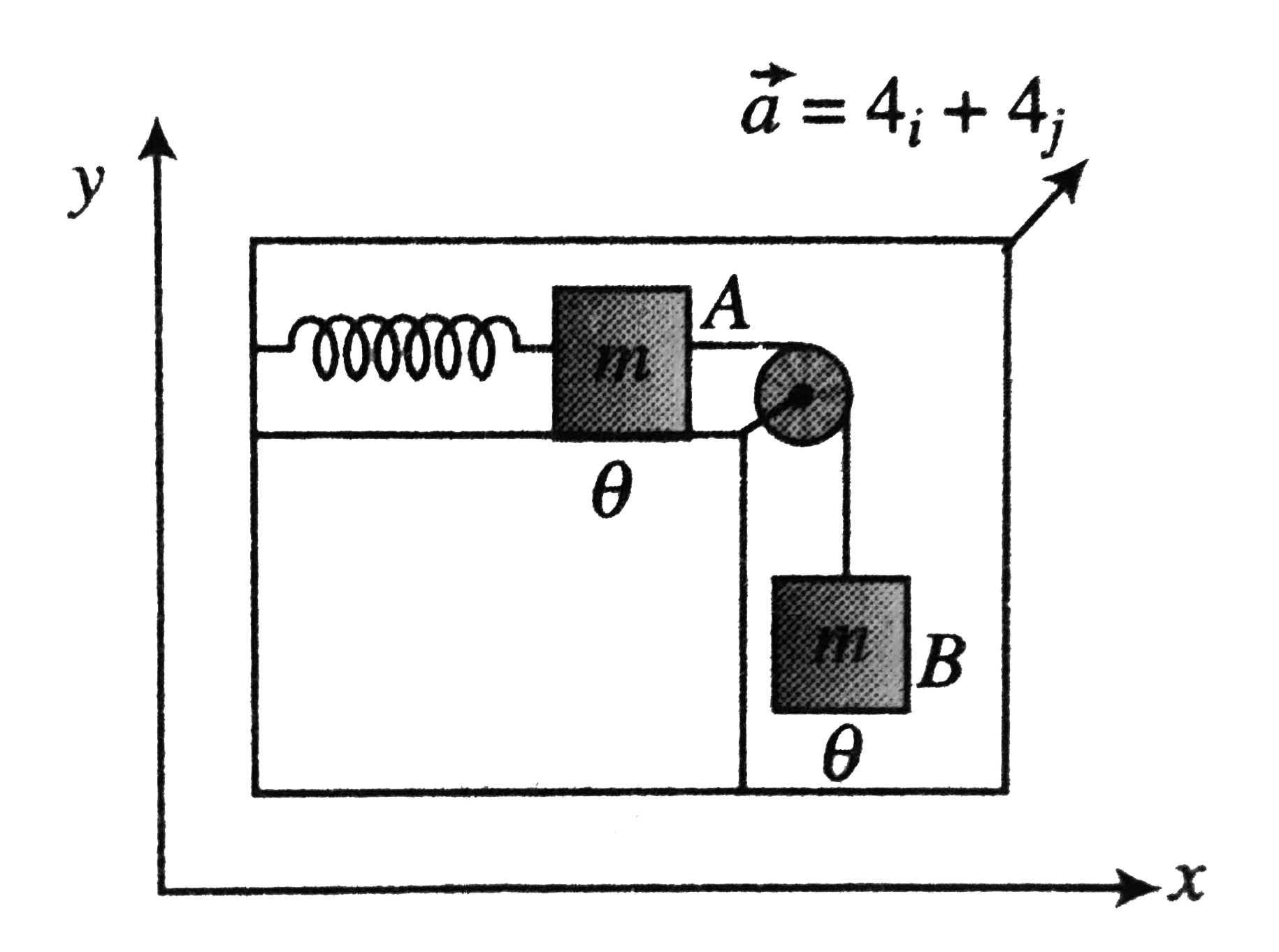
Case I : a=(4ˆi+4ˆj)m/s2, ax=4m/s2, ay=4m/s2
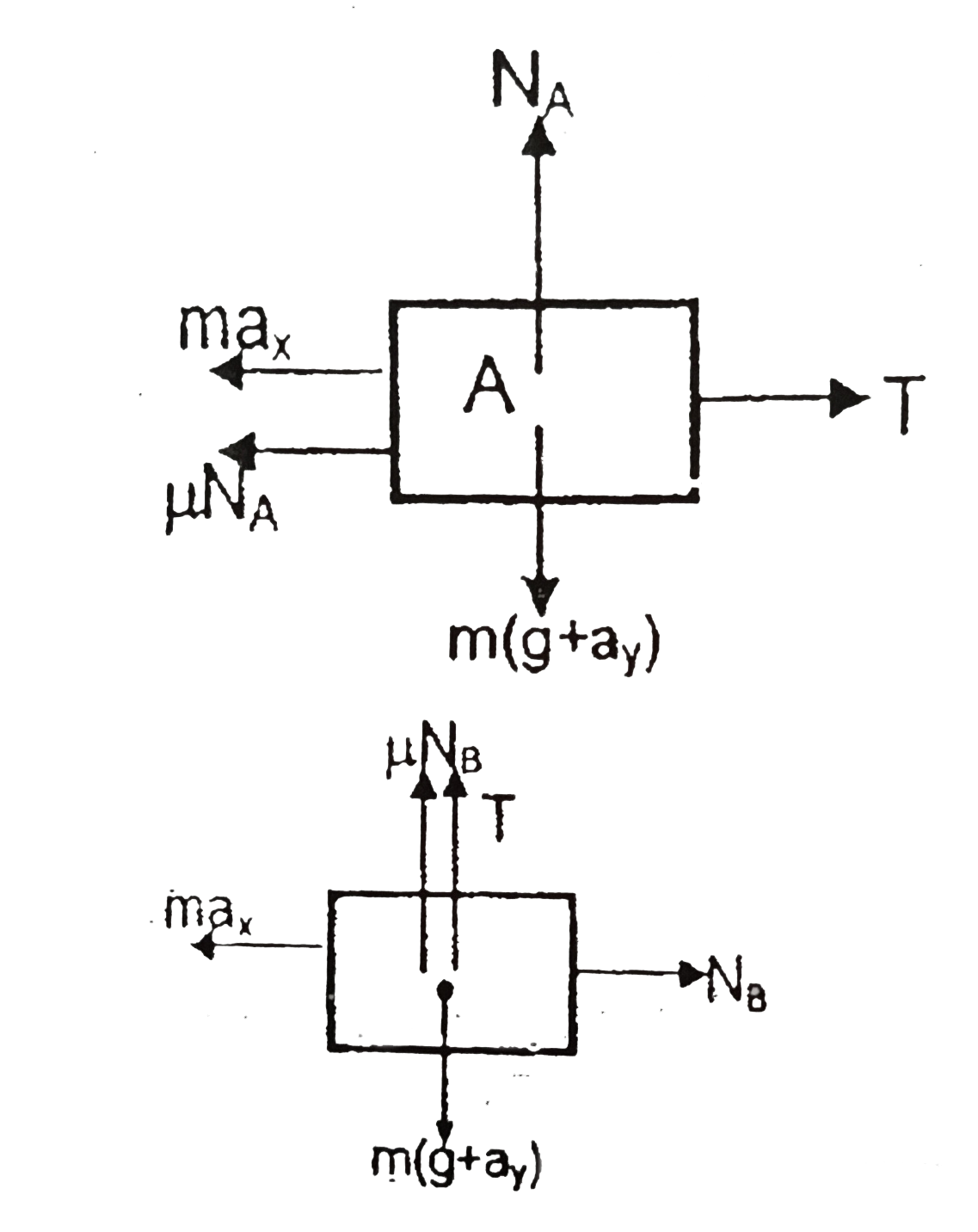
FBD of blocks A and B
NA=m(g+ay)=28N
T=max+μNA=8+28μ…..(1)
NB=max=8N
T+μNB=m(g+ay)
T+8μ=28…..(2)
From Eqs.(1) and (2), μmin=5/9
Case II : Let extension of spring =x, μ'=(5/9)×(9/35)=1/7
From work energy theorem :
mgx−μ'NAx−μ'NBx−maxx+mayx=1/2kx2
20x−(1/7)x×(28x)−(1/7)x×(8x)=25x2
x=0.6m
Topper's Solved these Questions
Similar Questions
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

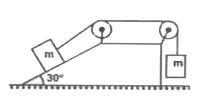
View SolutionTwo blocks, each having mass m, are connected with an ideal string through ideal pulleys on a frictionless fixed wedge as shown in the figure. The acceleration of the blocks is
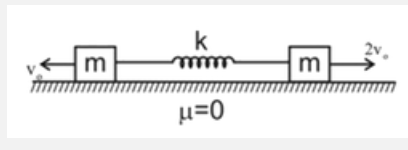
View SolutionThe figure shows two blocks of mass m each, connected by an ideal unstretched spring and then placed on a frictionless floor. If the blocks are given velocities v0and2v0 as shown, then the maximum extension in the spring is
View SolutionTwo blocks are connected by a long inextensible string passing over an ideal pulley as shown in the figure. If the system is released from rest then the common speed of blocks when block m2 moves a distance I will be
View SolutionA block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) in gravity free space. Find the elongation in spring.
View SolutionConsider the condition shown in the figure. Pulley is massless and frictionless, springs are massless. Both the blocks are released with the springs in their natural lengths. Choose the correct options.
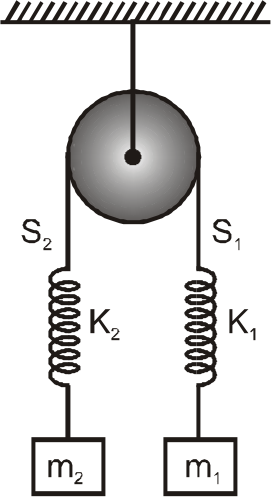
View SolutionIn the situations shown in the figure surfaces are frictionless. Find the maximum extension of the springs if blocks are initially at rest and springs are initially in natural lengths.

View SolutionA system consists of block A and B each of mass m connected by a light spring as shown in the figure with block B in contact with a wall. The block A compresses the spring by 3mg/k from natural length of spring and then released from rest. Neglect friction anywhere
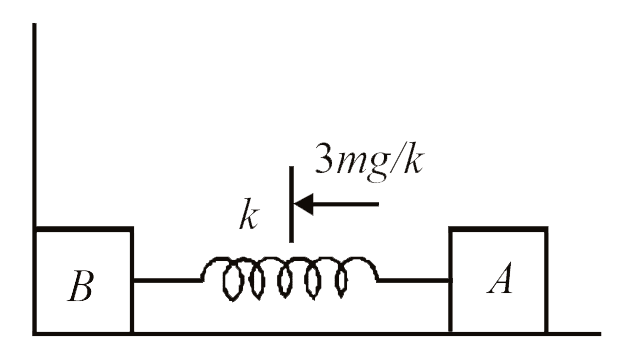
Acceleration of centre of mass of system comprising A and B just after A is released is
View SolutionA system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
 .
.
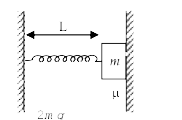
View SolutionA block of mass m is pressed against a wall by a spring as shown in the figure. The spring has natural length , l(l>L), and the coefficient of friction between the block and the wall is μ . The minimum spring constant K necessary for equilibrium is:
View Solution