Two beads of masses m1 and m2 are connected to each other by massless string. Both beads are free to mover over fixed smooth circular loop in vertical plane. At any instant they are in the position shown and subtends angle 90∘ at centre. Find tangential accelerations of both beads and tension in the string if string remains taut.

Let a1 and a2 be the tangential accelerations of two beads respectively. Then for bead A
m1gsin30∘+Tsin45∘=m1a1…..(i)
For bead B
m2gsin60∘−Tsin45∘=m2a2…..(ii)
since string remains taut
∴a1cos45∘=a2cos45∘
(Acceleration along string remains same)
⇒a1=a2=a
∴ from (i) and (ii)
a=g(m1+√3m2)2(m1+m2)
T√2=m1g(m1+√3m2)2(m1+m2)−m1g2
T=(√3−1)(m1m2g)√2(m1+m2)

Topper's Solved these Questions
Similar Questions
Two beads of equal masses m are attached by a string of length √2a and are free to move in a smooth circular ring lying in a vertical plane as shown in figure. Here a is the radius of the ring. Find the tension and acceleration of B just offer the heads are released to move.

View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
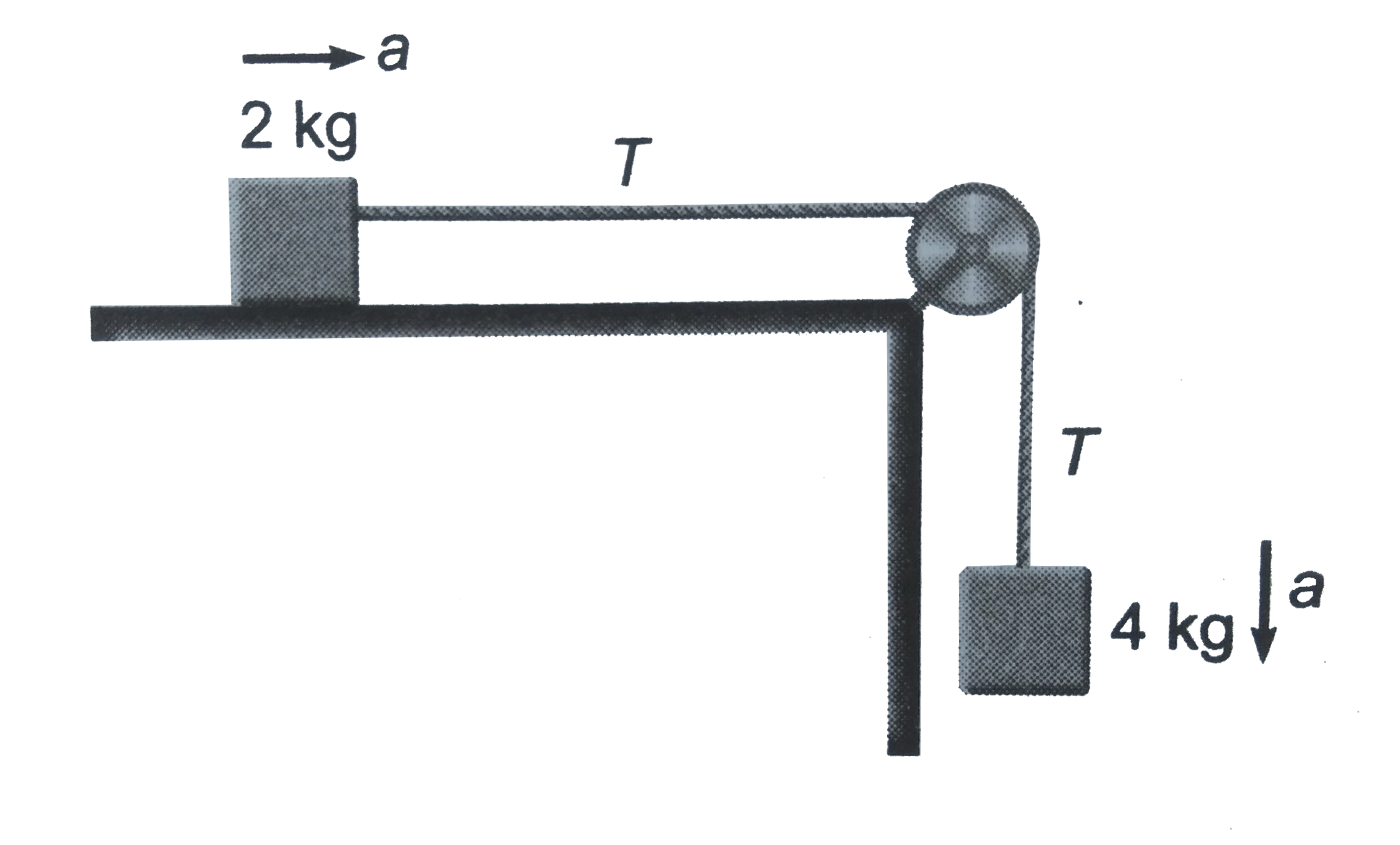
View SolutionIn the system shown in figure all surfaces are smooth. Strings is massless and inextensible.Find acceleration of the system and tension T in the string (g=10m/s2)
View SolutionTwo beads of masses m1andm2 connected by an inextensible string are kept at rest at the horizontal diametrical points of a fixed smooth vertical semicircular tube. If the beads are released from the given position, find their speeds as the function of vertical distance y converted by mass m2.
View SolutionTwo beads of mass 2m and m, connected by a rod of length l and of negligible mass are free to move in a smooth vertical circular wire frame of radius l as shown. Initially the system is held in horizontal position ( Refer figure )

If the rod is replaced by a massless string of length l and the system is released when the string is horizontal then :
View SolutionTwo beads of masses m1andm2 connected by an inextensible string are kept at rest at the horizontal diametrical points of a fixed smooth vertical semicircular tube. If the beads are released from the given position, find their speeds as the function of vertical distance y converted by miss m2.

View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
View SolutionTwo particles of masses m and M(M>m) are connected by a cord that passes over a massless, frictionless pulley. The tension T in the string and the acceleration a of the particles is
View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View Solution