An aeroplane is flying horizontally at a height of $\frac{2}{3}$ km with a velocity of 500 km/h. Find the rate at which it is receding from a fixed point on the ground which it passed over 2 min ago.

Video Solution

Text Solution

Verified by Experts

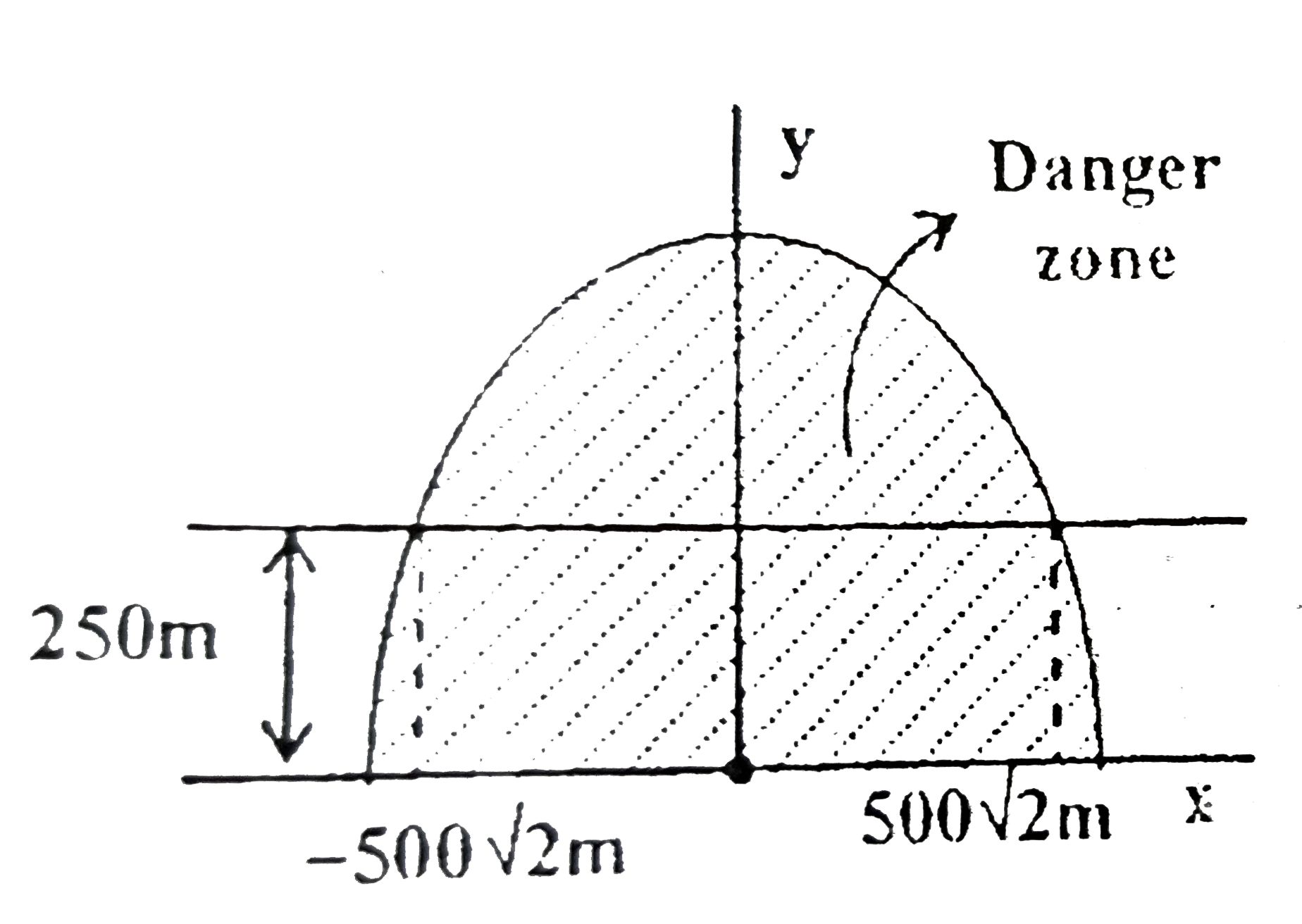
We first find the area in which the cannon shell can reach. The equation of trajectory for cannon shell is
$y = x tan θ - \frac{\frac{1}{2} g x^{2}}{u^{2}} {sec}^{2} θ$ .......( $1$ )
For maximum $y$ for a given value of $x$ -
$\frac{d y}{d (tan θ)} = x - \frac{\frac{1}{2} g x^{2}}{u^{2}} (2 tan θ) = 0 \Rightarrow tan θ = \frac{u^{2}}{g x}$
Putting in equation ( $1$ )
$y_{max} = x \frac{u^{2}}{g x} - \frac{\frac{1}{2} g x^{2}}{u^{2}} [1 + \frac{u^{4}}{g^{2} x^{2}}] = \frac{u^{2}}{2 g} - \frac{\frac{1}{2} g x^{2}}{u^{2}}$
$∴$ The cannon shell can hit an area given by
$y \leq \frac{u^{2}}{2 g} - \frac{\frac{1}{2} g x^{2}}{u^{2}}$
Given in the problem $y = 250 m$ , $u = 100 m / s$ , $g = 10 m / s$ .
Putting these value we get,
$\frac{x^{2}}{2000} \leq 250 \Rightarrow - 500 \sqrt{2} \leq x \leq 500 \sqrt{2}$
$∴$ Plane is in danger for a period of $\frac{1000 \sqrt{2}}{500} = 2 \sqrt{2} sec$

Updated on:21/07/2023

An aeroplane flying horizontally with a speed of 360 km $h^{- 1}$ releases a bomb at a height of 490 m from the ground. If g = 9. 8 m $s^{- 2}$ , it will strike the ground at
A10 km
B100 km
C1 km
D16 km
A bomb is dropped from an aeroplane flying horizontally with a velocity 720 km/hr at an altitude of980 m. The bomb will hit the ground after a time
A1 sec
B7.2 sec
C14.15 sec
D0.15 sec