Two particles A and B are situated at point (60,0) at t=0. The particle A move on a circle given by X2+Y2=3600 and with a speed 6πm/s, while B moves with a constant velocity.
Find the velocity of B so that the collision takes places between A and B at point (60,0).
To solve the problem, we need to find the velocity of particle B such that it collides with particle A at the point (60, 0). Let's break down the solution step by step.
Step 1: Understand the motion of particle A
Particle A moves on a circle defined by the equation x2+y2=3600. The radius of this circle is 60 meters (since 602=3600). Particle A starts at the point (0, 60) and moves with a speed of 6π m/s.
Step 2: Determine the distance A travels to reach (60, 0)
To find the distance that particle A travels to reach the point (60, 0), we need to calculate the arc length from (0, 60) to (60, 0) on the circle. The angle subtended by this arc at the center of the circle can be calculated as follows:
1. The initial position (0, 60) corresponds to an angle of π2 radians.
2. The final position (60, 0) corresponds to an angle of 0 radians.
3. The angle subtended is π2−0=π2 radians.
The arc length sA can be calculated using the formula:
sA=rθ
where r=60 m and θ=π2:
sA=60⋅π2=30π meters
Step 3: Calculate the time taken by particle A to reach (60, 0)
Using the speed of particle A, we can find the time TA it takes to travel this distance:
TA=sAvA=30π6π=5 seconds
Step 4: Determine the distance particle B needs to travel
Particle B starts at (0, 60) and needs to reach (60, 0). The distance sB can be calculated using the Pythagorean theorem:
sB=√(60−0)2+(0−60)2=√602+602=√3600+3600=√7200=60√2 meters
Step 5: Calculate the velocity of particle B
Since the collision occurs at the same time TB=TA, we can calculate the velocity vB of particle B:
vB=sBTB=60√25=12√2 m/s
Step 6: Determine the direction of particle B's velocity
To find the components of the velocity of particle B, we can use the direction of the displacement vector from (0, 60) to (60, 0):
- The change in x is 60−0=60.
- The change in y is 0−60=−60.
The velocity components can be calculated as follows:
vBx=6060√2⋅vB=6060√2⋅12√2=12 m/s
vBy=−6060√2⋅vB=−6060√2⋅12√2=−12 m/s
Final Answer
Thus, the velocity of particle B is:
→vB=12^i−12^j m/s
Particle A moves on a circle defined by the equation x2+y2=3600. The radius of this circle is 60 meters (since 602=3600). Particle A starts at the point (0, 60) and moves with a speed of 6π m/s.
To find the distance that particle A travels to reach the point (60, 0), we need to calculate the arc length from (0, 60) to (60, 0) on the circle. The angle subtended by this arc at the center of the circle can be calculated as follows:
2. The final position (60, 0) corresponds to an angle of 0 radians.
3. The angle subtended is π2−0=π2 radians.
sA=rθ
where r=60 m and θ=π2:
sA=60⋅π2=30π meters
Using the speed of particle A, we can find the time TA it takes to travel this distance:
TA=sAvA=30π6π=5 seconds
Particle B starts at (0, 60) and needs to reach (60, 0). The distance sB can be calculated using the Pythagorean theorem:
sB=√(60−0)2+(0−60)2=√602+602=√3600+3600=√7200=60√2 meters
Since the collision occurs at the same time TB=TA, we can calculate the velocity vB of particle B:
vB=sBTB=60√25=12√2 m/s
To find the components of the velocity of particle B, we can use the direction of the displacement vector from (0, 60) to (60, 0):
- The change in x is 60−0=60.
- The change in y is 0−60=−60.
vBx=6060√2⋅vB=6060√2⋅12√2=12 m/s
vBy=−6060√2⋅vB=−6060√2⋅12√2=−12 m/s
Thus, the velocity of particle B is:
→vB=12^i−12^j m/s
Topper's Solved these Questions
Similar Questions
Two particles move with constant velocities towards point O along straight lines in a plane as shown. The shortest distance A and B is

View SolutionTwo particles A and B are located at point (0m,50m) at t=0. The particle A moves withy a constant velocity and the particle B moves on a circle of radius 50 m having centre at origin (0,0) as shown in figure. The pasrticle B has a constant speed 5πm/s. What will be the velocity of particle A so that both the pasrticles reach at point (50m,0m) simultaneously.
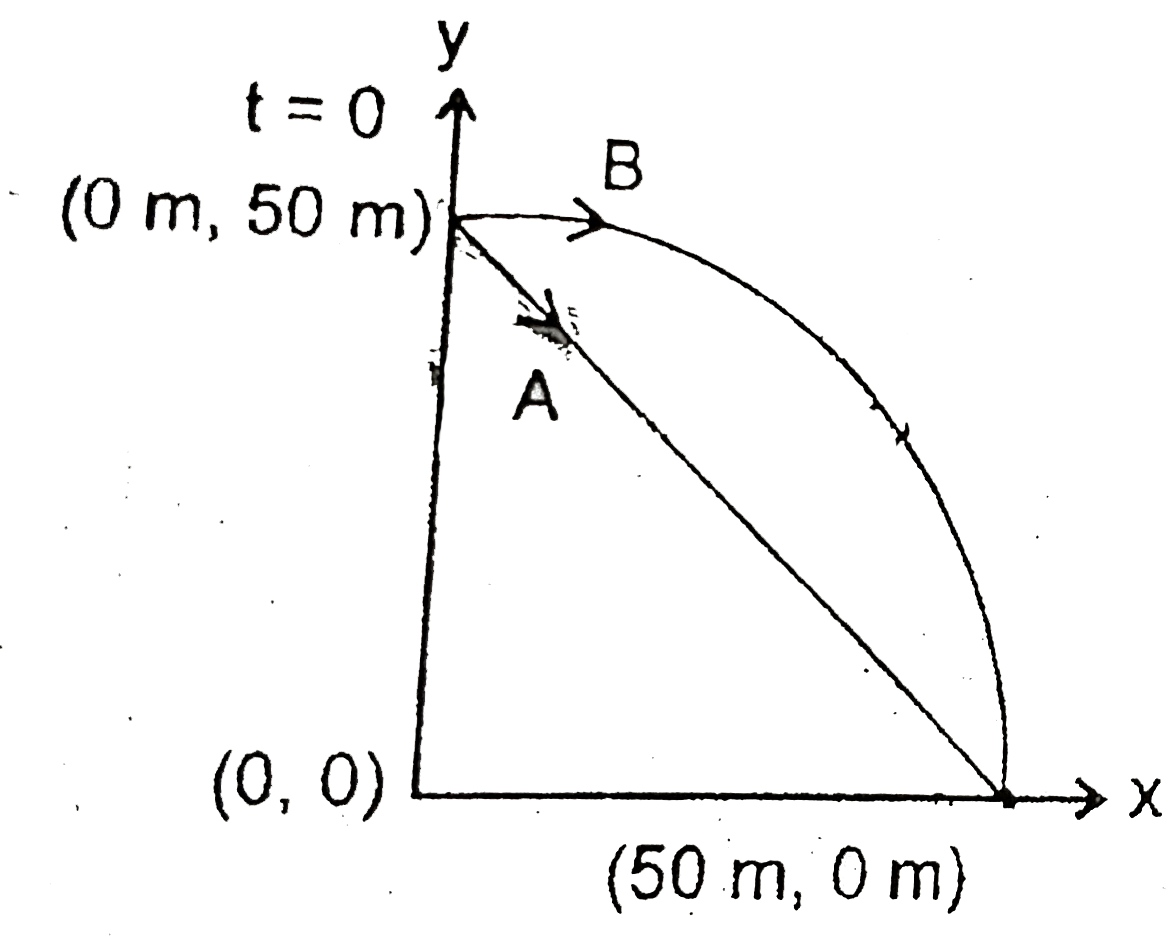
View Solution
Knowledge Check
A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
Two particles AandB move on a circle Initially, particles AandB are diagonally opposite to each other. Particle A moves with angular velocity πrads−1 and angular acceleration π/2rads−2 and particle B moves with constant angular velocity 2πrads−2. Find the time after which both the particlsd AnadB will collide.
View SolutionTwo particles A and B are located in x−y plane at points (0,0) and (0,4m). They simultaneoulsy start moving with velocities vA=2ˆjm/s and vB=2ˆim/s. Select the correct alternative(s)
View SolutionA car moving with constant acceleration crosses two points A and B with velocities 10 m/s and 20 m/s in its path. Find the velocity of the car midway between A and B. (in m/s).
View SolutionA particle moves in a circle of radius R=2122m with constant speed 1m/s. Find,
(a) magnitude of average velocity and
(b) magnitude of average acceleration in 2 s.
View SolutionA particle is moving along x-axis. The position of the particle at any instant is given by x=a+bt2 where ,a= 6 m and b= 3.5 ms−2 't' is measured in second .Find
(i) the velocity of the particle at 1s and
(ii) the average velocity between 3s and 6s
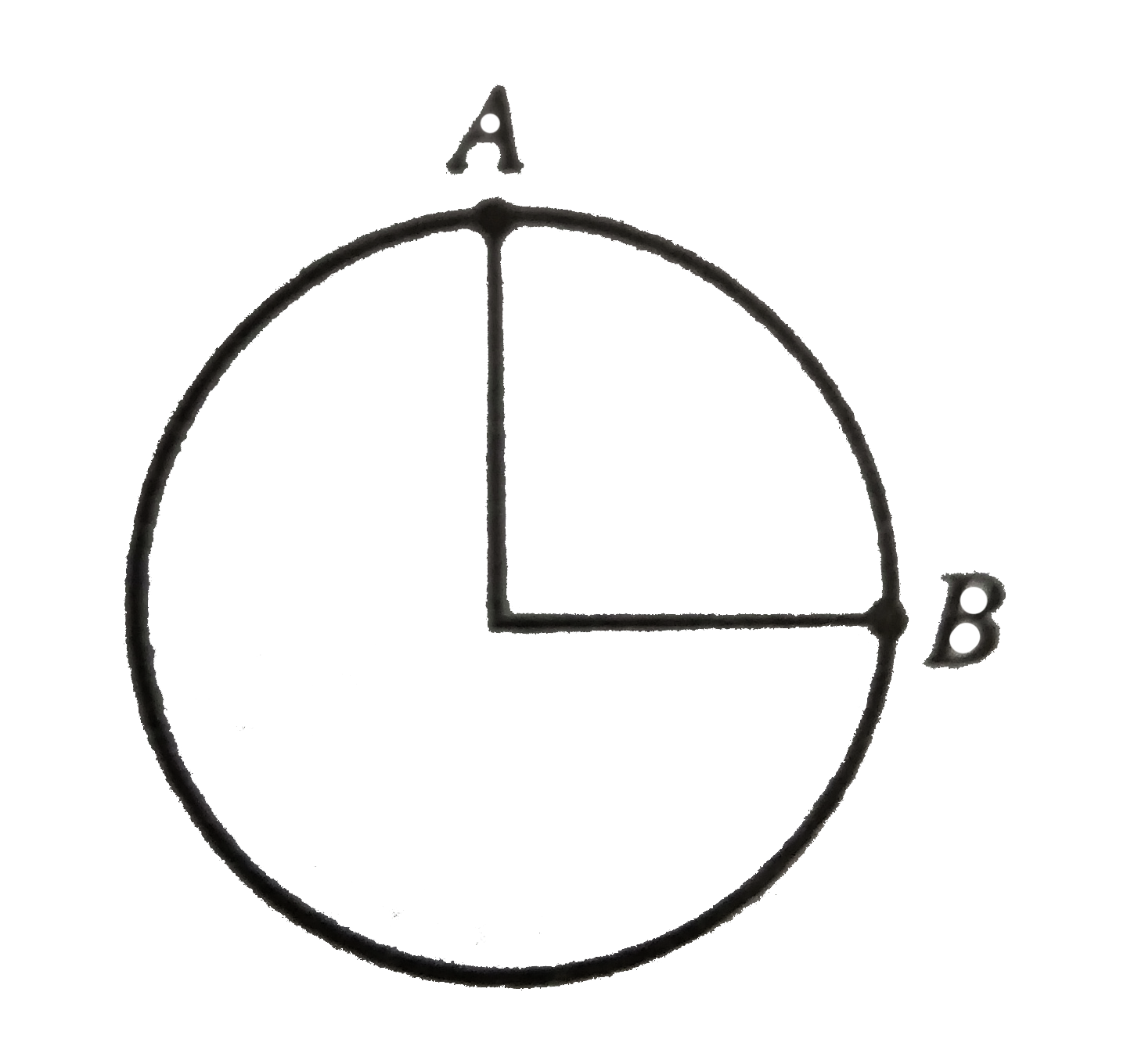
View SolutionA particle is moving in a circular path of radius 1 m. under the action of a centripetal force, the speed √2πms−1 of the particle is constant. Find the average of the velocity (inms−1) between A and B.
View SolutionTwo particles A and B are moving in XY plane. Particle A moves along a line with equation y=x while B moves along X axis such that their X coordinates are always equal. If B moves with a uniform speed 3 m/s the speed of A is
View Solution

