One end of the pile of chain falls vertically through a hole in its support and pull the remaining links steadily. The links which are at rest acquire the velocity of the hanging position suddenly and without loving interaction with the remaining stationery links and with the support. If the acceleration a of the falling chain is g/k. Find k. Ignore any friction.

Let the velocity of the end of the falling chain be v0 when a length x has already fallen. Taking mass per unit length of the chain as λ, we can write,
λxg−(λvdt)vdt=λx⋅vdvdx
gx−v2=xvdxdx
or vdvdx+v2x=g
This equation may be solved by using Intergrating factor. The solution is
v2=2gx3+Cx2. where C is an arbitary constant.
At t=0, x=0 and v=0
∴C=0 and v2=2gx3
Similar Questions
A uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
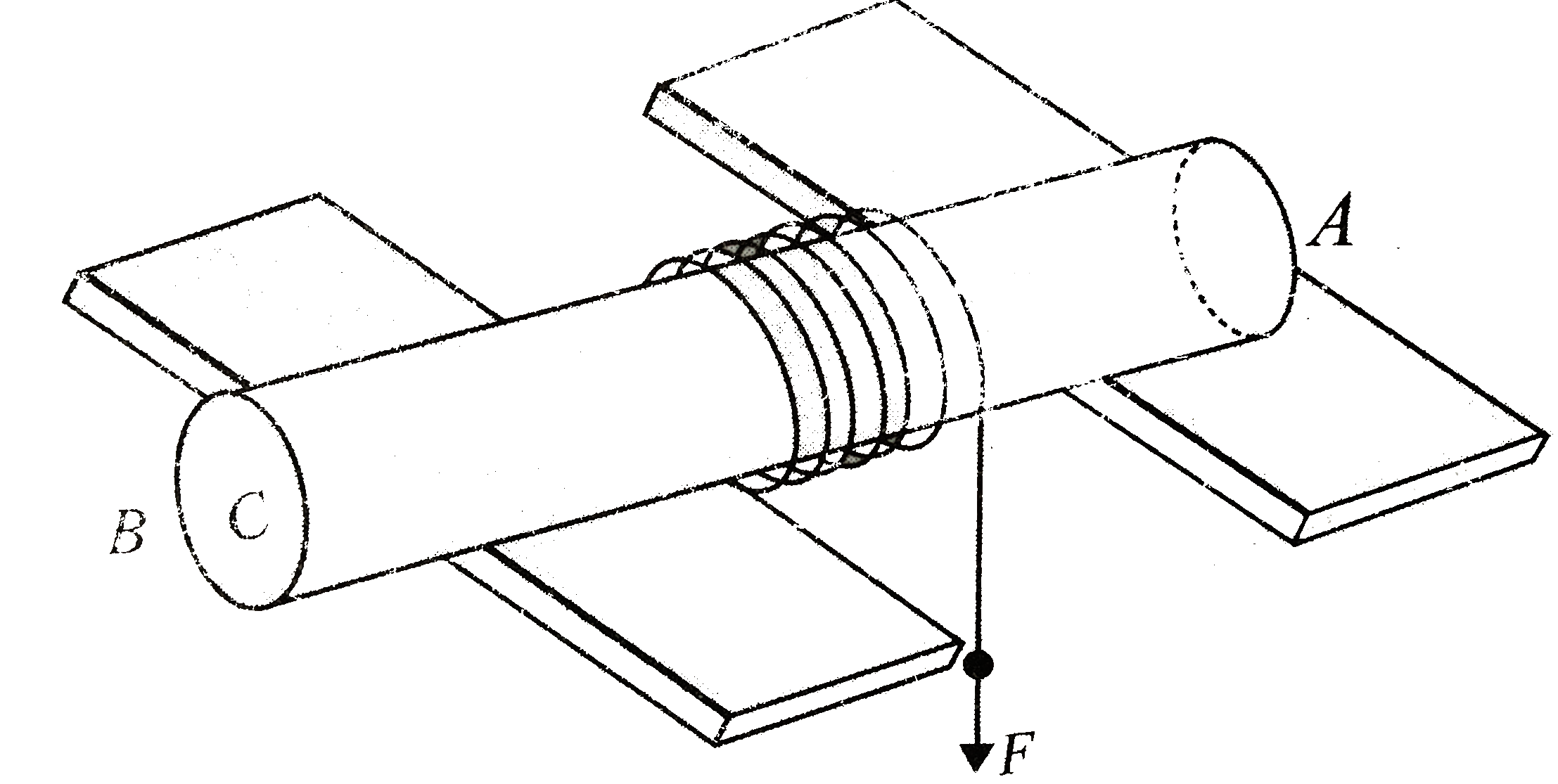
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?
View SolutionA very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
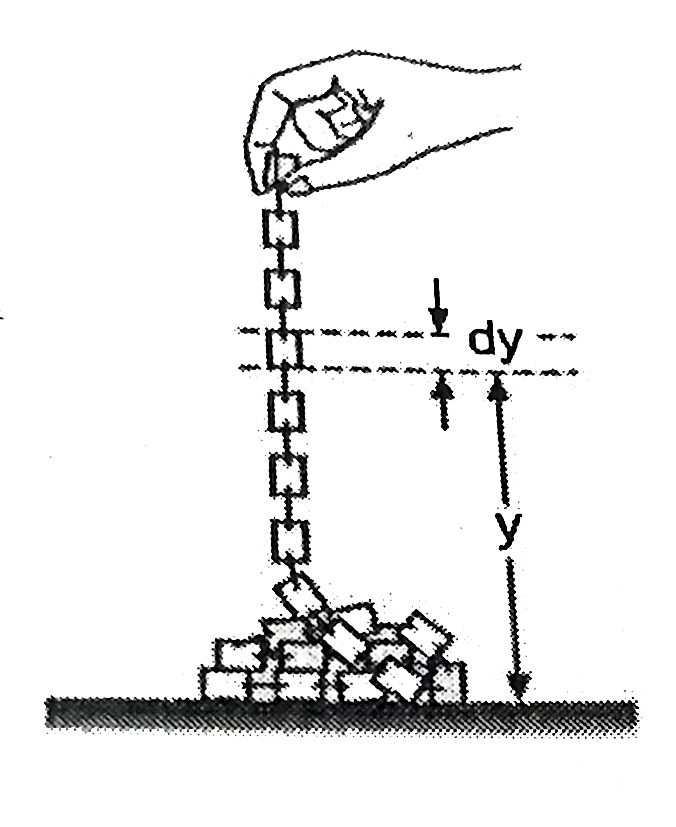
View SolutionA student tries to raise a chain consisting of three identical links. Each link has a mass of 300g. The three-piece chain is connected to a string and then suspended vertically, with the student holding the upper end of the string and pulling upward. Because of the student's pull, an upward force of 12 N is applied to the chain by the string.
(a) Draw a free-body diagram for each of the links in the chain and also for the entire-chain considered a single body.
(b) Use the results of part(a) Newton's laws to find (i) the acceleration of the chain and (ii) the force exerted by the top link on the middle link.
View SolutionThe flexible bicycle type chain of length πr2 and mass per unit length ρ is released from rest with θ=0∘ In the smooth circular channel and falls through the hole in the supporting surface, Determine the velocity v of the chain as the last link leaves the slot.
 .
.
View SolutionOne end a light spring of natural length d and spring constant k(=mg/d) is fixed on a rigid support and the other end is fixed to a smoth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the support. Initially , the spring makes an angle of 37∘ with the horizontal as shown in the figure. The system is released from rest. The speed of the ring at the same angle subtended downward will be
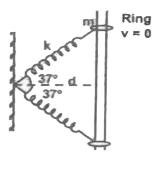
View SolutionA light rod length L, is hanging from the vertical smooth wall of a vehicle moving with acceleration √3g having a small mass attached at its one end is free to rotate about an axis passing through the other end. The minimum velocity given to the mass at its equilibrium position with respect to vehicle so that it can complete vertical circular motion respect to vehical) is √KgL. Find the value of K.
View SolutionA string is wrapped several times on a cylinder of mass M and radius R. the cylinder is pivoted about its adxis of block symmetry. A block of mass m tied to the string rest on a support positioned so that the string has no slack. The block is carefully lifted vertically a distance h, and the support is removed as shown figure.
a. just before the string becomes taut evalute the angular velocity ω0 of the cylinder ,the speed v0 of the falling body, m and the kinetic energy K0 of the system.
b. Evaluate the corresponding quanitities ω1,v1 and K1 for the instant just after the string becomes taut.
c. Why is K1 less than K0? Where does the energy go?
d. If M=m, what fraction of the kinetic energy is lost when the string becomes taut?
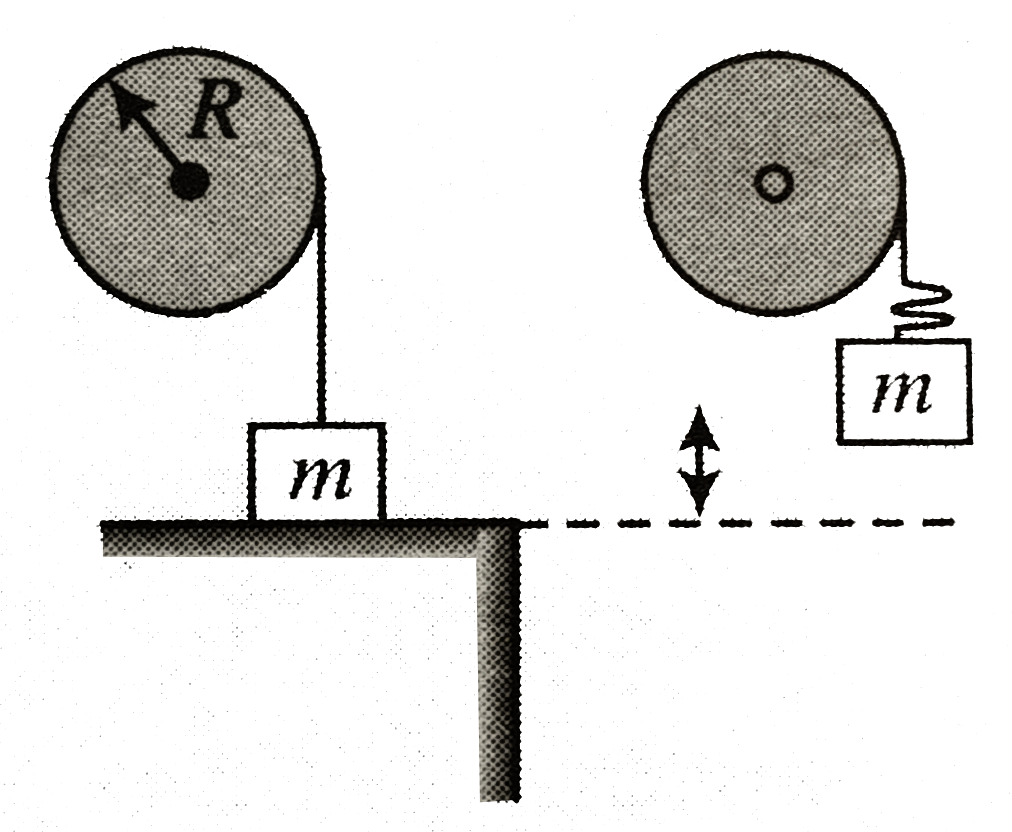
View SolutionIn the figure (i) a disc of mass M(kg) and radius R(m) is rotating smoothly about a fixed vertical axis AB with angular speed 26rad/s A rod rod CD of length R2(m) and mass M(kg) is hinged at one end at point 'D' on the disc. The rod remains in vertical position and rotates along with the disc about axis AB. At some moment the rod CD gets a very smal impulse at point 'C' due to air due to which the rod falls on the disc along one radius and sticks to the disc as shown in figure (ii). Now find the angular velocity of the disc in rad/s.

View Solution