A student tries to raise a chain consisting of three identical links. Each link has a mass of 300g. The three-piece chain is connected to a string and then suspended vertically, with the student holding the upper end of the string and pulling upward. Because of the student's pull, an upward force of 12 N is applied to the chain by the string.
(a) Draw a free-body diagram for each of the links in the chain and also for the entire-chain considered a single body.
(b) Use the results of part(a) Newton's laws to find (i) the acceleration of the chain and (ii) the force exerted by the top link on the middle link.
The correct Answer is:103ms−2:8N
To solve the problem step-by-step, we will first address part (a) by drawing the free-body diagrams for each link and the entire chain. Then, we will use Newton's laws to find the acceleration of the chain and the force exerted by the top link on the middle link as required in part (b).
Part (a): Free-Body Diagrams
1. Free-Body Diagram for the Entire Chain:
- The entire chain consists of three links, each with a mass of 300 g (0.3 kg).
- The total mass of the chain is 3×0.3kg=0.9kg.
- The weight of the chain (downward force) is given by W=mg=0.9kg×10m/s2=9N.
- The upward force applied by the student is F=12N.
- The free-body diagram will show:
- An upward force of 12 N.
- A downward force of 9 N (weight of the chain).
- The net force acting on the chain is Fnet=F−W=12N−9N=3N.
2. Free-Body Diagram for the Top Link:
- The top link has a weight of W1=mg=0.3kg×10m/s2=3N.
- The forces acting on it are:
- An upward force of 12 N (from the string).
- A downward force of 3 N (its own weight).
- An upward tension T1 from the middle link.
- The equation of motion for the top link can be written as:
Fnet=F−W1−T1=0.3a
3. Free-Body Diagram for the Middle Link:
- The middle link also has a weight of 3 N.
- The forces acting on it are:
- An upward tension T1 from the top link.
- A downward tension T2 to the bottom link.
- The equation of motion for the middle link can be written as:
T1−W1−T2=0.3a
4. Free-Body Diagram for the Bottom Link:
- The bottom link has a weight of 3 N.
- The forces acting on it are:
- An upward tension T2 from the middle link.
- The equation of motion for the bottom link can be written as:
T2−W1=0.3a
Part (b): Using Newton's Laws
(i) Finding the Acceleration of the Chain:
- From the free-body diagram of the entire chain, we can use Newton's second law:
Fnet=ma
3N=0.9kg×a
a=3N0.9kg=103m/s2≈3.33m/s2
(ii) Finding the Force Exerted by the Top Link on the Middle Link (Tension T1):
- Using the free-body diagram of the top link:
12N−T1−3N=0.3×103
12−T1−3=1⟹9−T1=1⟹T1=8N
Summary of Answers:
- (i) The acceleration of the chain is 103m/s2.
- (ii) The force exerted by the top link on the middle link is 8N.
- The entire chain consists of three links, each with a mass of 300 g (0.3 kg).
- The total mass of the chain is 3×0.3kg=0.9kg.
- The weight of the chain (downward force) is given by W=mg=0.9kg×10m/s2=9N.
- The upward force applied by the student is F=12N.
- The free-body diagram will show:
- An upward force of 12 N.
- A downward force of 9 N (weight of the chain).
- The net force acting on the chain is Fnet=F−W=12N−9N=3N.
- The top link has a weight of W1=mg=0.3kg×10m/s2=3N.
- The forces acting on it are:
- An upward force of 12 N (from the string).
- A downward force of 3 N (its own weight).
- An upward tension T1 from the middle link.
- The equation of motion for the top link can be written as:
Fnet=F−W1−T1=0.3a
- The middle link also has a weight of 3 N.
- The forces acting on it are:
- An upward tension T1 from the top link.
- A downward tension T2 to the bottom link.
- The equation of motion for the middle link can be written as:
T1−W1−T2=0.3a
- The bottom link has a weight of 3 N.
- The forces acting on it are:
- An upward tension T2 from the middle link.
- The equation of motion for the bottom link can be written as:
T2−W1=0.3a
- From the free-body diagram of the entire chain, we can use Newton's second law:
Fnet=ma
3N=0.9kg×a
a=3N0.9kg=103m/s2≈3.33m/s2
- Using the free-body diagram of the top link:
12N−T1−3N=0.3×103
12−T1−3=1⟹9−T1=1⟹T1=8N
- (i) The acceleration of the chain is 103m/s2.
- (ii) The force exerted by the top link on the middle link is 8N.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Single Correct
75 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.4
13 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Video
Similar Questions
A chain consisting of five links each with mass
View SolutionDraw the free body diagram of following also find the tension in each string
View SolutionA blocked of mass m is attached with two strings as shown in figure .Draw the free body diagram of the block.

View SolutionA block of mass m is attached with two strings as shown in figure .Draw the free body diagram of the block.

View SolutionA perfectly elastic uniform string is suspended vertically with its upper end fixed to the ceiling and the lower end loaded with the weight. If a transverse wave is imparted to the lower end of the string, the pulse will
View SolutionA block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a, find the force applied by the string and by the table N on the block.

View SolutionA man pulls out a block of mass m from the depth d with help of a light string. If acceleration of the block is g2 then the work done by the string on the block will be
View SolutionThe light and heavy chains is an antibody molecule are linked to each other mainly by
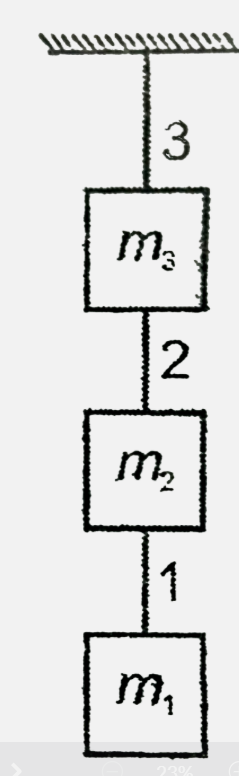
View SolutionFigure shows a three blocks are connected by strings. Its free body diagrams and find forces of interaction
View SolutionThe acceleration of the 2 kg block if the free end of string is pulled with a force of 20 N as shown is
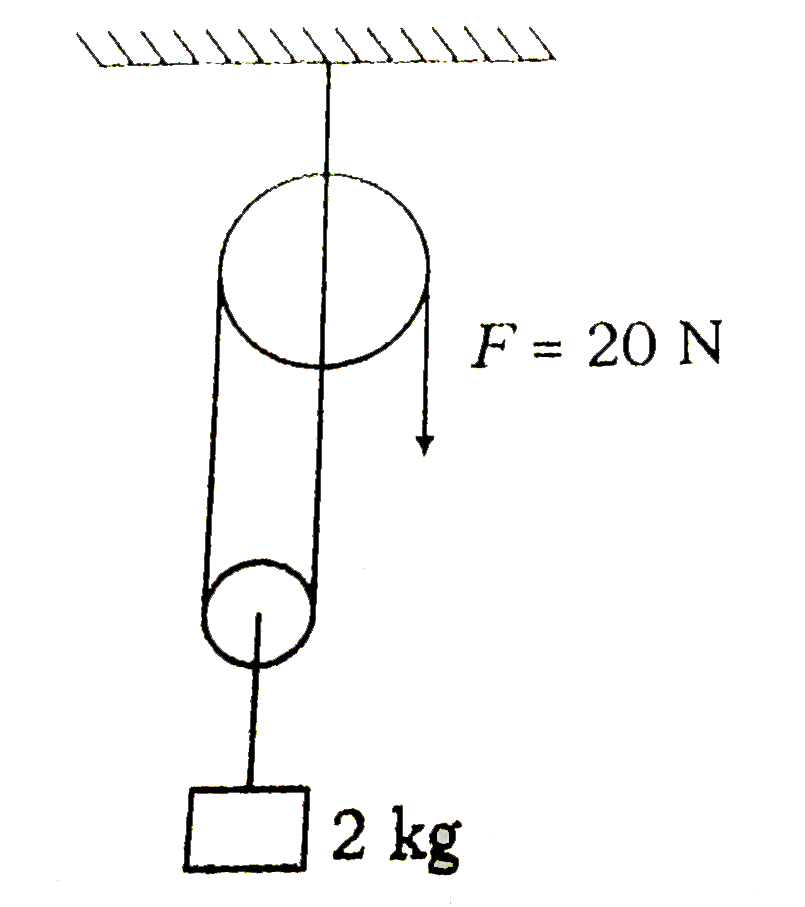
View Solution
