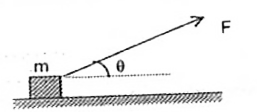
A block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a, find the force applied by the string and by the table N on the block.

Let us consider the block as the system.
The forces on the block are
a. pull of the earth, Mg, vertically downward,
b. contact force by the table , vertically upward,
c. pull of the string T, along the string.
The free body diagram for the block is shown in figure.
The acceleration of the block is horizontal and towards the right. Take this direction as the X-axis and vertically upward direction as the Y-axis. We have,

component of Mg along the X-axis =0
Component of N along the X-axis =0
component of T along the X-axis = T cosθ
Hence the total force along the X-axis = Tcosθ
Using Newton's law, Tcosθ=Ma......(i)
Component of Mg along the Y-axis =-Mg
Component of N along the Y-axis =N
Component of T along the Y-axis =Tsinθ
Total force along the Y-axis =N+Tsinθ−Mg
Using Newton's law N+Tsinθ−Mg=0 ...........(ii)
From equation (i), T=Macosθ. Putting this in equation ii. N=(Mg−Matanθ)
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - worked out Examples
11 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -1
14 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions
64 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
Similar Questions
A block of mass m is placed on a horizontla surface. If the block is pulled by applying a force of magnitude F=5mg at an angle θ=37∘, with horizontal as shown in fig. find the acceleration of the block at the given instant.

View SolutionA block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
View SolutionA force P acts on a smooth block of mass m placed on a horizontal floor at an angle θ with with horizontal on the block

View SolutionA block of mass m = 10 kg is pulled by a force F = 100 N at an angle θ=30∘ with the horizontal along a smooth horizontal surface. What is the acceleration of the block? (g=10m/s2)
View SolutionA block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surface is μ. If the block travels at a uniform velocity, find the work done by this applied force during a displacement d of the block.
View SolutionA block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surfasce is μ. If the block travels at a uniform velocity, find the work donen by this applied force during a displacement d of the blcok.
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point

View SolutionA block of mass M is being pulled with the help of a string of mass m and length L. the horizontal force applied by the man on the string is F.

Determine
(a) Find the force exerted by the string on the block and acceleration of system.
(b) Find the tension at the mid point of the string.
(c ) Find the tension at a distance x from the end at which force is applied.
Assume that the block is kept on a frictionless horizontal surface and the mass is uniformly distributed in the string.
View Solution
