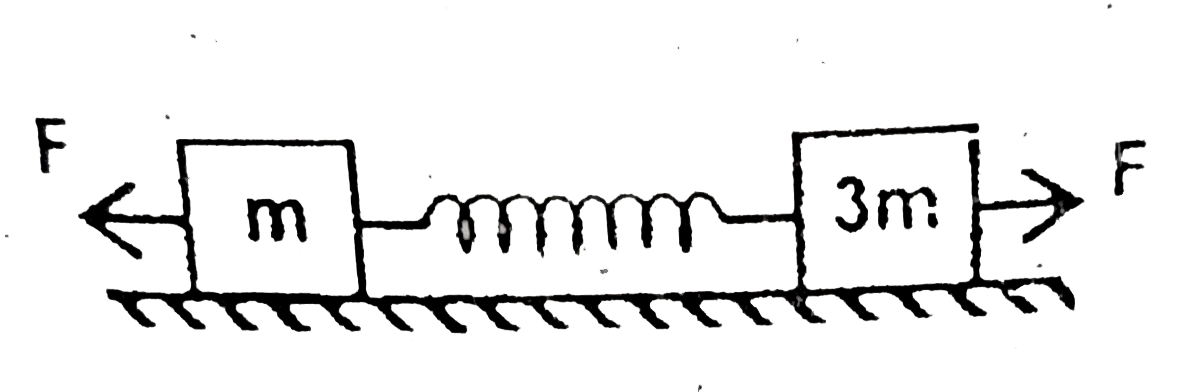
Three point masses m, 2m and m, connected with ideal spring (of spring constant k) and ideal string as shown in the figure, are placed on a smooth horizontal surface
At t=0, three constant forces F, 2F and 3F start acting on the point masses m, 2m and m respectively, as shown in figure. Find the maximum extension in the spring

2Fk
5F2k
3Fk
8F3k
Let any time t1 extension in spring is x, so
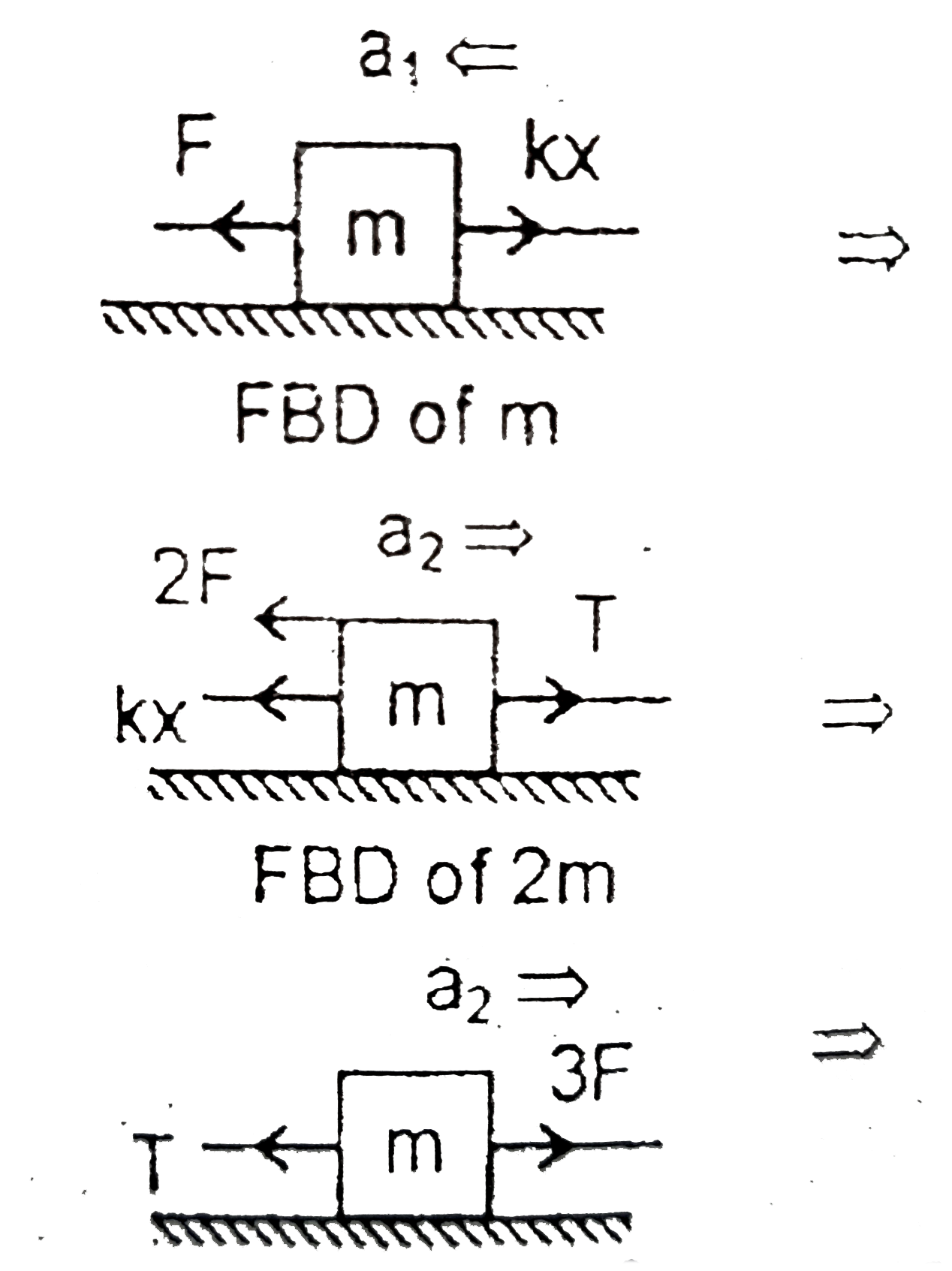 ⇒F−kx=ma1⇒a1=F−kxm….(1)
⇒F−kx=ma1⇒a1=F−kxm….(1)
 ⇒T−kx−2F=2ma2……(2)
⇒T−kx−2F=2ma2……(2)
 ⇒3F−T=ma2.....(3)
⇒3F−T=ma2.....(3)
With the help of equations (2) and (3), we have
F=kx=3ma2⇒F−kx3m=a2.......(4)
With the help of equations (1) and (4), we have
→a12=→a1−→a2=a1(−ˆi)−a2(ˆi)=(a1+a2)(ˆi)
V12dV12dx=a12=4(F−kx)3m⇒∫00V12dV12=43m∫x0(F−kx)dx
⇒0=43m[Fx−kx22]⇒Xmax=2Fk
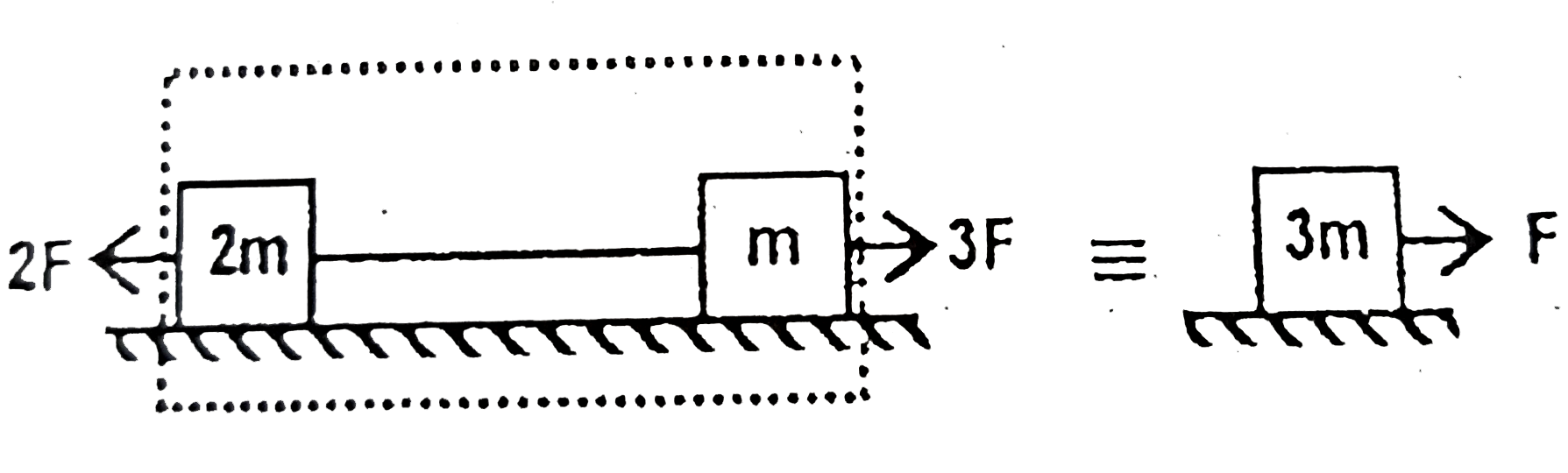
Second method : System is equivalent to
Because
Above system behaves as single unit
Similar Questions
A block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is upstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionTwo masses m1 and m2 are placed on a smooth horizontal surface and are connected by a string of negligible mass. A horizontal force F is applied on the mass m2 as shown in the figure. The tension in the string is

View SolutionThree identical cubes each of mass m are place on a smooth horizontal surface.A constant force F is applied on A as shown in the figure.The force on B applied by C is
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionTwo blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth plane .find the value of spring force .
View SolutionTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .
.
View SolutionTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .
.
View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
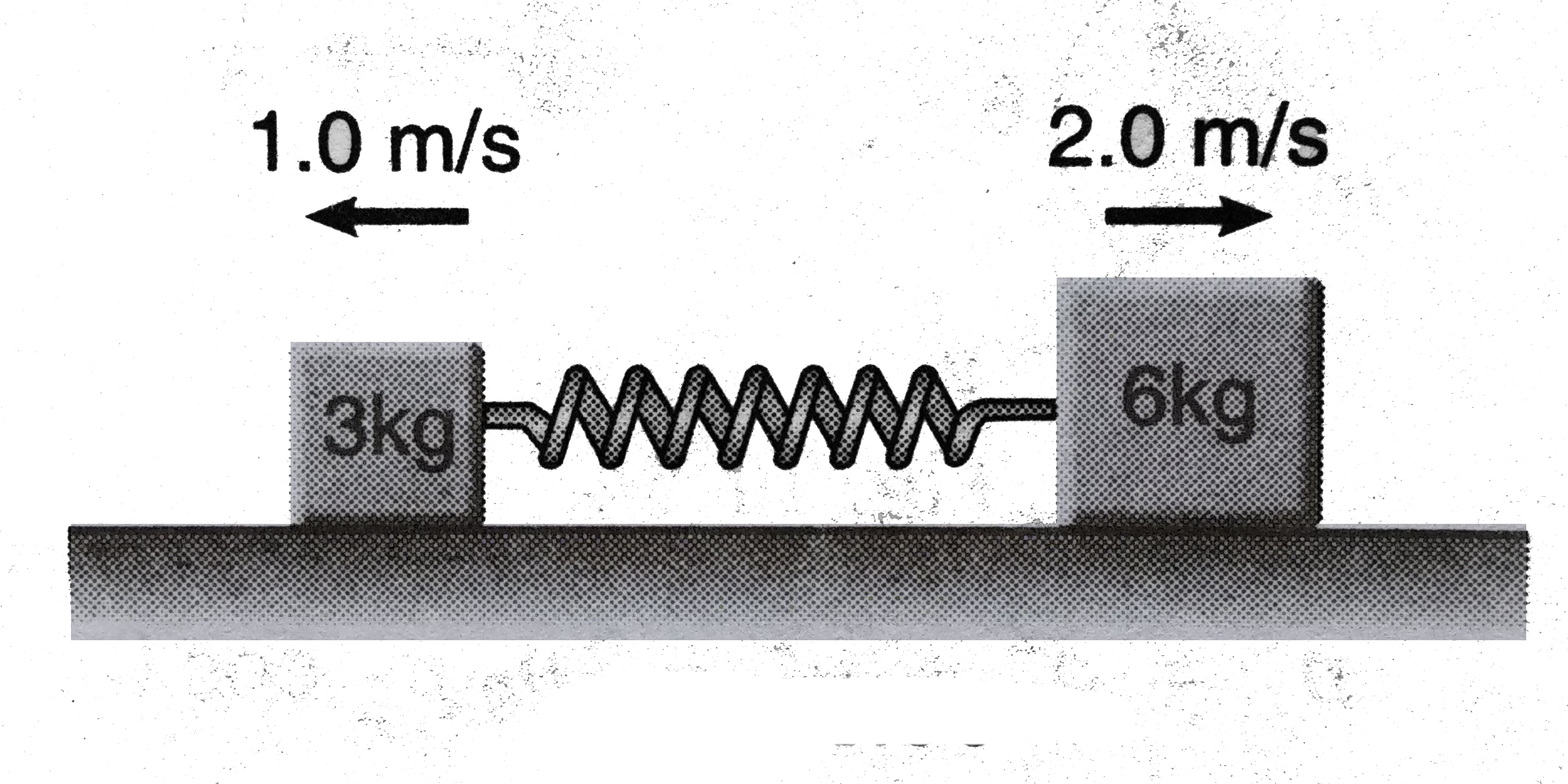
View Solution