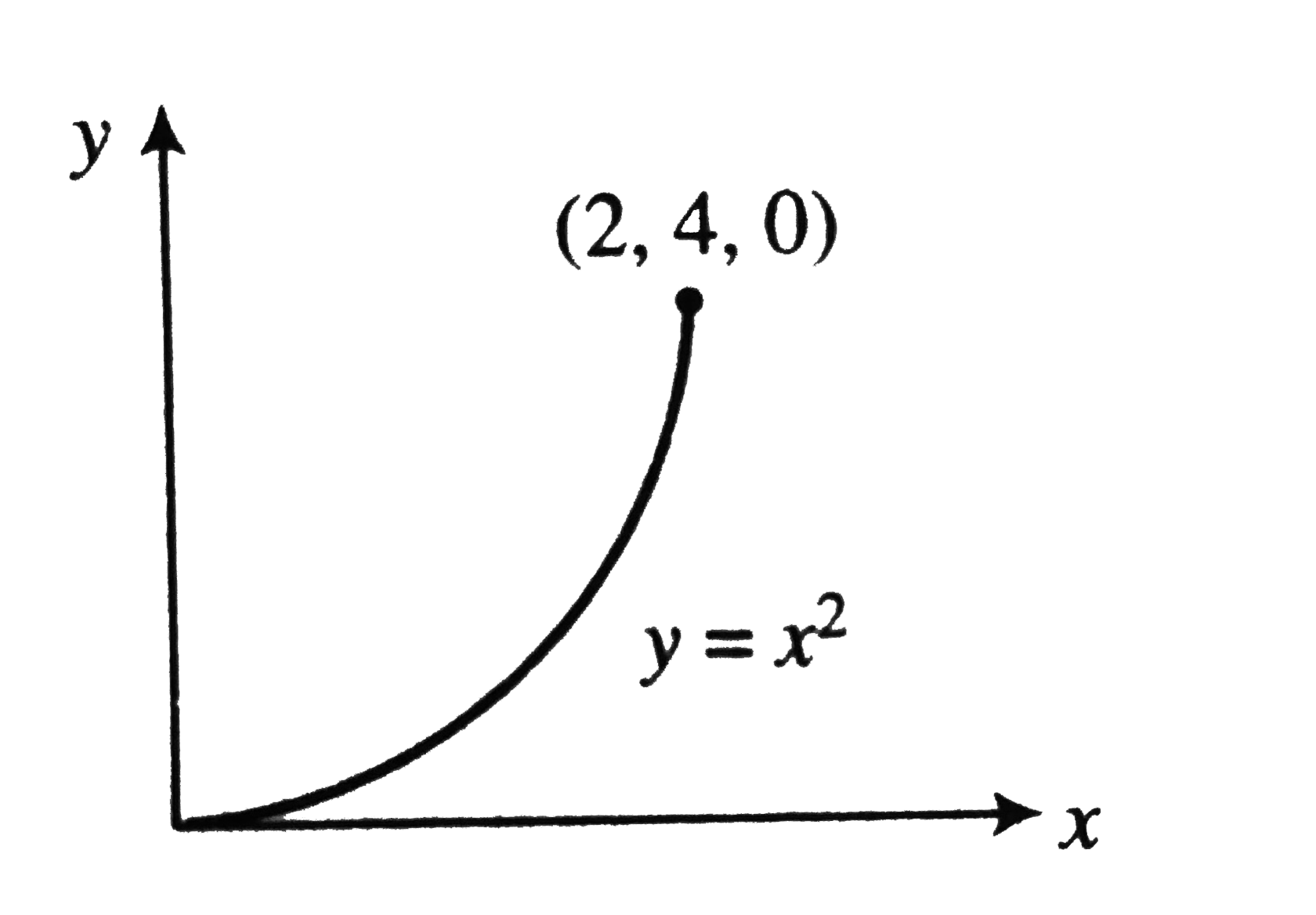
A force $\to F = (3 x y - 5 z) ˆ j + 4 z ˆ k$ is applied on a particle. The work done by the force when the particle moves from point $(0, 0, 0)$ to point $(2, 4, 0)$ as shown in figure.

$\frac{280}{5}$

$\frac{140}{5}$

$\frac{232}{5}$

$\frac{192}{5}$

Video Solution

Text Solution

Verified by Experts

The $z$ -component of the force and the $x$ -component of displacement are ieffective here.
$d W = F_{y} d y = 3 x y . d y$ ( $∵ z = 0$ )
$= 6 x^{4} d x$ ( $∵ y = x^{2}$ )
Integrating between $x = 0$ and $x = 2$ gives the result.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Knowledge Check

A force F is related to the position of a particle by the relation $F = (10 x^{2}) N$ . Find the work done by the force when the particle moves from $x = 2 m \to x = 4 m$ .
A $\frac{56}{3}$ J
B560 J
C $\frac{560}{3}$ J
D $\frac{3}{560}$ J

A force $\to F = (2 x ˆ i + 3 ˆ j + 3 z^{2} ˆ k)$ is acting on the particle of mass 2kg which is displaces from point $A (2, 3, 0)$ to point $B (3, 2, 1)$ . the work done by the force on the particle will be
View Solution
If force $F = (2 x + 3 x^{2}) N$ is applied on a particle along x = axis, then find the work done by it during motion of particle from x = 0 to x = 2 m.
View Solution
Shown that work done by a conservative force on a particle moving between two points is path independent.
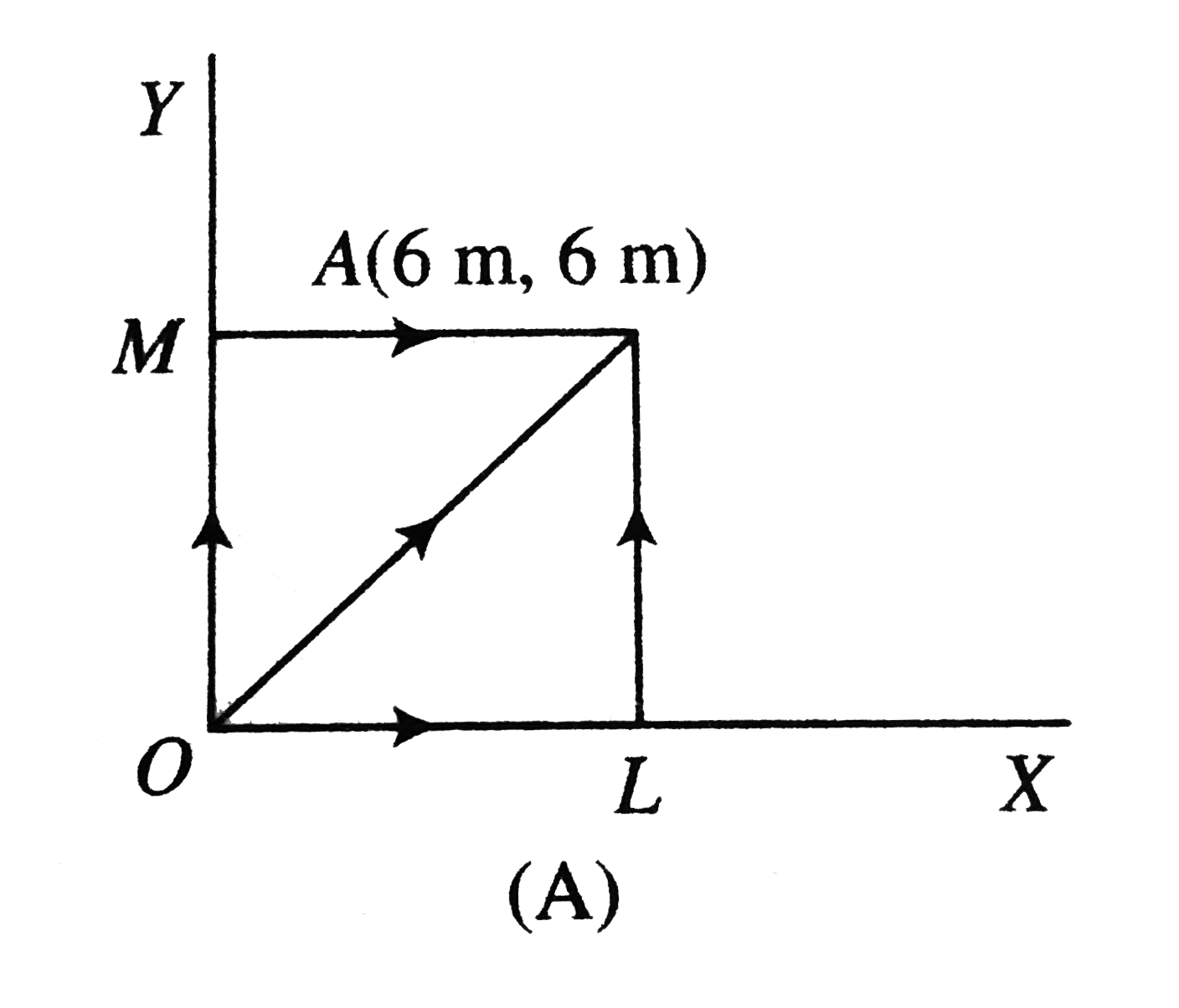
View Solution
Force acting on a particle moving in the x-y plane is $\to F = (y^{2} ˆ i + x ˆ j) N$ , x and y are in metre. As shown in figure, the particle moves from the origin O to point A $(6 m, 6 m)$ . The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
Now consider another situation. A force $\to F = (4 ˆ i + 3 ˆ j) N$ acts on a particle of mass $2 k g$ . The particle under the action of this force moves from the origin to a point A $(4 m, - 8 m)$ . Initial speed of the particle, i.e., its speed at the origin is $2 \sqrt{6} m s^{- 1}$ . Figure shows three paths for the motion of the particle from O to A.

Speed of the particle at A will be nearly
View Solution
Force acting on a particle moving in the x-y plane is $\to F = (y^{2} ˆ i + x ˆ j) N$ , x and y are in metre. As shown in figure, the particle moves from the origin O to point A $(6 m, 6 m)$ . The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
Now consider another situation. A force $\to F = (4 ˆ i + 3 ˆ j) N$ acts on a particle of mass $2 k g$ . The particle under the action of this force moves from the origin to a point A $(4 m, - 8 m)$ . Initial speed of the particle, i.e., its speed at the origin is $2 \sqrt{6} m s^{- 1}$ . Figure shows three paths for the motion of the particle from O to A.

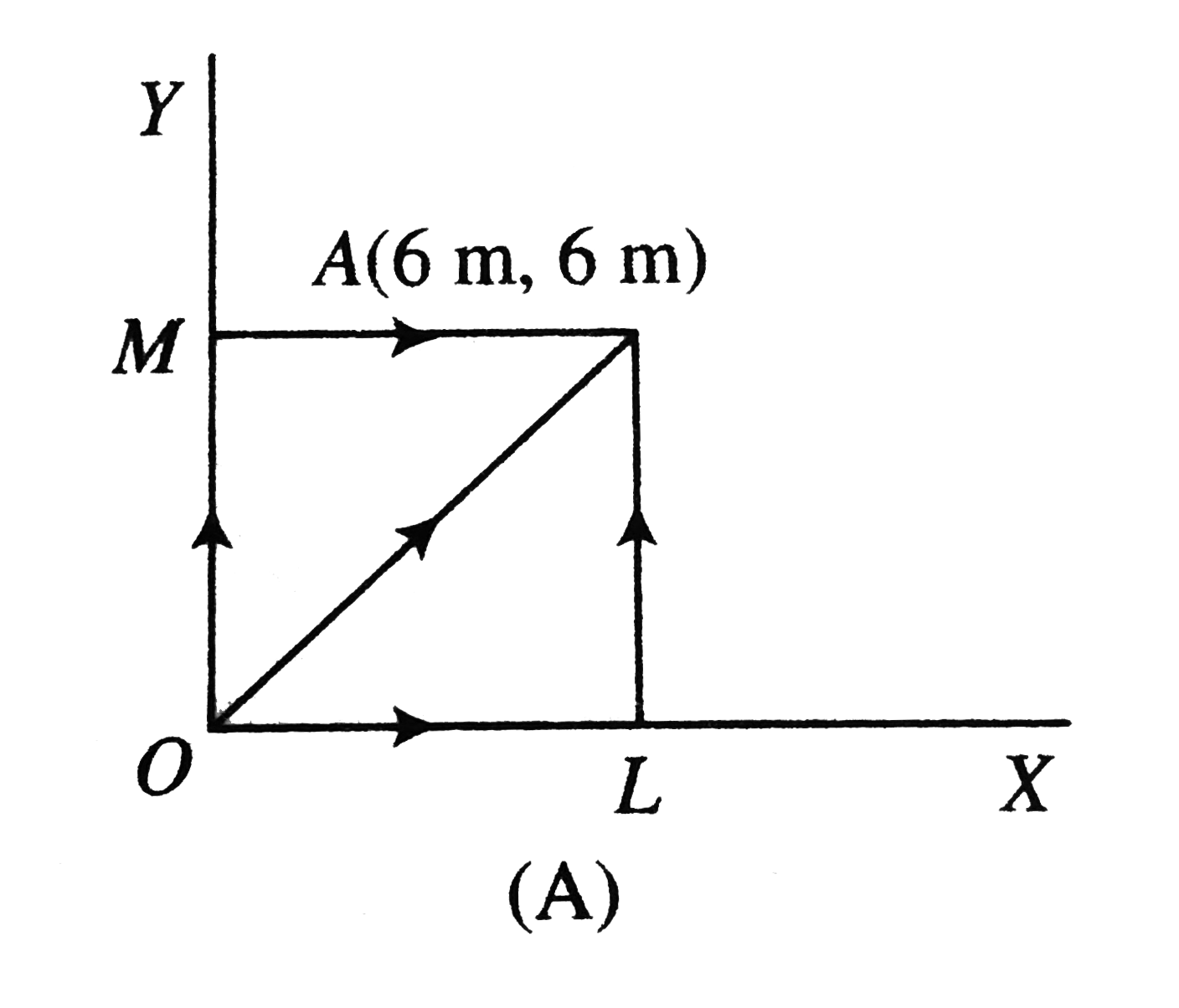
If the potential energy at O is $16 J$ , the potential energy at A will be
View Solution
A force bar F = (3hat i-4 hat j +b hat k)N is acting on the particle which is moving from point A ( 0-1, 1) m to the point B(2, 2 3) m If net work done by the force on the particle is zero then value of b is
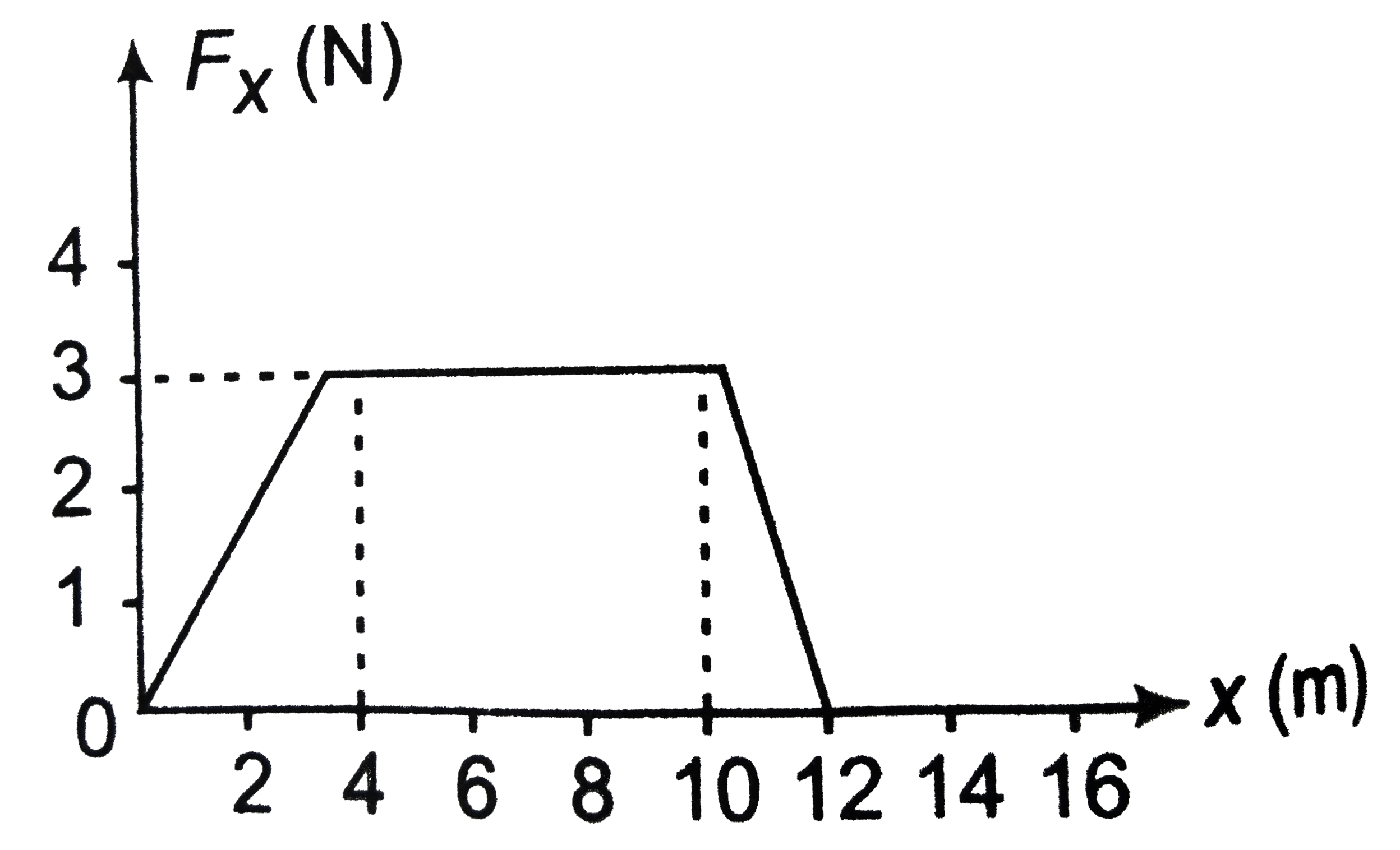
View Solution
A particle is subjected to a force $F_{x}$ that varies withes position as shown in figure. Find the work done by the force on the body as it moves
(a) from $x = 10.0 m$ to $x = 5.0 m$ ,
(b) from $x = 5.0 m$ to $x = 10.0 m$ ,
(c ) from $x = 10.0 m$ to $x = 15.0 m$ ,
(d) what is the total work done by the force over the distance $x = 0$ to $x = 15.0$ ?
.
View Solution

A force $\to F = (3 x y - 5 z) ˆ j + 4 z ˆ k$ is applied on a particle. The work done by the force when the particle moves from point $(0, 0, 0)$ to point $(2, 4, 0)$ as shown in figure.

The $z$ -component of the force and the $x$ -component of displacement are ieffective here.
$d W = F_{y} d y = 3 x y . d y$ ( $∵ z = 0$ )
$= 6 x^{4} d x$ ( $∵ y = x^{2}$ )
Integrating between $x = 0$ and $x = 2$ gives the result.

Similar Questions

Knowledge Check

A force F is related to the position of a particle by the relation $F = (10 x^{2}) N$ . Find the work done by the force when the particle moves from $x = 2 m \to x = 4 m$ .

Recommended Questions

A force →F=(3xy−5z)ˆj+4zˆk is applied on a particle. The work done by the force when the particle moves from point (0,0,0) to point (2,4,0) as shown in figure.

The z-component of the force and the x-component of displacement are ieffective here. dW=Fydy=3xy.dy (∵z=0) =6x4dx (∵y=x2 ) Integrating between x=0 and x=2 gives the result.

Similar Questions

Knowledge Check

A force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.

Recommended Questions

A force $\to F = (3 x y - 5 z) ˆ j + 4 z ˆ k$ is applied on a particle. The work done by the force when the particle moves from point $(0, 0, 0)$ to point $(2, 4, 0)$ as shown in figure.

The $z$ -component of the force and the $x$ -component of displacement are ieffective here.
$d W = F_{y} d y = 3 x y . d y$ ( $∵ z = 0$ )
$= 6 x^{4} d x$ ( $∵ y = x^{2}$ )
Integrating between $x = 0$ and $x = 2$ gives the result.

A force F is related to the position of a particle by the relation $F = (10 x^{2}) N$ . Find the work done by the force when the particle moves from $x = 2 m \to x = 4 m$ .