Choose the correct option:
In the arrangement shown in Fig. gas is thermally insulated. An ideal gas is filled in the cylinder having pressure P0 (gt atmospheric pressure Pa). The spring of force constant K is initially un-stretched. The piston of mass m and area S is frictionless. In equilibrium, the piston rises up by distance x0, then
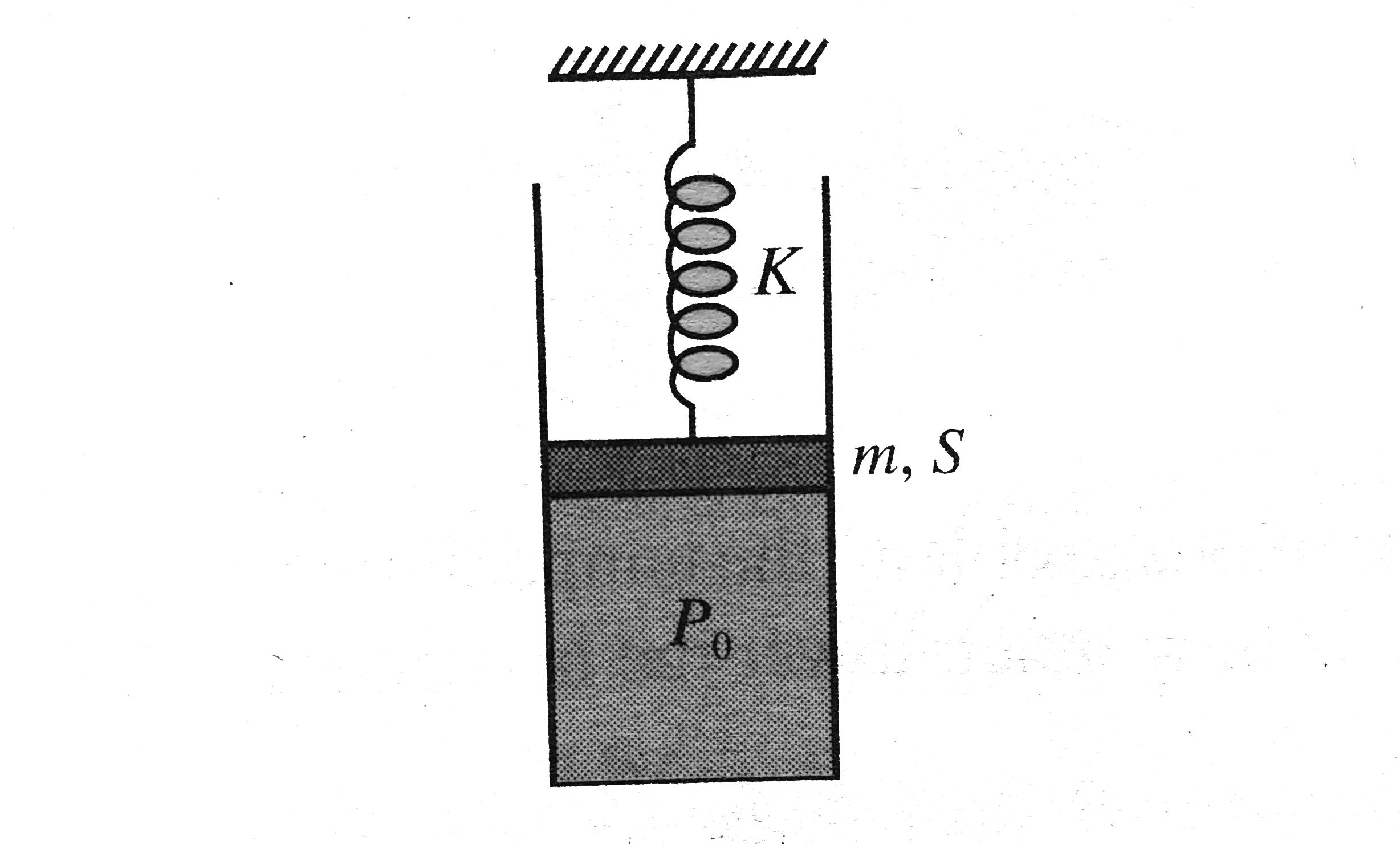
Final pressure of the gas is (P0+kx0S+mgS)
Work done by the gas is greater than (12kx20+mgx0)
Decrease in internal energy is (12kx20+mgx0+P0sx0)
none of these
In equilibrium, piston will be having kinetic energy, too.
Similar Questions
A thermally insulated chamber of volume 2V0 is divided by a frictionless piston of area S into two equal part A and B. Part A has an ideal gas at pressrue P0 and temperature T0 and part B is vacuum. A massless spring of force constant K is connected with the piston and the wall of the container as shown. Initially the spring is unstretched. The gas inside chamber A is allowed to expand. Let in equilibrium the spring be compressed by x0. Then

View SolutionA thermally insulated chamber of volume 2V0 is divided by a frictionless piston of area S into two equal part A and B. Part A has an ideal gas at pressrue P0 and temperature T0 and part B is vacuum. A massless spring of force constant K is connected with the piston and the wall of the container as shown. Initially the spring is unstretched. The gas inside chamber A is allowed to expand. Let in equilibrium the spring be compressed by x0. Then

View SolutionA fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at its bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
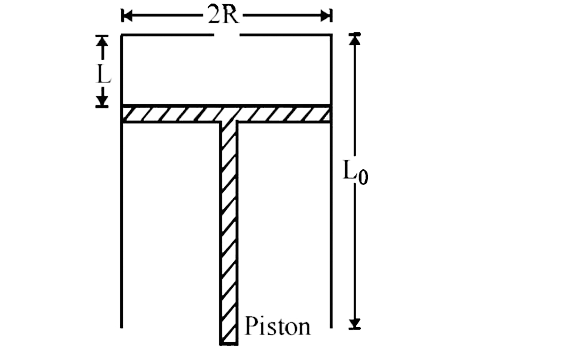
While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top is
View SolutionThe fixed non-conducting cylinder shown in figure has a noconducting heavy piston of mass M that can slide without friction. The area of piston is S and the cylinder is filled with an ideal gas (λ=1.5) with an initial volume V and an initial pressure P. Assume that the outside pressure on the piston is zero (vaccum). (Neglect acceleration due to gravity).
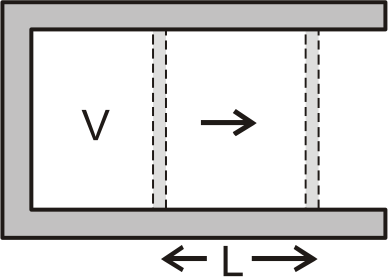
For the temperature of the gas to drop to one half of its original value. the piston will have to move by a distance:
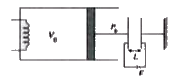
View SolutionAn ideal gas is enclosed in a cylinder fitted with a frictionless piston. The piston is connected with a light rod to one plate of capacitor whose other plate is fixed as shown. Initially volume of the gas inside the cylinder is V0 Atmospheric pressure is P0 separation between the plates is L, area of the piston as well as of the capacitor plates is A and emf of battery is ε . A heater supplies heat to the gas so that pressure of the gas is given as P=P0−nε0ε2L2 when piston is displaced by a distance L2 . Find value of n.
View SolutionFigure shows initial state of an ideal gas trapped in a container with conducting walls and a piston (mass m) which can move without any friction. The container is placed on point supports and its wall are conducting. Assuming that atmospheric pressure is P0 and the mass of the ideal gas is negligible as compared to the mass of the piston and the mass of container. Take the cross section area of piston to be A. The piston is slowly lifted by an external agent and held in its position. Let M be the maximum mass of container so that it may "lift off" while pulling the piston upwards and Pi be the pressure of ideal gas in initial state. Pick the correct choice:

View SolutionAn ideal monoatomic gas is confined in a horizontal cylinder by a spring loaded piston (as shown in the figure). Initially the gas is at temperature T1, pressure P1 and volume V1and the spring is in its relaxed state. The gas is then heated very slowly to temperature T2,pressure P2and volume V2. During this process the piston moves out by a distance x. Ignoring the friction between the piston and the cylinder, the correct statement (s) is (are)

View SolutionAn ideal monoatomic gas is confined in a cylinder by a spring-loaded piston of cross-section 8.0×10−3m2. Initially the gas is at 300K and occupies a volume of 2.4×10−3m3 and the spring is in its relaxed (unstretched, unompressed) state, fig. The gas is heated by a small electric heater until the piston moves out slowly by 0.1m. Calculate the final temperature of the gas and the heat supplied (in joules) by the heater. The force constant of the spring is 8000N/m, atmospheric pressure is 1.0×105Nm−2. The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible. Assume the spring to be massless.

View SolutionAn ideal monoatomic gas is confined in a cylinder by a spring-loaded piston of cross-section 8.0×10−3m2. Initially the gas is at 300K and occupies a volume of 2.4×10−3m3 and the spring is in its relaxed (unstretched, unompressed) state, fig. The gas is heated by a small electric heater until the piston moves out slowly by 0.1m. Calculate the final temperature of the gas and the heat supplied (in joules) by the heater. The force constant of the spring is 8000N/m, atmospheric pressure is 1.0×105Nm−2. The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible. Assume the spring to be massless.

View SolutionA weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V.2 moles of an ideal gas at pressure P=2 atmosphere are confined to the part with volume V=1 litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, γ=1.5.
View Solution
