A conducting ring of mass m and radius r has a weightless conducting rod PQ of length 2r and resistance 2R attached to it along its diametre. It is pivoted at its centre C with its plane vertical, and two blocks of mass m and 2m are suspended by means of a light inextensible string passing over it as shown in Fig. The ring is free to rotate about C and the system is placed in magnetic field B (into the plane of the ring). A circuit is now complete by connecting the ring at A and C to a battery of emf V. It is found that for certain value of V , the system remains static.

The value of V can be related with m, B and r as
Resistance of PQ=2R
Since equivalent resistance of the circuit is R/2, in static condition current through the battery is I=2V/R
The current through CP and CQ is i=I/2=V/R
Consider the FBD of ring and the blocks
Consider torque about 'C'
τN=0
τmg=0, τF2=Bir22(ˆk)
τT1=T1rˆk
τT2=T2r(−ˆk)
τf1=Bir22ˆk ltbr gt ∵τN+τmg+τF1+τF1=0
⇒T1r−T2r+Bir22+Bir22=0 .....(i)
As system is in static equilibrium
T1=mg.....(i)
and T2=2mg.....(ii)
Putting the values of T1 and T2 in equation (i)
mgr−2mgr+Bir2=0
⇒i=mgBr⇒VR=mgBr⇒V=mgBr
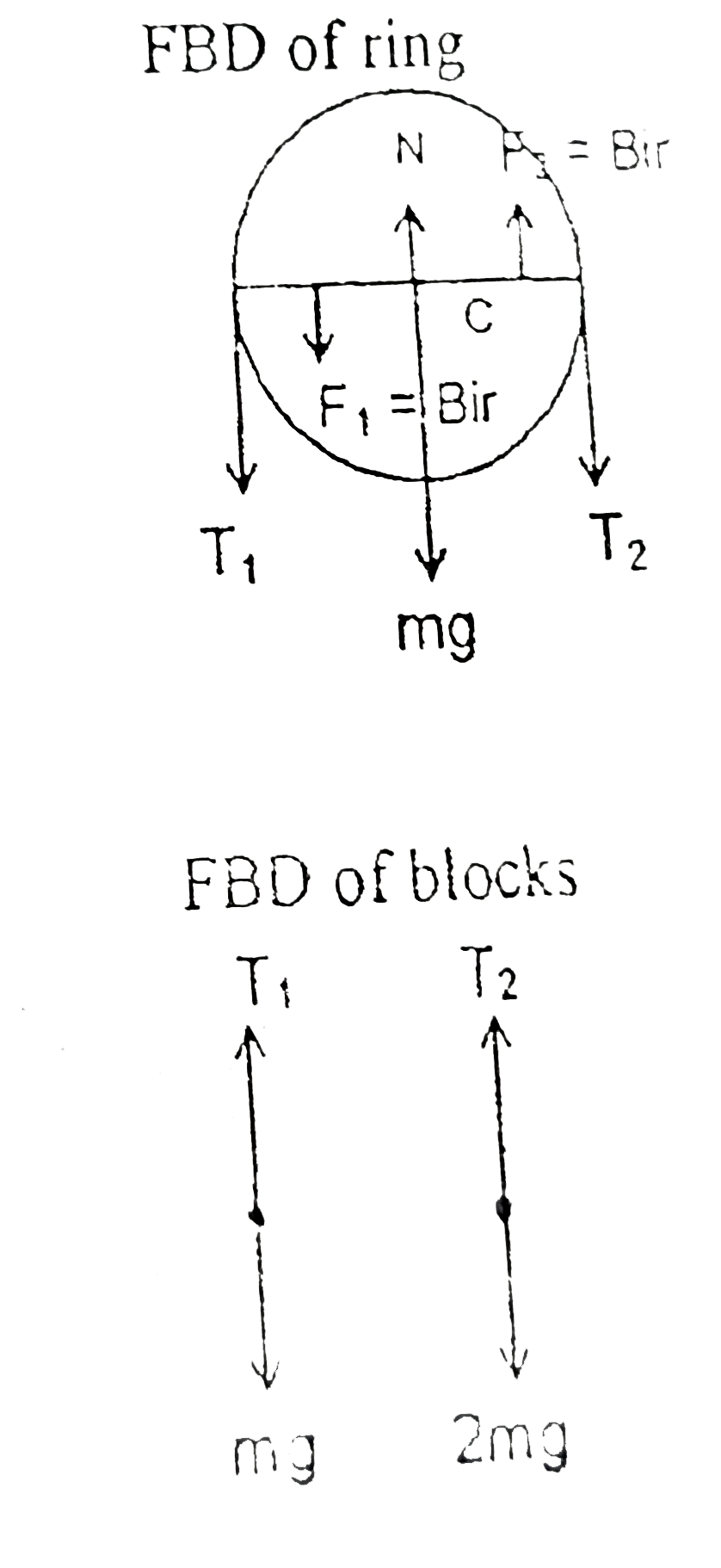
Similar Questions
A conducting ring of mass m and radius r has a weightless conducting rod PQ of length 2r and resistance 2R attached to it along its diametre. It is pivoted at its centre C with its plane vertical, and two blocks of mass m and 2m are suspended by means of a light inextensible string passing over it as shown in Fig. The ring is free to rotate about C and the system is placed in magnetic field B (into the plane of the ring). A circuit is now complete by connecting the ring at A and C to a battery of emf V. It is found that for certain value of V , the system remains static.

Net torque applied by the tension in strings can be related as
View SolutionA conducting ring of mass m and radius r has a weightless conducting rod PQ of length 2r and resistance 2R attached to it along its diametre. It is pivoted at its centre C with its plane vertical, and two blocks of mass m and 2m are suspended by means of a light inextensible string passing over it as shown in Fig. The ring is free to rotate about C and the system is placed in magnetic field B (into the plane of the ring). A circuit is now complete by connecting the ring at A and C to a battery of emf V. It is found that for certain value of V , the system remains static.

In static condition, find the current through rod PC.
View SolutionFor a uniform ring of mass M and radius R at its centre
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View Solutiontwo masses 2m and m are attached to the the ends of a string while passing over a smooth Pulley of mass m and radius R. The ratio of tensions in both the strings is
_PHY_E05_245_Q01.png)
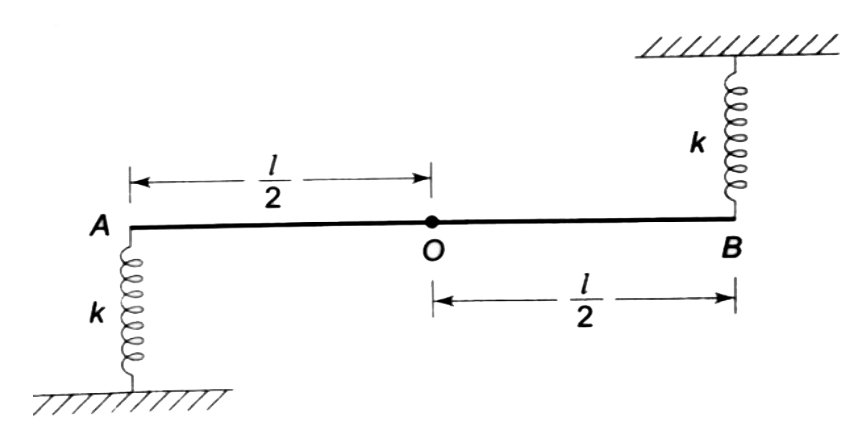
View SolutionThe ends of a rod of length l and mass m are attached to two identical springs as shown in the figure. The rod is free to rotate about its centre O . The rod is depressed slightly at end A and released . The time period of the oscillation is
View SolutionTwo point masses m1 and m2 are joined by a weightless rod of length r. Calculate the moment of inerrtia of the system about an axis passing through its centre of mass and perpendicular to the rod.
View Solution
