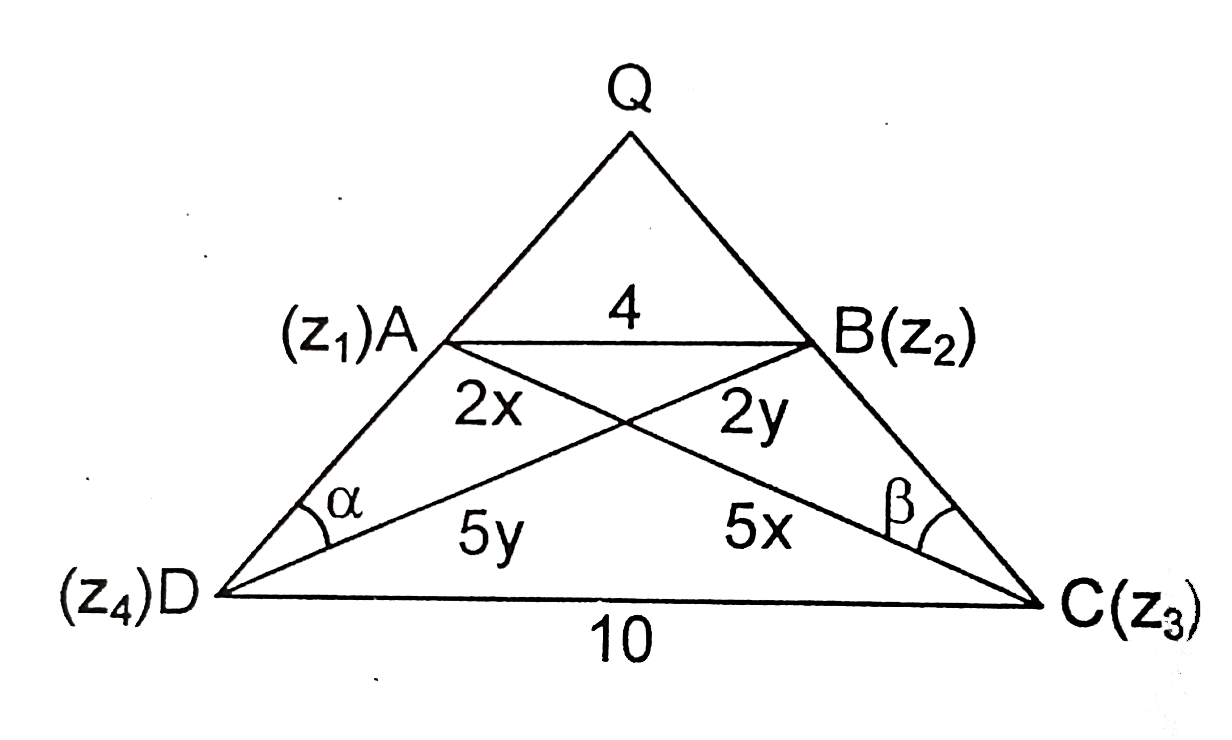
Let A(z1),B(z2),C(z3 and D(z4) be the vertices of a trepezium in an Argand plane such that AB∣∣CD Let |z1−z2|=4,|z3,z4|=10 and the diagonals AC and BD intersects at P. It is given that Arg(z4−z2z3−z1)=π2 and Arg(z3−z2z4−z1)=π4
Which of the following option(s) is/are incorrect?
Value of |CP−DP| is equal to 10√21
PB:PD=2:5
PC:AC=5:7
PC:AC=2:3
The correct Answer is:D
ΔABP and ΔCDP are similar if AP=2x
BP=2y then CP=5x,DP=5y
Area of trapezium ABCD=492xy
tanα=2x5y,tanβ=2y2x also α+β=45∘
⇒xy=1021(x2+y2)
Also AB2=AP2+BP2⇒x2+y2=4⇒xy=4021
Ar(ΔPCD)=5xy
Similar Questions
Let A(z1),B(z2),C(z3 and D(z4) be the vertices of a trepezium in an Argand plane such that AB∣∣CD Let |z1−z2|=4,|z3,z4|=10 and the diagonals AC and BD intersects at P. It is given that Arg(z4−z2z3−z1)=π2 and Arg(z3−z2z4−z1)=π4
Which of the following option(s) is/are correct?
View SolutionLet A(z1),B(z2),C(z3) be the vertices of an equilateral triangle ABC in the Argand plane, then the number z2−z32z1−z2−z3, is
View SolutionIf z1,z2andz3 are the vertices of a triangle in the argand plane such that |z1−z2|=|z1−z3|, then ∣∣∣arg(2z1−z2−z3z3−z2)∣∣∣ is
View SolutionIf z1,z2,z3 are the vertices of an equilational triangle ABC such that |z1−i|=|z2−i|=|z3−i|, then |z1+z2+z3| equals to
View SolutionIf A(z1), B(z2), C(z3) are vertices of a triangle such that z3=z2−iz11−i and |z1|=3, |z2|=4 and |z2+iz1|=|z1|+|z2|, then area of triangle ABC is
View SolutionIf A(z1),B(z2),C(z3) are the vertices of an equilateral triangle ABC, then arg 2z1−z2−z3z3_z2=
View SolutionIf z1z2,z3 and z4 taken in order vertices of a rhombus, then proves that Re(z3−z1z4−z2)=0
View SolutionIf z1,z2,z3,z4 are complex numbers, show that they are vertices of a parallelogram In the Argand diagram if and only if z1+z3=z2+z4
View SolutionIf |z1|=|z2| and arg (z1)+arg(z2)=0, then
View SolutionIf z1=1+2i,z2=2+3i,z3=3+4i, then z1,z2 and z3 represent the vertices of a/an.
View Solution
