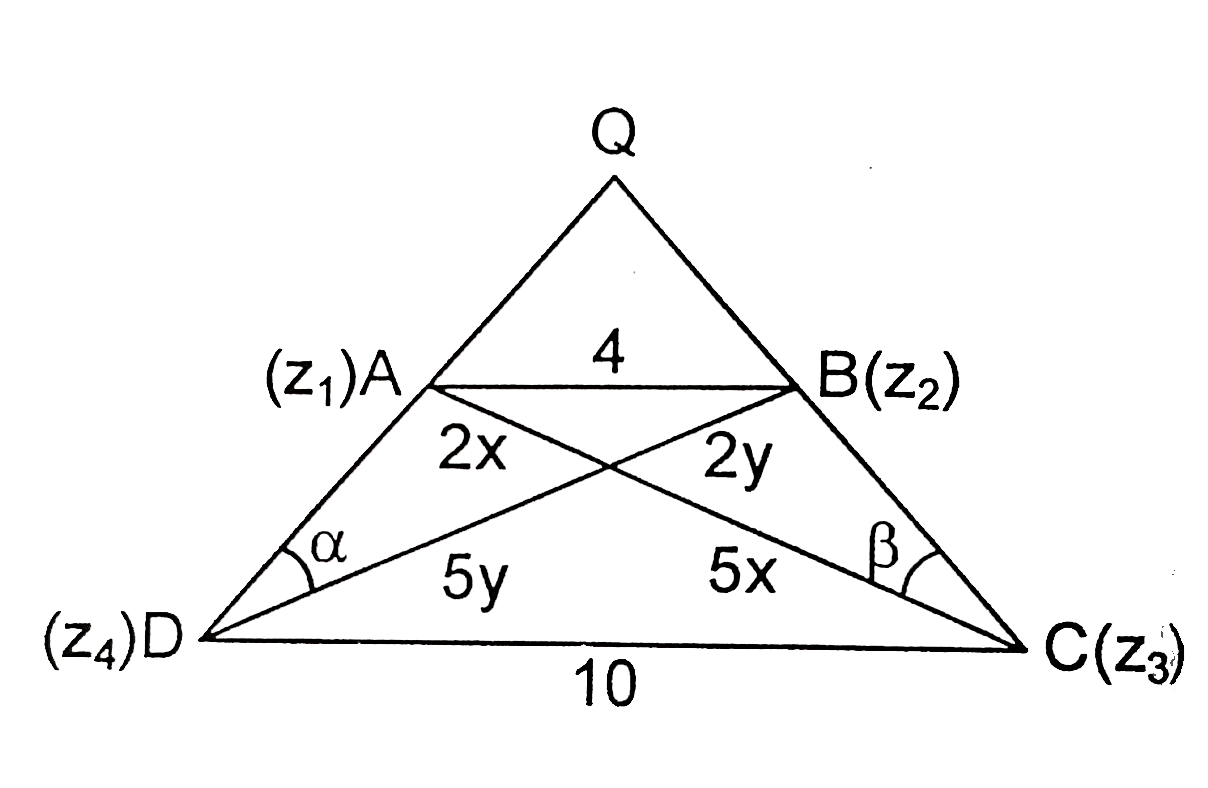
Let A(z1),B(z2),C(z3 and D(z4) be the vertices of a trepezium in an Argand plane such that AB∣∣CD Let |z1−z2|=4,|z3,z4|=10 and the diagonals AC and BD intersects at P. It is given that Arg(z4−z2z3−z1)=π2 and Arg(z3−z2z4−z1)=π4
Which of the following option(s) is/are correct?
Area of trepezium ABCD is equla to 1403 sq. units
Area of the trapezium ABCD is equal to 703 sq. units
Area of the triangle BCP is equal, to 10021 sq. units
Area of the triangle BCP is equal to 20042 sq. units
The correct Answer is:A
ΔABP and ΔCDP are similar if AP=2x
BP=2y then CP=5x,DP=5y
Area of trapezium ABCD=492xy
tanα=2x5y,tanβ=2y2x also α+β=45∘
⇒xy=1021(x2+y2)
Also AB2=AP2+BP2⇒x2+y2=4⇒xy=4021
Ar(ΔPCD)=5xy
Similar Questions
Let A(z1),B(z2),C(z3 and D(z4) be the vertices of a trepezium in an Argand plane such that AB∣∣CD Let |z1−z2|=4,|z3,z4|=10 and the diagonals AC and BD intersects at P. It is given that Arg(z4−z2z3−z1)=π2 and Arg(z3−z2z4−z1)=π4
Which of the following option(s) is/are incorrect?
View SolutionLet A(z1),B(z2),C(z3) be the vertices of an equilateral triangle ABC in the Argand plane, then the number z2−z32z1−z2−z3, is
View SolutionIf z1,z2andz3 are the vertices of a triangle in the argand plane such that |z1−z2|=|z1−z3|, then ∣∣∣arg(2z1−z2−z3z3−z2)∣∣∣ is
View SolutionIf z1,z2,z3 are the vertices of an equilational triangle ABC such that |z1−i|=|z2−i|=|z3−i|, then |z1+z2+z3| equals to
View SolutionIf A(z1), B(z2), C(z3) are vertices of a triangle such that z3=z2−iz11−i and |z1|=3, |z2|=4 and |z2+iz1|=|z1|+|z2|, then area of triangle ABC is
View SolutionIf A(z1),B(z2),C(z3) are the vertices of an equilateral triangle ABC, then arg 2z1−z2−z3z3_z2=
View SolutionIf z1z2,z3 and z4 taken in order vertices of a rhombus, then proves that Re(z3−z1z4−z2)=0
View SolutionIf z1,z2,z3,z4 are complex numbers, show that they are vertices of a parallelogram In the Argand diagram if and only if z1+z3=z2+z4
View SolutionIf |z1|=|z2| and arg (z1)+arg(z2)=0, then
View SolutionIf z1=1+2i,z2=2+3i,z3=3+4i, then z1,z2 and z3 represent the vertices of a/an.
View Solution