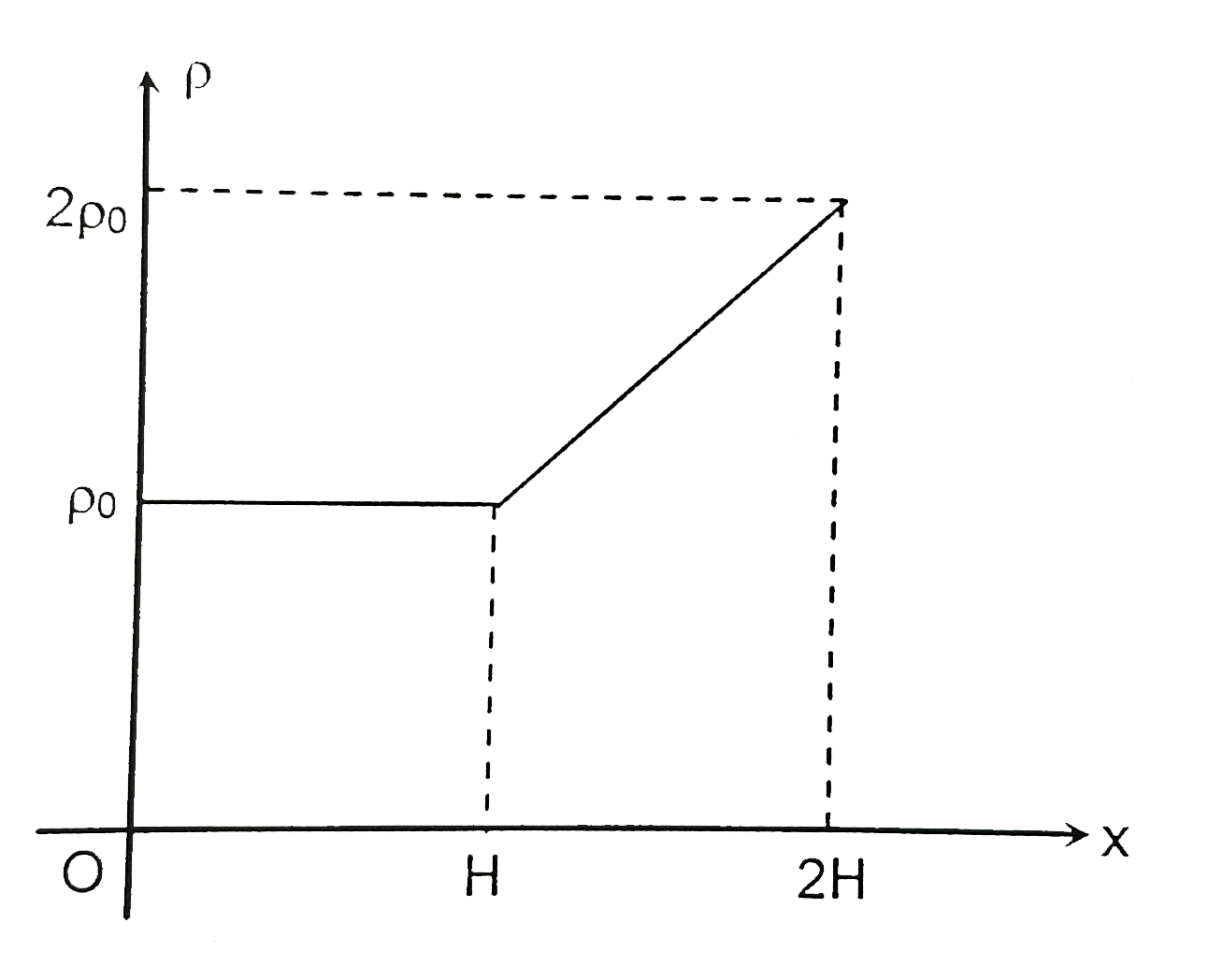
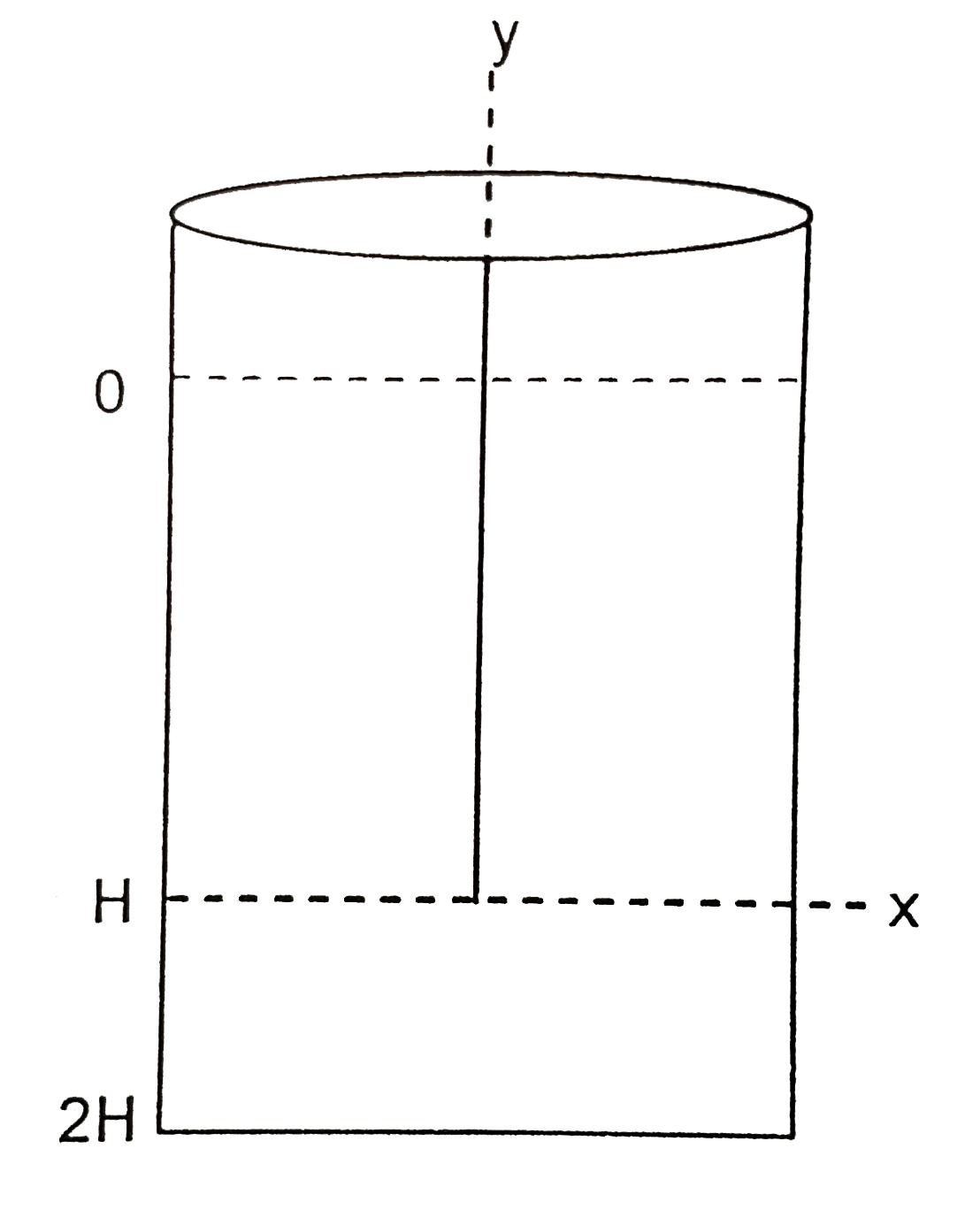
A large cylindrical container with open top contains a liquid upto height (2H=8m) and whose density varies as shown in the figure. Atmospheric pressure is 1 atm (=105N/m2)
Find the pressure at botom of cylindrical container in atm.
(given ρ0=103Kg/m2, and g=10m/s2)
The correct Answer is:2
We have to calculate the partial pressure, generated due the liquid of variable density
ρ=ρ0Hy+ρ0
W= weight of liquid column above the point A
⇒W=∫HySρgdy=gSρ0∫Hy(1+yH)dy
=gsρ0[(H−y)+H2−y22H]=Sρ0(H−y)(3H−y)g2H
P1= Patial pressure at interface (y=0) due to liquid with variable density =WS∣∣∣y=0
=3ρ0gH2
Πmplies Pressure at bottom =P0+P1+ρ0gH=ρ0+5ρ0gH2
=105+5×103×10×42=2×105=2 atm
Similar Questions
Water (ρ=103kg/m3) is filled in tube AB as shown in figure. (ω=10rad/s). Tube is open at end A. Atmospheric pressure is p0=105N/m2. Find absolute pressure at endB.
 .
.
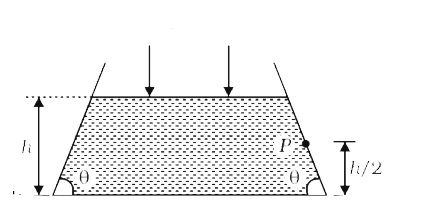
View SolutionA container (see figure) contains a liquid upto a height h. The density of the liquid is The gauge pressure at point P is ρghx. Find the value of x
View SolutionA cylindrical vessel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionA container filled with a liquid of density 4p as shown in the figure. The velocity efflux through orifice is (ρ is density of water and g = 10 ms−2)
_PHY_E05_013_Q01.png)
View SolutionWhat is the absolute pressure on a swimmer 10m below the surface of a lake? Take atmospheric pressure 1×105N/m2
View SolutionA cylindrical vessel of a very large cross sectional area is containing two immiscible liquids of density ρ1=600kg/m3 and ρ2=1200kg/m3 as shown in the figure.
A small hole having cross sectional area 5cm2 is made in right side vertical wall as shown. Take atmospheric pressure as p0=105N/m2,g=10m/s2. For this situation mark out the correct statement (s). Take cross sectional area of the cylindrical vessel as 1000cm2. Neglect the mass of the vessel.
View SolutionA square plate of side 10 m is placed horizontally 1 m below the surface of water. The atmospheric pressure is 1.013×105Nm−2. Calculate the total thrust on the plate.
(Density of water ρ=103kgm−3,g=9.8ms−2)
View SolutionThe pressure at a point in water is 10 N/m2. The depth below this point where the pressure becomes double is (Given density of water = 103 kg m−3, g = 10 m s−2)
View SolutionA siphon tube is discharging a liquid of density
900kgm3 as shown in figure. (P0=1.01×105N/m2)

Pressure at point B is
View SolutionA siphon tube is discharging a liquid of density
900kgm3 as shown in figure. (P0=1.01×105N/m2)
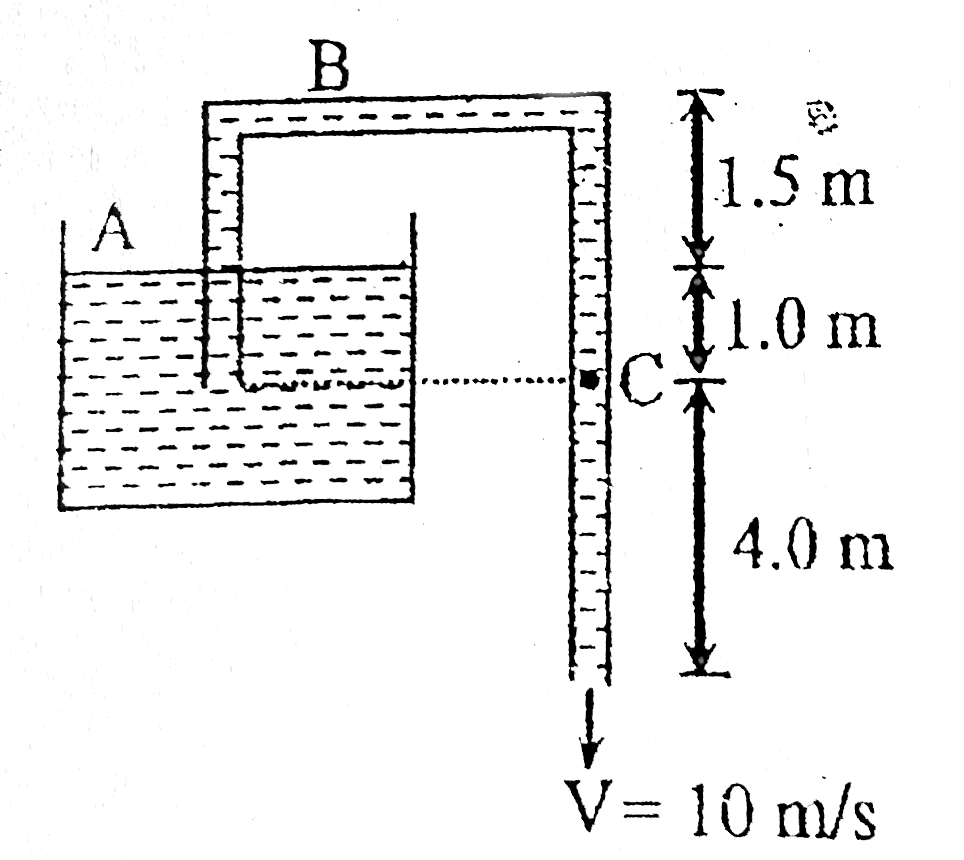
Pressure at point C is
View Solution
