A particle having charge 'q' and mass 'm' is projected with velocity (4ˆi−6ˆj+3ˆk)m/sec from the origin in a region occupied by electric field 'E' and magnetic field 'B' such that →B=B0ˆi and →E=E0ˆj (take qE0m=2). Find the time (in sec) when the magnitude of velocity of the charge particle becomes 5√5m/sec. (neglect the gravity)
The correct Answer is:8
To solve the problem, we need to analyze the motion of the charged particle under the influence of the electric and magnetic fields. The magnetic field does not do work on the particle, so we will only consider the effect of the electric field on the particle's velocity.
1. Identify the initial conditions:
- The initial velocity of the particle is given as:
→u=4^i−6^j+3^km/s
- The electric field is:
→E=E0^j
- The magnetic field is:
→B=B0^i
- Given that qE0m=2, we can denote the acceleration due to the electric field as:
ay=qE0m=2m/s2
2. Determine the change in the y-component of velocity:
- The y-component of the velocity changes due to the electric field. The equation of motion for the y-component is:
vy=uy+ayt
- Here, uy=−6m/s and ay=2m/s2. Thus, we have:
vy=−6+2t
3. Calculate the magnitude of the velocity:
- The total velocity vector is:
→v=vx^i+vy^j+vz^k
- The x-component vx and z-component vz remain unchanged since the magnetic field does not do work on the particle. Thus:
vx=4m/s,vz=3m/s
- The magnitude of the velocity is given by:
|→v|=√v2x+v2y+v2z
- We want this magnitude to equal 5√5m/s:
|→v|=5√5
4. Set up the equation for the magnitude:
- Substitute the known values into the magnitude equation:
5√5=√42+(−6+2t)2+32
- Squaring both sides gives:
125=16+(−6+2t)2+9
- Simplifying this, we have:
125=25+(−6+2t)2
100=(−6+2t)2
5. Solve for t:
- Taking the square root of both sides:
10=−6+2tor−10=−6+2t
- Solving the first equation:
2t=16⇒t=8s
- Solving the second equation:
2t=−4⇒t=−2s(not physically meaningful)
6. Final answer:
- The time when the magnitude of the velocity of the charged particle becomes 5√5m/s is:
t=8s
- The initial velocity of the particle is given as:
→u=4^i−6^j+3^km/s
- The electric field is:
→E=E0^j
- The magnetic field is:
→B=B0^i
- Given that qE0m=2, we can denote the acceleration due to the electric field as:
ay=qE0m=2m/s2
- The y-component of the velocity changes due to the electric field. The equation of motion for the y-component is:
vy=uy+ayt
- Here, uy=−6m/s and ay=2m/s2. Thus, we have:
vy=−6+2t
- The total velocity vector is:
→v=vx^i+vy^j+vz^k
- The x-component vx and z-component vz remain unchanged since the magnetic field does not do work on the particle. Thus:
vx=4m/s,vz=3m/s
- The magnitude of the velocity is given by:
|→v|=√v2x+v2y+v2z
- We want this magnitude to equal 5√5m/s:
|→v|=5√5
- Substitute the known values into the magnitude equation:
5√5=√42+(−6+2t)2+32
- Squaring both sides gives:
125=16+(−6+2t)2+9
- Simplifying this, we have:
125=25+(−6+2t)2
100=(−6+2t)2
- Taking the square root of both sides:
10=−6+2tor−10=−6+2t
- Solving the first equation:
2t=16⇒t=8s
- Solving the second equation:
2t=−4⇒t=−2s(not physically meaningful)
- The time when the magnitude of the velocity of the charged particle becomes 5√5m/s is:
t=8s
Similar Questions
A particle having mass m and charge q is released from the origin in a region in which ele field and magnetic field are given by B=−B0ˆjand E=E0ˆk.
Find the y- component of the velocity and the speed of the particle as a function of it z-coordinate.
View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are given by
→B=−B0→Jand→E−E0→K.
Find the speed of the particle as a function of its z-coordinate.
View SolutionA particle of spectfic charge α enters a uniform magnetic field B=−B0ˆk with velocity V=v0ˆi from the origin Find the time dependence of velocity and position of the particle
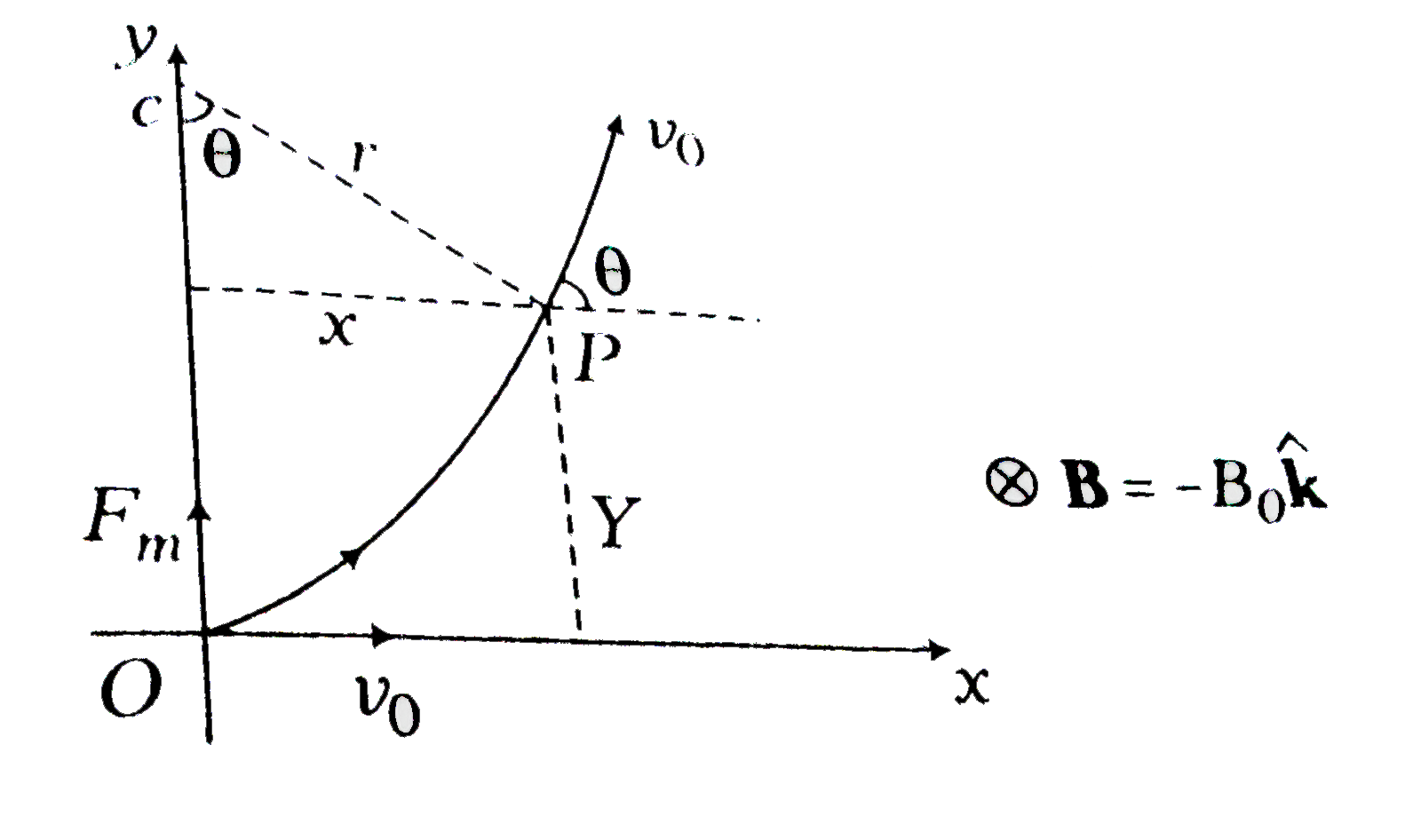
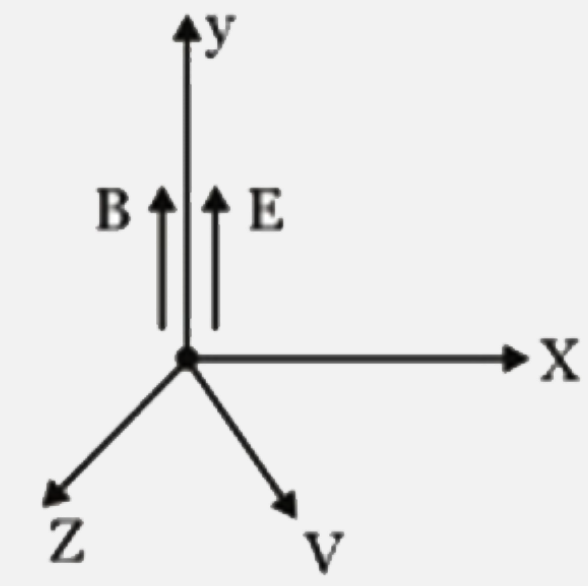
View SolutionA positive charge particle having change q and mass m has velocity →v=v(ˆi+ˆk√2) in the magnetic field B at the origin . Its speed as the function of y is :
View SolutionElectric field and magnetic field n a region of space is given by E=E0ˆj and B=B0ˆj. A particle of specific charge alpha is released from origin with velocity v=v0ˆi. Then path of particle
View SolutionA particle of specific charge alpha enters a uniform magnetic field B=−B0ˆk with velocity v=v0ˆi from the origin. Find the time dependence of velocity and position of the particle.

View SolutionA particle having charge q moves with a velocity v through a region in which both an electric field →E and a magnetic field B are present. The force on the particle is
View SolutionA particle is projected from ground with velocity 3ˆi+4ˆj m/s. Find range of the projectile :-
View SolutionA particle of charge q, mass starts moving from origin under the action of an electric field →E=E0ˆi and magnetic field →B=B0ˆk . Its velocity at (x,0,0) is v0(6ˆi+8ˆj). The value of is
View SolutionA particle of charge q, mass starts moving from origin under the action of an electric field →E=E0ˆi and magnetic field →B=B0ˆk . Its velocity at (x,0,0) is v0(6ˆi+8ˆj). The value of x is
View Solution
