A cylinder of mass M and radius R moves with constant speed v through a region of space that contains dust particles of mass m which is at rest. There are n number of particles per unit volume. The cylinder moves in a direction perpendicular to its axis. Assume m<<M, and assumes the particles do not interact wilth each other. All the collision takes place is perfectly elastic and the surface of the cylinder is smooth. The drag force per unit length of the cyliner require to maintain the speed v contant for the cylinder is K3nmRv2. Find the value of K?

The correct Answer is:8
In the frame of the heavy cylinder the particle comes in with speed V and then bounces off.
f=∫+π2−π22mvcos2θ(Rdθcosθ)lvn
fl=83mv2nR.

Similar Questions
A particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
View SolutionA body of mass 'm' moving with certain velocity collides with another identical body at rest. If the collision is perfectly elastic and after the collision both the bodies moves
View SolutionA particle of mass m, hits another particle in rest of mass m2, obliquely If both the particles after elastic collision moves perpendicular to each other then m1m2
View SolutionA particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in they y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to :
View SolutionTwo particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then

Speed of the particles after collision
View Solution(b) Two balls each of mass m moving in opposite direction with equal speed v collide head -on with each other . Predict the outcome of the collision assuming it perfectly elastic.
View SolutionA parallel beam of particles each of mass m moving with velocity v impinges on a wall at an angle θ to its normal. The number of particles per unit volume in the beam is n. If the collision of particles with the wall is elastic, then the pressure exerted by this beam on the wall is
View SolutionA particle of mass m strikes a disc of radius R and mass m with a speed u as shown in the figure. What is the speed of the particle just after the collision if the collision is perfectly inelastic ?
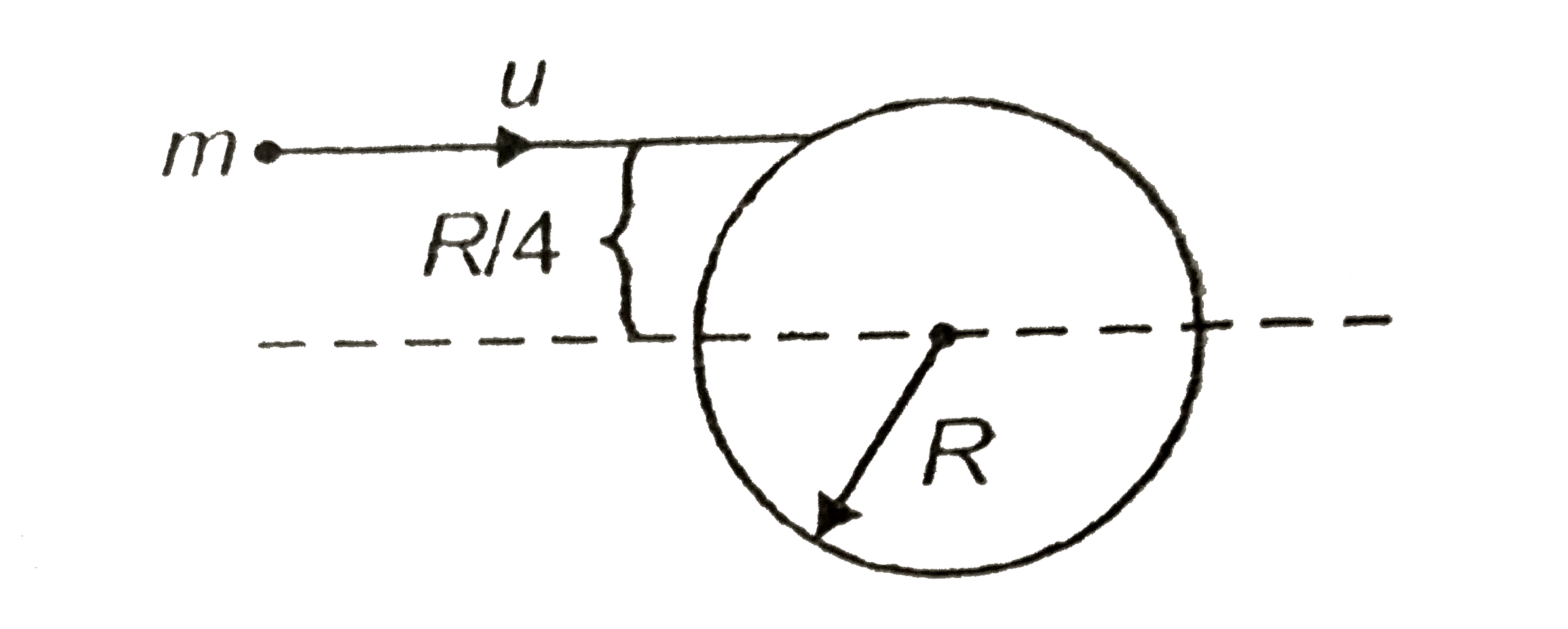
View SolutionFind the moment of inertia of a uniform cylinder about an axis through its centre of mass and perpendicular to its base. Mass of the cylinder is M and radius is R.
View SolutionA particle of mass m moves with constant speed v on a circular path of radius r. Find magnitude of average force on it in half revolution.
View Solution
