An RC− circuit, with R=600kΩ and C=10μF, is connected to a 5.0−V battery unit the capacitor is fully charged. Then, the battery is suddenly replaced with a new 3.00−V battery of opposite polarity. At what time after this replacement will the energy stored in the capacitor be zero ? (given that e≈83 )
12s
6s
3s
1.5s
The correct Answer is:B
To solve the problem, we need to determine the time at which the energy stored in the capacitor becomes zero after replacing the battery. Here’s the step-by-step solution:
Step 1: Understand the initial conditions
Initially, the capacitor is charged to a voltage of V0=5.0V with the capacitor fully charged. The energy stored in the capacitor can be expressed as:
U=12CV2
where C is the capacitance and V is the voltage across the capacitor.
Step 2: Determine the new voltage after battery replacement
After replacing the battery with a 3.0V battery of opposite polarity, the voltage across the capacitor changes. The new voltage V across the capacitor can be expressed as:
V=V0−Vnew=5.0V−(−3.0V)=5.0V+3.0V=8.0V
This means that the capacitor will now start discharging from 8.0V.
Step 3: Determine the time constant τ
The time constant τ for an RC circuit is given by:
τ=R⋅C
where R=600kΩ=600,000Ω and C=10μF=10×10−6F. Thus,
τ=600,000Ω×10×10−6F=6seconds
Step 4: Write the voltage equation over time
The voltage across the capacitor as it discharges can be expressed as:
V(t)=Vfinal+(Vinitial−Vfinal)e−t/τ
In this case, Vinitial=8.0V and Vfinal=−3.0V. Therefore,
V(t)=−3.0+(8.0−(−3.0))e−t/τ=−3.0+11.0e−t/6
Step 5: Set the voltage to zero to find the time
To find the time when the energy stored in the capacitor is zero, we set V(t)=0:
0=−3.0+11.0e−t/6
Rearranging gives:
11.0e−t/6=3.0
Dividing both sides by 11.0:
e−t/6=3.011.0
Step 6: Solve for t
Taking the natural logarithm of both sides:
−t/6=ln(3.011.0)
Thus,
t=−6ln(3.011.0)
Step 7: Calculate t
Using the approximation e≈83:
t=−6ln(3.011.0)≈6⋅1=6seconds
Final Answer
Thus, the time after the replacement when the energy stored in the capacitor becomes zero is:
6seconds
Initially, the capacitor is charged to a voltage of V0=5.0V with the capacitor fully charged. The energy stored in the capacitor can be expressed as:
U=12CV2
where C is the capacitance and V is the voltage across the capacitor.
After replacing the battery with a 3.0V battery of opposite polarity, the voltage across the capacitor changes. The new voltage V across the capacitor can be expressed as:
V=V0−Vnew=5.0V−(−3.0V)=5.0V+3.0V=8.0V
This means that the capacitor will now start discharging from 8.0V.
The time constant τ for an RC circuit is given by:
τ=R⋅C
where R=600kΩ=600,000Ω and C=10μF=10×10−6F. Thus,
τ=600,000Ω×10×10−6F=6seconds
The voltage across the capacitor as it discharges can be expressed as:
V(t)=Vfinal+(Vinitial−Vfinal)e−t/τ
In this case, Vinitial=8.0V and Vfinal=−3.0V. Therefore,
V(t)=−3.0+(8.0−(−3.0))e−t/τ=−3.0+11.0e−t/6
To find the time when the energy stored in the capacitor is zero, we set V(t)=0:
0=−3.0+11.0e−t/6
Rearranging gives:
11.0e−t/6=3.0
Dividing both sides by 11.0:
e−t/6=3.011.0
Taking the natural logarithm of both sides:
−t/6=ln(3.011.0)
Thus,
t=−6ln(3.011.0)
Using the approximation e≈83:
t=−6ln(3.011.0)≈6⋅1=6seconds
Thus, the time after the replacement when the energy stored in the capacitor becomes zero is:
6seconds
Similar Questions
A capacitor of capacitance C is initially charged to a potential difference of V volt. Now it is connected to a battery of 2V with oppoiste polarity. The ratio of heat generated to the final enegry stored in the capacitor will be
View SolutionA 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ?
View SolutionTwo capacitors of 10μF and 20μF are connected in series with a 30V battery. The charge on the capacitors will be, respectively
View SolutionThree capacitors C1=3μF,C2=6μFandC3=10μF are connected to a 50 V battery as shown in the figure below:
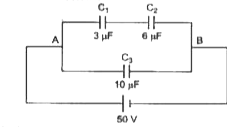
Calculate :
The charge on C1
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :
View SolutionWhen 20 V battery is connected to a circuit of capacitance (infinite ladder) as shown in the figure then charge supplied by the battery and total energy stored in the capacitors respectively are
_PHY_E05_063_Q01.png)
View SolutionAn Uncharged capacitor C is connected to a battery through a resistance R. Show that by the time the capacitor gets fully charged, the energy dissipated in R is the same as the energy stored in C.
View SolutionThe parallel combination of two air filled parallel plate capacitor of capacitance C and nC is connected to a battery of voltage, V. When the capacitors are fulley charged, the battery is removed and after that a dielectric material of dielectric constant K is placed between the two plates of the first capacitors. the new potential difference of the combined system is
View SolutionAt the trophic level of consumers, the rate at which food energy is assimilarted, is called ?
View Solution