Two highways are perpendicular to each other imagine them to be along the x-axis and the y-axis, respectively. At the instant t = 0, a police car P is at a distance d = 400 m from the intersection and moving at speed of 8 km//h towards it at a speed of 60 km//h along they y-axis. The minimum distance between the cars is
300m
240m
180m
120m
The correct Answer is:B
To solve the problem of finding the minimum distance between the two cars, we can follow these steps:
Step 1: Understand the scenario
We have two cars:
- Car A (the police car) is moving towards the intersection along the y-axis from a distance of 400 m at a speed of 80 km/h.
- Car B is moving along the x-axis at a speed of 60 km/h.
Step 2: Convert speeds to consistent units
Convert the speeds from km/h to m/s for easier calculations:
- Speed of Car A (VA) = 80 km/h = (80 * 1000 m) / (3600 s) = 22.22 m/s
- Speed of Car B (VB) = 60 km/h = (60 * 1000 m) / (3600 s) = 16.67 m/s
Step 3: Determine the relative velocity
To find the minimum distance, we need to analyze the relative motion of the two cars. The relative velocity of Car A with respect to Car B can be represented as:
- VAB=VA−VB
Since Car A is moving towards the intersection (in the negative y-direction) and Car B is moving towards the intersection (in the positive x-direction), we can consider:
- VA=−22.22^j (moving downwards)
- VB=16.67^i (moving right)
Step 4: Calculate the angle of approach
The angle θ between the paths of the two cars can be determined using the tangent function:
- tan(θ)=VBVA=16.6722.22
Step 5: Find the sine of the angle
Using the Pythagorean theorem, we can find the hypotenuse:
- Hypotenuse=√(V2A+V2B)=√(22.222+16.672)
Now calculate:
- V2A=493.83
- V2B=278.89
- Hypotenuse=√(493.83+278.89)=√772.72≈27.8
Now, we can find sin(θ):
- sin(θ)=VBHypotenuse=16.6727.8
Step 6: Calculate the minimum distance
The minimum distance dmin can be calculated using the formula:
- dmin=d⋅sin(θ)
Where d=400 m.
Now substituting the values:
- dmin=400⋅sin(θ)
Step 7: Final calculation
Using the value of sin(θ) calculated above, we can find dmin.
We have two cars:
- Car A (the police car) is moving towards the intersection along the y-axis from a distance of 400 m at a speed of 80 km/h.
- Car B is moving along the x-axis at a speed of 60 km/h.
Convert the speeds from km/h to m/s for easier calculations:
- Speed of Car A (VA) = 80 km/h = (80 * 1000 m) / (3600 s) = 22.22 m/s
- Speed of Car B (VB) = 60 km/h = (60 * 1000 m) / (3600 s) = 16.67 m/s
To find the minimum distance, we need to analyze the relative motion of the two cars. The relative velocity of Car A with respect to Car B can be represented as:
- VAB=VA−VB
- VA=−22.22^j (moving downwards)
- VB=16.67^i (moving right)
The angle θ between the paths of the two cars can be determined using the tangent function:
- tan(θ)=VBVA=16.6722.22
Using the Pythagorean theorem, we can find the hypotenuse:
- Hypotenuse=√(V2A+V2B)=√(22.222+16.672)
- V2A=493.83
- V2B=278.89
- Hypotenuse=√(493.83+278.89)=√772.72≈27.8
- sin(θ)=VBHypotenuse=16.6727.8
The minimum distance dmin can be calculated using the formula:
- dmin=d⋅sin(θ)
Where d=400 m.
- dmin=400⋅sin(θ)
Using the value of sin(θ) calculated above, we can find dmin.
Similar Questions
A car is moving on a straight road covers one third of the distance with a speed of 20 km/h and the rest with a speed of 60 km/h. The average speed of the car is
View SolutionThe straight roads intersect at an angle of 60°. A bus on one road is 2 km away from the intersection and a car on tire other road is 3 km away from the intersection. Then, the direct distance between the two vehicles, is
View SolutionA car covers a distance of 160 km between two cities in 4 h. What is the average speed of the car?
View SolutionA body starts from the origin with an acceleration of 6ms−2 along the x - axis and 8ms−2 along the y - axis. Find its distance from the origin after 4s.
View SolutionTwo roads interest at right angle , one goes along the x - axis, another along the y - axis. At any instant, two cars AbadB moving along yandx directions, respectively, meet at intersection. Draw the direction of the motion of car A as seen from car B.
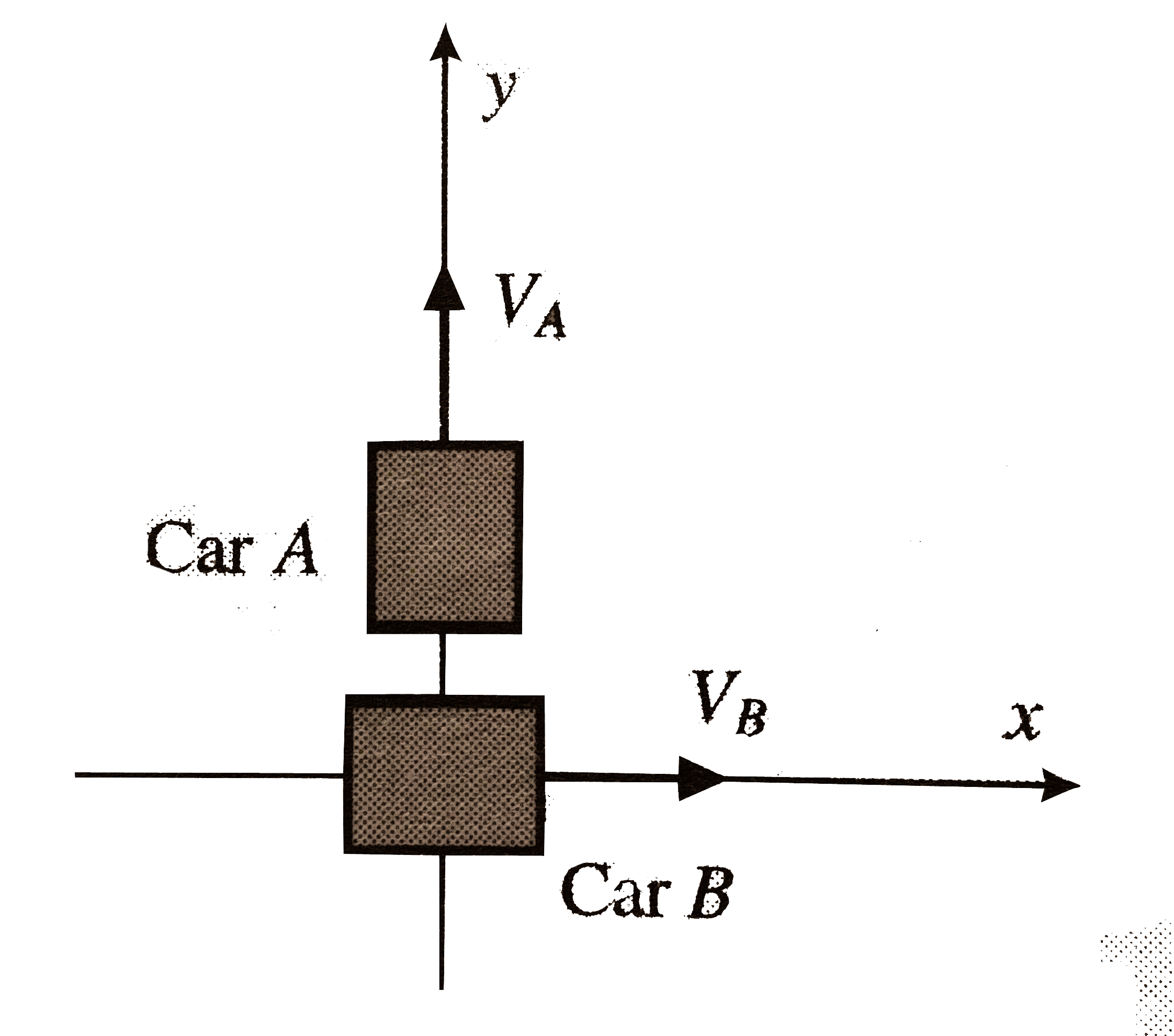 .
.
View SolutionA car moves a distance of 200m. It covers the first-half of the distance at speed 40km/h and the second-half of distance at speed vkm/h. The average speed is 48km/h. Find the value of v.
View SolutionA car moving with a speed of 40km/h can be stopped by applying the brakes after at least 2 m. If the same car is moving with a speed of 80km/h, what is the minimum stopping distance?
View SolutionA car moving with a speed of 40km/h can be stopped by applying the brakes after at least 2 m. If the same car is moving with a speed of 80km/h, what is the minimum stopping distance?
View SolutionA car moving with a velocity of 40 km/h can be stopped by brekes after travelling at least 5 m. If same car moves at a speed of 80 km/h the minimum stopping distance is
View SolutionA train covers the first half of the distance between two stations with a speed of 40 km/h and the other half with 60 km/h. Then its average speed is :
View Solution

