
All three spheres are identical having radius 10 cm. there is no slipping at any point of contact. Plank P and Q are moving in opposite direction with speed 10 and 30 cm/sec. height of instantaneous axis of rotation of sphere A from the gound is
20 cm
30 cm
15 cm
25 cm
The correct Answer is:D
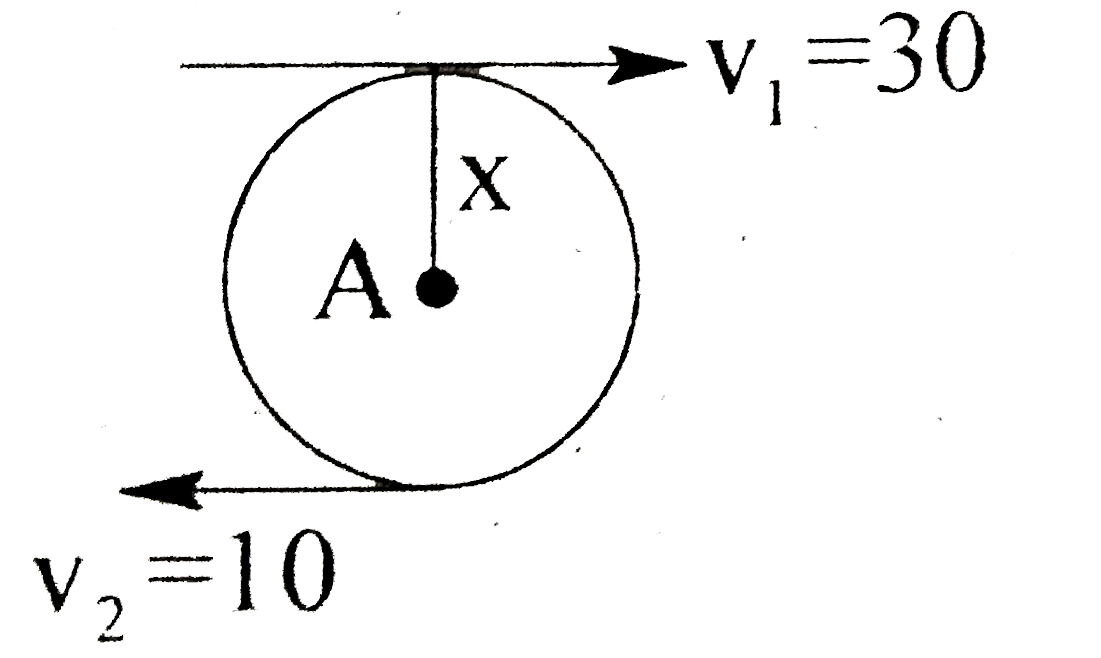
Let x be the surface distarice of axis of rotation from the top of sphere A (downward). Since angluar velocity of the top and bottom point of sphere A will be same, therefore,
ω=30x=10(2R−x)
30x=1020−x
⇒x=15
∴ Distance from ground
=2R+(2R−x)
=20+5=25cm
Similar Questions
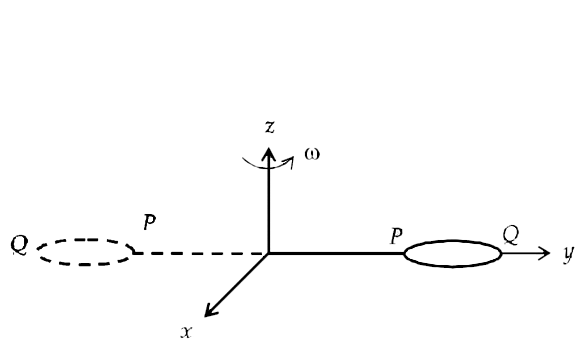
The general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case
Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of 45∘ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed ω about the z-axis.
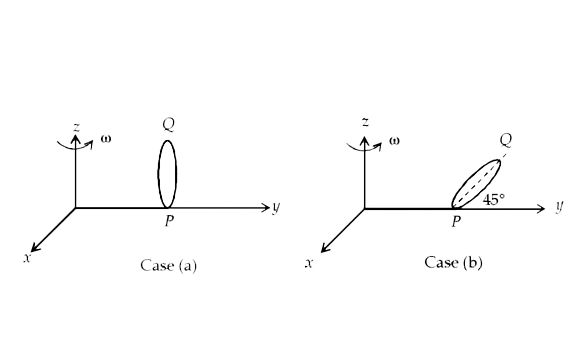
Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?
View SolutionA train is moving with a constant speed of 10m/s in a circle of radius 16πm. The plane of the circle lies in horizontal x-y plane. At time t = 0, train is at point P and moving in counter- clockwise direction. At this instant, a stone is thrown from the train with speed 10m/s relative to train towards negative x-axis at an angle of 37∘ with vertical z-axis . Find
(a) the velocity of particle relative to train at the highest point of its
trajectory.
(b) the co-ordinates of points on the ground where it finally falls and that of the hightest point of its trajectory. (Take g =10m/s2,sin37∘=35
View SolutionA circle of radius unity is centered at thet origin. Two particles tart moving at the same time from the point (1,0) and move around the circle in opposite direction. One of the particle moves anticlockwise with constant speed v and the other moves clockwise with constant speed 3v. After leaving (1,0), the two particles meet first at a point P, and continue until they meet next at point Q. The coordinates of the point Q are
View SolutionA wheel of radius R=10cm and moment of inertia I=0.05kgm2 is rotating about a fixed horizontal axis O with angular velocity ω0=10rads−1. A uniform riigid rod of mass m=3kg and length l=50cm is hinged at one end A such that it can rotate at end A in a vertical plane. End B of the rod is tied with a thread as shown in figure such that the rod is horizontal and is just in contact with the surface of rotating wheel. Horizontal distance between axis of rotation O of cylinder and A is equal to a=30cm.
If the wheel stops rotating after one second after the thread has burnt, calculate coefficient of friction ,μ between the rod and the surface of the wheel. (g=10ms−2)

View SolutionA small toy car moves round a circular track of radius 4 m. The car makes one revolution in 10 s. Calculate (a) the speed of the car, (b) its centripetal acceleration, (c) the centripetal force exerted,by the track if the.mass of the car is 200 g, (d) the safe speed with which the car can move around without toppling, if the distance between the wheels is 4 cm and the height of the centre of gravity of the car from the horizontal is 2 cm.
View SolutionTwo long parallel current carrying conductors 30 cm apart having current each of 10 A in opposite direction, then value of magentic field at a point of 10 cm between them, from any of the wire.
View SolutionTwo small spheres are attached to the ends of a long light nonconducting rod at a distance 40 mm from each other. All three spheres are nonconducting, have identical masses m=1g, and a positive charge q=1C is distributed evenly on the surface of each sphere. The whole system is placed on a horizontal frictionless nonconducting surface. Initially, all three spheres are at rest and the middle sphere is located a distance 30 mm from one of the ends of the rod and a distance 10 mm from the other. Find the maximum speed v (∈ms−1) of the middle sphere after the system is released.
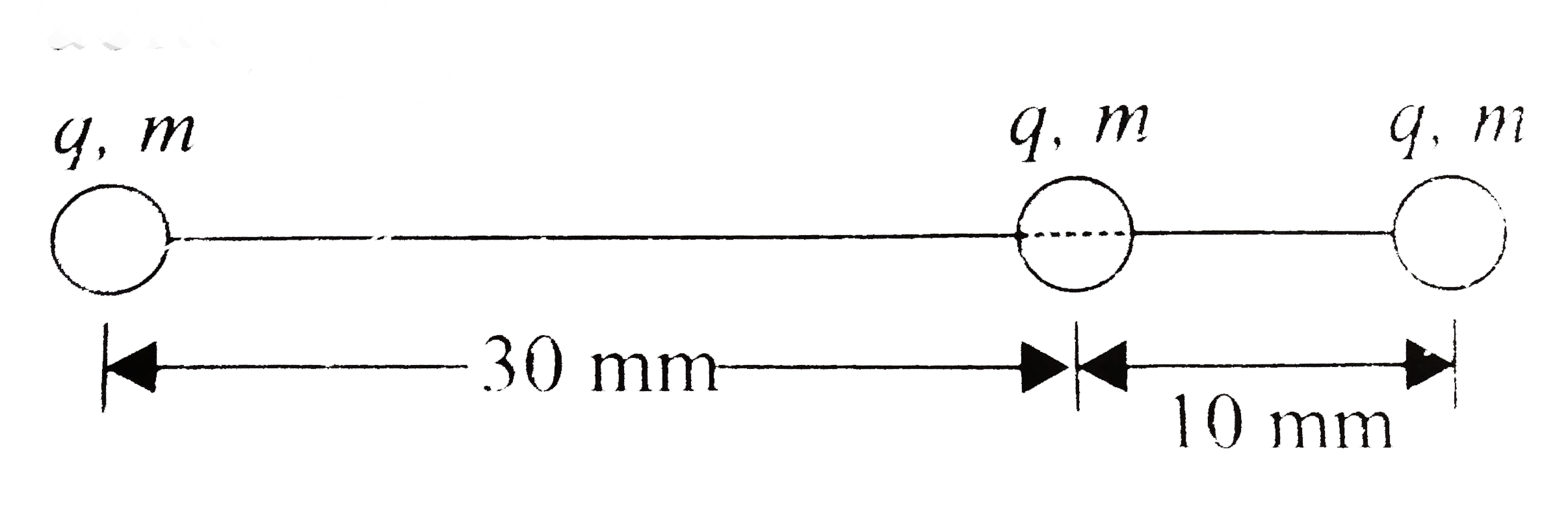
View SolutionA disc of radius 10 cm is rotating about its axis at an angular speed of 20 rad/s. Find the linear speed of
a. a point on the rim,
b. the middle point of the radius.
View SolutionTwo circular coils of wire each having a radius of 4cm and 10turns have a common axis and are 3cm apart If a current of 1A passes through each coil in the opposite direction find the magnetic induction
(i) At the center of either coil
(ii) At a point on the axis, midway between them .
View SolutionTwo circular coils of wire each having a radius of 4cm and 10turns have a common axis and are 3cm apart If a current of 1A passes through each coil in the opposite direction find the magnetic induction
(i) At the center of either coil
(ii) At a point on the axis, midway between them .
View Solution