Question

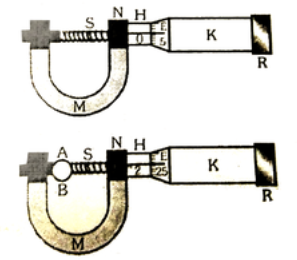
The diameter of a solid sphere is measured by varrier calipers (10 VSD =MSD) and (1MSD =1mm) the reading of main scale is 20 & varnier scale reading is 1. the volume of sphere will be

Options

A. `4.23cm^(3)`
B. `4.25cm^(3)`
C. `4.323cm^(3)`
D. `5.253cm^(3)`

Answer

B

Explanation

To find the volume of the solid sphere based on the measurements taken with the vernier calipers, we can follow these steps:

Step 1: Understand the Measurements
- The main scale reading (MSR) is given as 20 mm.
- The vernier scale reading (VSR) is given as 1.

Step 2: Calculate the Least Count of the Vernier Calipers
- Given that 10 Vernier Scale Divisions (VSD) = 1 Main Scale Division (MSD), and 1 MSD = 1 mm, we can calculate the least count (LC) as follows:

\( \text{Least Count (LC)} = \frac{1 \text{ MSD}}{10} = \frac{1 \text{ mm}}{10} = 0.1 \text{ mm} \)

Step 3: Calculate the Total Diameter of the Sphere
- The total diameter (D) can be calculated using the formula:

\( D = \text{MSR} + \text{VSR} \times \text{LC} \)

Substituting the values:

\( D = 20 \text{ mm} + 1 \times 0.1 \text{ mm} = 20 \text{ mm} + 0.1 \text{ mm} = 20.1 \text{ mm} \)

Step 4: Calculate the Radius of the Sphere
- The radius (R) of the sphere is half of the diameter:

\( R = \frac{D}{2} = \frac{20.1 \text{ mm}}{2} = 10.05 \text{ mm} \)

Step 5: Calculate the Volume of the Sphere
- The volume (V) of a sphere is given by the formula:

\( V = \frac{4}{3} \pi R^3 \)

Substituting the value of R:

\( V = \frac{4}{3} \pi (10.05 \text{ mm})^3 \)

Step 6: Calculate \(R^3\)
- First, we calculate \(R^3\):

\( R^3 = (10.05)^3 = 1015.507625 \text{ mm}^3 \)

Step 7: Substitute \(R^3\) into the Volume Formula
- Now substituting \(R^3\) into the volume formula:

\( V = \frac{4}{3} \pi (1015.507625) \approx \frac{4}{3} \times 3.14 \times 1015.507625 \)

Step 8: Calculate the Volume
- Performing the calculation:

\( V \approx \frac{4}{3} \times 3.14 \times 1015.507625 \approx 4270.36 \text{ mm}^3 \)

Step 9: Final Result
- The volume of the sphere is approximately \(4270.36 \text{ mm}^3\).

Summary
- The volume of the sphere is approximately \(4270.36 \text{ mm}^3\).