A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumedd to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall and the acceleration of the particle varies with x ( distance of the particle from the centre) according to
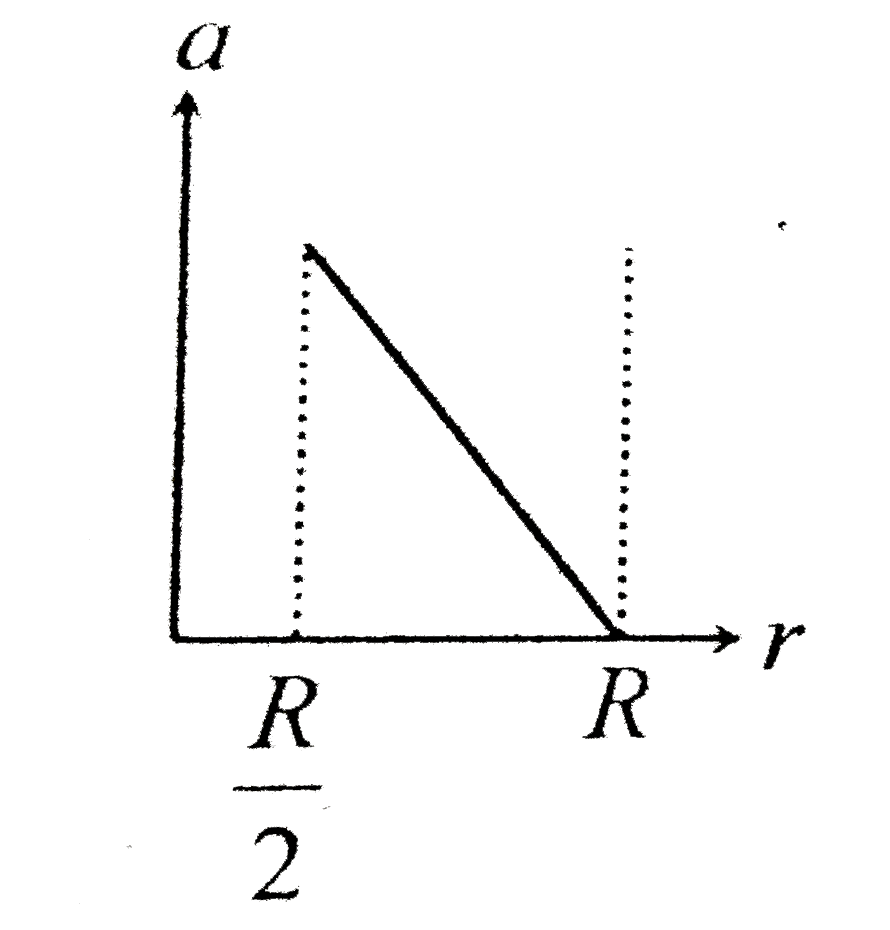

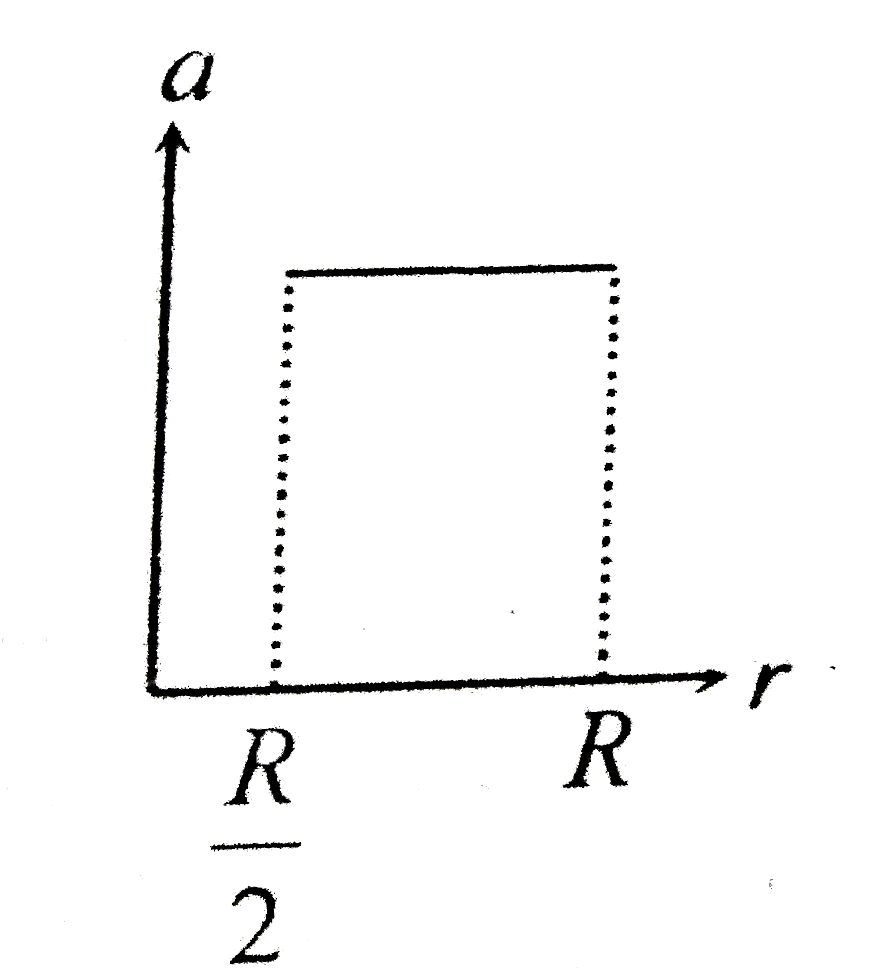
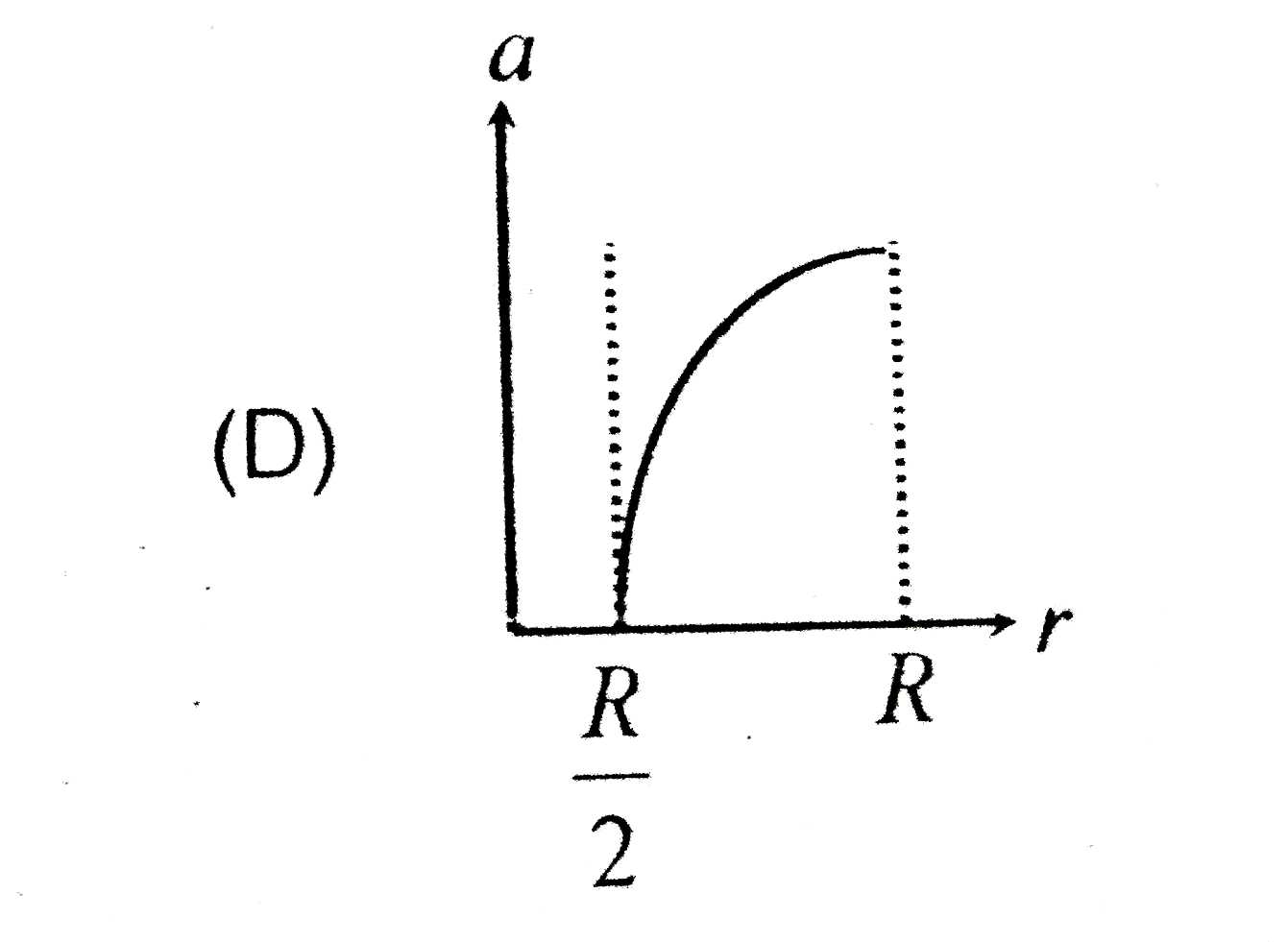
The correct Answer is:D

Let mass of the earth is Me and mass of object is m.
Force on object at A=(GMemR3r) towards centre
Force ono object along the tunnel =(GMeR3r)√r2−R24r
Acceleration of object along the tunnel =(GMeR3)√r2−R24
Similar Questions
A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall, and the acceleration of the particle vary with x (distance of the particle from the centre) according to
View SolutionA tunnel is dug along a chord of the earth a perpendicular distance R2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
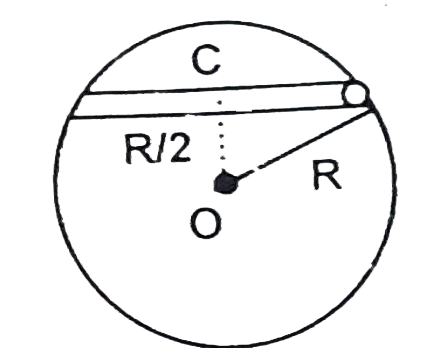
View SolutionA tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Maximum speed of the particle is
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Time period of the particle is not equal to
View SolutionA tunnel has been dug through the centre of the earth and a ball is released in it. It will reach the other end of the tunnel after
View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.

View SolutionA tunnel is dug along a diameter of the earth. Find the force in on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionSuppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point at a distance h directly above the tunnel. The motion of the particle as seen from the earth is
View SolutionThe distance of the centres of moon the earth is D. The mass of earth is 81 times the mass of the moon. At what distance from the centre of the earth, the gravitational force on a particle will be zero.
View Solution
